Introduction

TensorFlow is a popular open-source platform for developing machine learning models, and it has quickly become a go-to tool for developers and data scientists alike. One of the key features of TensorFlow is the ability to create sequential models that can be used for a variety of tasks, such as image classification or natural language processing.

In this article, we'll explore some of the core features of TensorFlow and explain how they work. Specifically, we'll cover the Sequential model, Dense layers, the compile method, the fit method, and the predict method. Let's dive in!

Sequential Model

The Sequential model is the most commonly used model in TensorFlow. It allows you to create a linear stack of layers, where each layer has a single input and output. To create a Sequential model, you simply instantiate the Sequential class:

 from tensorflow.keras.models import Sequential
model = Sequential()

Once you've created your Sequential model, you can add layers to it using the add method.

Dense layer

Dense layers are the most commonly used layer type in TensorFlow. They're fully connected layers, which means that each neuron in the layer is connected to every neuron in the previous layer. You can create a Dense layer using the Dense class:

 from tensorflow.keras.layers import Dense
layer = Dense(units=128, activation='relu', input_shape=(784,))

Here, we're creating a Dense layer with 128 units, a ReLU activation function, and an input shape of 784 (which corresponds to a flattened 28x28 image).

Compile Method

Once you've created your model and added layers to it, you need to compile it before you can train it. The compile method allows you to specify the optimizer, loss function, and metrics that you want to use. Here's an example of compiling a model:

 model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

In this example, we're using the Adam optimizer, categorical cross-entropy loss function, and accuracy as our metric.

Fit Method

After compiling your model, you can train it using the fit method. The fit method takes in your training data, along with the number of epochs (or iterations) that you want to run. Here's an example of fitting a model:

 history = model.fit(X_train, y_train, epochs=10, validation_data=(X_val, y_val))

In this example, we're fitting the model to our training data (X_train, y_train) for 10 epochs, and using our validation data (X_val, y_val) to evaluate the model after each epoch.

Predict Method

Finally, after training your model, you can use the predict method to make predictions on new data. The predict method takes in your test data and returns predictions for each input. Here's an example of using the predict method:

 y_pred = model.predict(X_test)

In this example, we're using our trained model to make predictions on our test data (X_test), and storing the predictions in y_pred.

MNIST

MNIST is a well-known dataset in the field of machine learning, particularly in the area of image classification. It stands for Modified National Institute of Standards and Technology, and it consists of a set of 70,000 grayscale images of handwritten digits (0-9), with each image having a resolution of 28x28 pixels.

The dataset is commonly used as a benchmark to test the accuracy and efficiency of various machine learning algorithms. The images are preprocessed and normalized to have values between 0 and 1, making it easier for machine learning models to learn from the data.

MNIST is often used as a starting point for beginners to learn about image classification and machine learning in general. It is also used as a baseline dataset for comparing the performance of new models and algorithms, as many state-of-the-art models have been tested on this dataset and achieved high levels of accuracy.

Import MNIST dataset

 # Load data from keras
fashion_mnist = tensorflow.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()

Lets start

The first layer is a flatten layer that takes in 28 by 28 pixel images, and converts them into a linear array. The second or middle layer is a hidden layer with 128 neurons or variables, which the network uses to create a complex function to classify images. Finally, the last layer has 10 neurons, one for each clothing class in the dataset, and produces a probability distribution over these classes.

The key to understanding this network is to think of the middle layer as a set of variables (x1, x2, x3, etc.) that can be combined in a weighted sum to produce an output value. This is similar to the equation y = w1x1 + w2x2 + ... + w128x128, where the weights (w1, w2, ..., w128) are learned by the network during training. When given an input image, the network calculates the values of these variables and uses them to produce a probability distribution over the clothing classes in the dataset.

 from keras.models import Sequential
from keras.layers import Flatten, Dense

# create a sequential model
model = Sequential()

# add a flatten layer to convert input images into a linear array
model.add(Flatten(input_shape=(28, 28)))

# add a hidden layer with 128 neurons and ReLU activation function
model.add(Dense(128, activation='relu'))

# add a final layer with 10 neurons and softmax activation function
model.add(Dense(10, activation='softmax'))

# compile the model with categorical cross-entropy loss and Adam optimizer
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

In this example, we create a sequential model and add a flatten layer with an input shape of 28 by 28. We then add a hidden layer with 128 neurons and a ReLU activation function, and a final layer with 10 neurons and a softmax activation function. Finally, we compile the model with categorical cross-entropy loss and Adam optimizer. This model can be trained and used to classify images of clothing into one of 10 classes.

To get a better understanding of the values in the MNIST dataset, we can print out a training image and its corresponding label. We can use the NumPy library to manipulate the data and Matplotlib to visualize the image. By experimenting with different indices in the array, we can see different examples of handwritten digits.

For example, we can print out the image and label at index 0 or 42 to compare two different images of boots. It's also important to note that the pixel values of the images are between 0 and 255, which is not optimal for training a neural network. Therefore, we normalize the pixel values by dividing them by 255.0, so they fall between 0 and 1, which will help the neural network learn better.

 import numpy as np
import matplotlib.pyplot as plt

# Print out a training image and its corresponding label
index = 0
np.set_printoptions(linewidth=320)
print(f'LABEL: {training_labels[index]}')
print(f'\nIMAGE PIXEL ARRAY:\n {training_images[index]}')
plt.imshow(training_images[index])

# Normalize the pixel values of the train and test images
training_images = training_images / 255.0
test_images = test_images / 255.0

In this example, we first set the index to 0 to print out the first training image and its corresponding label. We use NumPy's set_printoptions method to set the number of characters per row when printing, and then print out the label and pixel array of the image.

We then use Matplotlib's imshow method to visualize the image. Finally, we normalize the pixel values of the training and testing images by dividing them by 255.0, which scales the values to between 0 and 1.

This is the ouput :

 IMAGE PIXEL ARRAY:
 [[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0  82 187  26   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   1   0   0   1   0   0 179 240 237 255 240 139  83  64  43  60  54   0   1]
 [  0   0   0   0   0   0   0   0   0   1   0   0   1   0  58 239 222 234 238 246 252 254 255 248 255 187   0   0]
 [  0   0   0   0   0   0   0   0   0   0   2   3   0   0 194 239 226 237 235 232 230 234 234 233 249 171   0   0]
 [  0   0   0   0   0   0   0   0   0   1   1   0   0  10 255 226 242 239 238 239 240 239 242 238 248 192   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0 172 245 229 240 241 240 241 243 243 241 227 250 209   0   0]
 [  0   0   0   0   0   0   0   0   0   6   5   0  62 255 230 236 239 241 242 241 242 242 238 238 242 253   0   0]
 [  0   0   0   0   0   0   0   0   0   3   0   0 255 235 228 244 241 241 244 243 243 244 243 239 235 255  22   0]
 [  0   0   0   0   0   0   0   0   0   0   0 246 228 220 245 243 237 241 242 242 242 243 239 237 235 253 106   0]
 [  0   0   3   4   4   2   1   0   0  18 243 228 231 241 243 237 238 242 241 240 240 240 235 237 236 246 234   0]
 [  1   0   0   0   0   0   0   0  22 255 238 227 238 239 237 241 241 237 236 238 239 239 239 239 239 237 255   0]
 [  0   0   0   0   0  25  83 168 255 225 225 235 228 230 227 225 227 231 232 237 240 236 238 239 239 235 251  62]
 [  0 165 225 220 224 255 255 233 229 223 227 228 231 232 235 237 233 230 228 230 233 232 235 233 234 235 255  58]
 [ 52 251 221 226 227 225 225 225 226 226 225 227 231 229 232 239 245 250 251 252 254 254 252 254 252 235 255   0]
 [ 31 208 230 233 233 237 236 236 241 235 241 247 251 254 242 236 233 227 219 202 193 189 186 181 171 165 190  42]
 [ 77 199 172 188 199 202 218 219 220 229 234 222 213 209 207 210 203 184 152 171 165 162 162 167 168 157 192  78]
 [  0  45 101 140 159 174 182 186 185 188 195 197 188 175 133  70  19   0   0 209 231 218 222 224 227 217 229  93]
 [  0   0   0   0   0   0   2  24  37  45  32  18  11   0   0   0   0   0   0  72  51  53  37  34  29  31   5   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]]

Process finished with exit code 0

The MNIST dataset is split into two sets: training and testing. The training set is used to train the model, while the testing set is used to evaluate the model's accuracy on data that it hasn't seen before. This approach helps to prevent overfitting, where the model performs well on the training data but poorly on new, unseen data.

Designing the neural network model can seem daunting, but we can break it down into smaller concepts to make it more manageable. We can use various layers, such as Dense layers, to create a model that can classify the handwritten digits in the dataset. With a bit of practice, we can create complex models that achieve high accuracy on the MNIST dataset and similar image classification tasks.

Activation

The Rectified Linear Unit (ReLU) is an activation function used in neural networks that effectively passes values greater than 0 to the next layer in the network. The function returns x if x is greater than 0 and 0 if x is less than or equal to 0. This helps to introduce non-linearity into the model, making it more flexible and better able to learn complex patterns in the data.

The Softmax function is used in the output layer of a neural network to convert a set of values into a probability distribution. It takes a list of values and scales them so that the sum of all elements will be equal to 1. The scaled values can then be interpreted as the probability of each class. For example, in a classification model with 10 units in the output dense layer, the highest value at index = 4 indicates that the model is most confident that the input clothing image is a coat. If the highest value is at index = 5, then the model is most confident that the input image is a sandal, and so forth.

Callback

A common question that arises when experimenting with different numbers of epochs is how to stop training when a certain point is reached, without hard coding a specific number of epochs. Fortunately, the training loop in TensorFlow supports callbacks, which can be used to execute a code function after each epoch and check the metrics to determine whether to continue or cancel training.

To implement this, we first create a separate class in Python that contains the on_epoch_end function, which is called by the callback after each epoch and receives a logs object containing information about the current state of training. In the example code, the callback checks whether the loss is less than 0.4 and cancels training if it is.

Next, we instantiate the callback class and pass it to the callbacks parameter in the model.fit function to use during training. With this setup, we can dynamically stop training when a certain criteria is met, without needing to manually specify the number of epochs.

Here's an example of code that demonstrates how to use a callback to stop training:

 import tensorflow as tf

class StopTrainingCallback(tf.keras.callbacks.Callback):
    def on_epoch_end(self, epoch, logs={}):
        if(logs.get('loss') < 0.4):
            print("\nReached desired loss, cancelling training!")
            self.model.stop_training = True

# Instantiate the callback class
callbacks = StopTrainingCallback()

# Train the model and use the callback during training
model.fit(x_train, y_train, epochs=10, callbacks=[callbacks])

In this example, we create a class called StopTrainingCallback that implements the on_epoch_end function. This function checks if the current loss is less than 0.4 and sets the stop_training attribute to True if it is.

We then instantiate the callback class and pass it to the callbacks parameter in the model.fit function. With this setup, the callback is used during training and will cancel training when the desired loss is reached.

let define a real example :

 # Remember to inherit from the correct class
class myCallback(tf.keras.callbacks.Callback):
        # Define the correct function signature for on_epoch_end
        def on_epoch_end(self, epoch, logs={}):
            if logs.get('accuracy') is not None and logs.get('accuracy') > 0.99:                 
                print("\nReached 99% accuracy so cancelling training!")
                
                # Stop training once the above condition is met
                self.model.stop_training = True

Now should be able to link this to our code to interprate the callback during a training :

 #Build the classification model
#The first layer is a flatten layer for the images
#Last neuronal has 10 neuronal because we have 10 categories
def build_model():# Instantiate class
    callbacks = myCallback()
    model = keras.Sequential([
        keras.layers.Flatten(input_shape=(28,28)),
        keras.layers.Dense(128, activation=tensorflow.nn.relu),
        keras.layers.Dense(10, activation=tensorflow.nn.softmax),
    ])

    model.compile(optimizer=tensorflow.optimizers.Adam(),
                  loss='sparse_categorical_crossentropy',
                  metrics=['accuracy'])

    model.fit(train_images, train_labels, epochs=5, callbacks=[callbacks])
    return model

This should be the result of our model :

 Epoch 1/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.2568 - accuracy: 0.9260
Epoch 2/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.1136 - accuracy: 0.9672
Epoch 3/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0795 - accuracy: 0.9755
Epoch 4/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0575 - accuracy: 0.9828
Epoch 5/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0456 - accuracy: 0.9860
Epoch 6/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0357 - accuracy: 0.9890
Epoch 7/10
1872/1875 [============================>.] - ETA: 0s - loss: 0.0272 - accuracy: 0.9919
Reached 99% accuracy so cancelling training!
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0272 - accuracy: 0.9919

Convolutions and pooling

If you've ever worked with image processing, you might have come across the term convolution It's a technique that involves passing a filter over an image to highlight certain features. Convolutional neural networks (CNNs) use convolutions as a key component to classify images with high accuracy.

In the context of CNNs, convolutions work by sliding a filter (also known as a kernel) over the image and performing a dot product between the filter and the pixels in the current region. This process is repeated for each pixel in the image, creating a new image that highlights certain features. The filter acts as a set of weights that the network learns during training, making it possible to identify patterns in the data that are relevant for classification.

But how exactly does convolution work? Let's take a closer look.

First, we define the size of the filter. A common size is 3x3, which means that the filter is a 3x3 matrix of values. For each pixel in the image, we create a corresponding 3x3 grid by including the pixel's immediate neighbors. We then multiply each value in the grid by the corresponding value in the filter, and sum up the results. This gives us a new value for the pixel, which we can use to create a new image that highlights certain features.

For example, suppose we have an image of a shoe. We can apply a filter that detects vertical lines, which might be a relevant feature for classifying shoes. The filter might look like this:

 -1 0 1
-1 0 1
-1 0 1

When we apply this filter to the shoe image, we get a new image that highlights the vertical lines in the image. This can make it easier for the network to classify the image correctly.

Of course, filters can be more complex than this. They can be larger or smaller, and they can have different values that highlight different features. By applying multiple filters to an image, we can create a set of new images that each highlight different features. These new images can be used as input to the network, allowing it to identify a wider range of relevant patterns in the data.

But convolutions are just one part of the picture. Another important technique used in CNNs is pooling. Pooling involves taking small grids of pixels and selecting the maximum value in each grid. This has the effect of reducing the size of the image while preserving the relevant features that were highlighted by the convolutions.

For example, we might take a 2x2 grid of pixels and select the maximum value:

 [1 2]
[3 4]

In this case, we would select the value 4 as the maximum. This process is repeated for each grid of pixels, creating a new image that is smaller in size but still contains the relevant features from the original image.

Combined, convolutions and pooling create a powerful tool for image classification. By applying convolutions to an image, we can highlight the relevant features that are important for classification. By applying pooling, we can reduce the size of the image while preserving those features. This allows CNNs to classify images with high accuracy, making them a valuable tool for a wide range of applications.

Using tensorflow for convolution

In a previous example, we created a neural network that had an input layer shaped to our data, an output layer shaped to the number of categories we wanted to define, and a hidden layer in the middle. We used the Flatten function to turn our square 28 by 28 images into a one-dimensional array.

To add convolutions to our network, we need to modify our code. The last three lines are the same as before, with the Flatten, the Dense hidden layer with 128 neurons, and the Dense output layer with 10 neurons. What's different is what we add on top of this.

Let's go through the code line by line:

 model.add(Conv2D(64, (3,3), activation='relu', input_shape=(28,28,1)))

Here, we're specifying the first convolution. We're asking Keras to generate 64 filters for us. These filters are 3 by 3, their activation is relu (which means the negative values will be thrown away), and the input shape is the same as before, 28 by 28. The extra "1" means that we are using a single byte for color depth since our image is grayscale.

We can summaries:

These are the parameters:

• The desired number of convolutions to generate, preferably a power of 2 starting from 32, although the choice is arbitrary.
• The size of the convolution, which is a 3x3 grid in this instance.
• The chosen activation function, which in this case is ReLU. This function returns x if x is greater than 0, and 0 otherwise.

Additionally, the shape of the input data is specified for the first layer.

 model.add(MaxPooling2D(2,2))

Next, we add a MaxPooling layer. This reduces the dimensionality of the output from the previous layer, making it easier to process. The 2 by 2 parameter specifies the size of the pooling window.

 model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dense(10, activation='softmax'))

Finally, we add the same Flatten, Dense hidden layer, and Dense output layer as before. The Flatten function turns our output into a one-dimensional array, the Dense hidden layer has 128 neurons with a relu activation function, and the Dense output layer has 10 neurons with a softmax activation function.

You might be wondering what the 64 filters are and how they're generated. It's beyond the scope of this class to go into too much detail, but the filters are not random. They start with a set of known good filters in a similar way to the pattern fitting that we saw earlier. The filters that work well are learned over time through a process called backpropagation.

Using tensorflow for pooling

In order to further optimize our CNN model, we can add additional convolutional and max-pooling layers to the network. After each max-pooling layer, the size of the image is reduced, making it easier for the network to process.

Using the model.summary method, we can inspect the layers of the model and see how the image is transformed through the convolutions. The output shape column may be initially confusing, but it's important to remember that the filter is a 3 by 3 filter. When scanning through an image from the top left, the first pixel that can be calculated is one that has all eight neighbors that a 3 by 3 filter needs. This means that a one pixel margin all around the image cannot be used, resulting in an output from the convolution that is two pixels smaller on x and y.

After each max-pooling layer, the image size is reduced by a factor of two. For example, a 26 by 26 image is reduced to 13 by 13 after the first max-pooling layer, and then to 5 by 5 after the second max-pooling layer. This results in a flattened layer with 1,600 elements, as opposed to the previous 784. The number of convolutions specified per image will impact this number, as well as the other parameters set when defining the convolutional 2D layers.

By experimenting with different parameters and numbers of convolutions, we can find the sweet spot where the model is more accurate while also training faster. The workbook provides an opportunity to try this out for ourselves.

Here is a full example:

 # Define the CNN model
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))

After the convolution layer, a MaxPool2D layer follows, which serves to compress the image while preserving the highlighted features. By specifying (2,2) for the MaxPool2D, the image size is reduced to a quarter of its original size. Essentially, this is done by creating a 2x2 array of pixels and selecting the largest one, thereby reducing 4 pixels to 1. This process is repeated across the entire image, resulting in a reduction of both the horizontal and vertical pixel count by half, effectively reducing the image to 25% of its original size. While the technical details of this process are beyond the scope of this discussion, the overall effect is to compress the image while retaining the key features highlighted by the convolution.

About overfitting

To explore the results further, you could try running the training for about 20 epochs. However, be aware that while the results may initially appear good, the validation results may decrease due to overfitting. Overfitting occurs when the network becomes too specialized in the training data and is less effective in interpreting new, unseen data. It's like only ever seeing red shoes in your life and being very good at identifying them. But when you see blue suede shoes, they may be confusing.

To visualize the convolutions and pooling, you can print the first 100 labels in the test set, such as index 0, 23, and 28, which are all the same value (i.e., 9), indicating that they are all shoes. By running the convolution on each image, you can identify common features between them that the dense layer is likely using to identify shoes based on this convolution/pooling combination.

ImageDataGenerator

So far, you have built an image classifier using a deep neural network and improved its performance by adding convolutions. However, the previous classifier was limited to a dataset of uniform images, such as staged clothing framed in 28 by 28 pixels. Now, let's consider a scenario where you have larger images with different sizes, aspect ratios, and varying subject locations, like images of horses and humans. Additionally, the earlier examples used a built-in dataset with pre-split training and test sets and available labels. However, in many cases, you'll need to handle data preparation yourself.

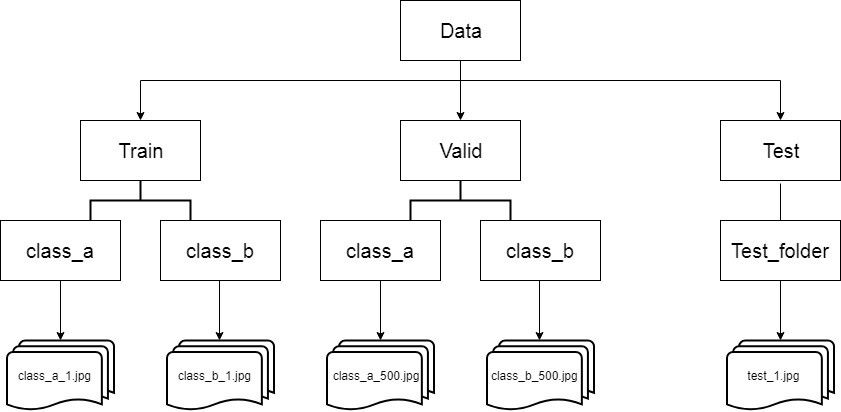
To address these challenges, TensorFlow provides useful APIs, such as the image generator in the Keras.preprocessing.image module. One notable feature of the image generator is its ability to automatically generate labels based on the directory structure. For example, consider a directory structure with an "images" directory containing sub-directories for training and validation. Within these sub-directories, you have "horses" and "humans" directories with respective images. The image generator can create a data feeder that loads and auto-labels the images accordingly. When pointing the image generator at the training directory, the labels will be "horses" and "humans," and the same will apply when pointing it at the validation directory.

Let's see an example of how to use the image generator in TensorFlow:

 from tensorflow.keras.preprocessing.image import ImageDataGenerator

# Instantiate the image generator
image_generator = ImageDataGenerator(rescale=1.0/255)

# Load and label images from the training directory
training_data_generator = image_generator.flow_from_directory(
    'path/to/training_directory',
    target_size=(300, 300),
    batch_size=32,
    class_mode='binary'
)

# Load and label images from the validation directory
validation_data_generator = image_generator.flow_from_directory(
    'path/to/validation_directory',
    target_size=(300, 300),
    batch_size=32,
    class_mode='binary'
)

We create an ImageDataGenerator object and specify rescale=1.0/255 to normalize the pixel values. Then, we use the flow_from_directory method to load and label images from the training and validation directories. It's important to note that when using flow_from_directory, you should point the generator at the directory containing the sub-directories with images, rather than directly at the sub-directory itself. The sub-directory names will be used as labels for the images contained within them.

To ensure consistent input sizes for training a neural network, the images will be resized to the specified target_size (in this case, 300 by 300 pixels) as they are loaded. This resizing is done automatically, so you don't need to preprocess the images separately.

The images will be loaded in batches, where the batch_size parameter determines the number of images in each batch. The choice of batch size can impact performance, but determining the optimal value is beyond the scope of this explanation.

Since this is a binary classifier (distinguishing between horses and humans), we set class_mode='binary. For multi-class classification, other options will be explored in later parts of the course.

The process for the validation generator is similar, except it points to the validation directory and generates labels accordingly.

In the provided notebook, you'll find instructions on how to download the images as a zip file, sort them into training and test sub-directories, and organize them into "horses" and "humans" sub-directories. These steps are implemented using pure Python and are not specific to TensorFlow or deep learning. The notebook will guide you through the process.

ConvNet to use complex images

Here's the code for the neural network used to classify horses versus humans, along with some explanations of the differences compared to the previous fashion item classifier:

 import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Conv2D(16, (3, 3), activation='relu', input_shape=(300, 300, 3)),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Conv2D(32, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(512, activation='relu'),
    tf.keras.layers.Dense(1, activation='sigmoid')
])

In this network, we have three sets of convolution and pooling layers at the top to handle the higher complexity and size of the images. Unlike the previous 28 by 28 images, we start with 300 by 300 images and gradually reduce their size through convolutions and pooling. The image size goes from 298 by 298 to 149 by 149, then to 73 by 73, and finally to 35 by 35. These convolutions help extract relevant features from the images.

The input shape of the network is set to (300, 300, 3), indicating that we expect color images with three channels (red, green, blue). Each channel is represented by one byte, resulting in a common 24-bit color pattern.

The output layer of the network has changed as well. Instead of having one neuron per class as in the previous multi-class classification, we now have a single neuron for the binary classification task of distinguishing between horses and humans. The activation function used is sigmoid, which is suitable for binary classification. It outputs a probability between 0 and 1, representing the likelihood of the input image belonging to one class or the other.

By resizing the images to 300 by 300 and using convolutions, we reduce the dimensionality of the data before feeding it into the dense layers. The final shape after flattening and convolutions is (78,400), which is significantly lower than the initial 90,000+ values if we had used the raw 300 by 300 images without convolutions. This reduction in dimensionality helps improve computational efficiency and allows the network to focus on relevant features.

You can experiment with different network architectures and parameters in the workbook to see how they affect the model's performance on the horses versus humans classification task.

training

When dealing with binary classification tasks, it's crucial to select appropriate loss functions and optimizers. In the example at hand, we move away from categorical cross entropy and instead opt for binary cross entropy. This choice aligns better with our binary classification problem, enabling more accurate model training and evaluation.

Furthermore, we introduce the RMSprop optimizer, which allows for fine-tuning the learning rate to experiment with performance improvements. While Adam optimizer was previously used, trying out different optimizers like RMSprop can help achieve better results depending on the specific task and dataset.

Understanding the Training Process

We encounter a slightly different training approach compared to the previous model.fit method. Instead, we utilize a generator, specifically an image generator, to stream and process the training data. Let's delve into the parameters involved and their significance.

1. Training Generator:

We employ a training generator to stream images from the training directory. Remember the batch size you set when creating the generator? It plays a vital role in the subsequent steps. For instance, if we set the batch size as 128 and have a total of 1,024 images in the training directory, we would load them in eight batches (128 images per batch).

2. Steps per Epoch:

To ensure all the images in the training directory are loaded during the training process, we need to set the steps_per_epoch parameter accordingly. In our example, this value would be eight, representing the number of batches required to cover all 1,024 images.

3. Number of Epochs:

Determining the appropriate number of epochs to train the model can be a complex task. In this case, we decide to use 15 epochs, which should be sufficient to capture the underlying patterns in the data and improve the model's performance.

4. Validation Set:

Validation plays a crucial role in evaluating the model's performance and preventing overfitting. The validation set, obtained from the previously created validation_generator, consists of 256 images. To handle them in batches of 32, we perform eight steps of validation during the training process.

Examining the Prediction Process:

After successfully training the model, the next logical step is to perform predictions on unseen data. Here's an example code snippet that illustrates this process:

1. Image Upload:

In this example, the code includes specific parts for Colab, facilitating the image upload process through a button. The uploaded images are stored in a list called "uploaded."

2. Preparing Images:

The loop iterates through the collection of images, enabling their loading and preparation for input into the model. It's essential to ensure that the image dimensions match the input dimensions specified during the model design phase.

3. Model Prediction:

To obtain predictions from the trained model, the code employs the model.predict function. By passing the image details as input, this function returns an array of classes. In the case of binary classification, the array will contain one item, with a value close to 0 for one class and close to 1 for the other.

Changing Image Size and Model Architecture

In the initial setup, our images were 300 by 300 pixels. However, we decide to reduce the image size to 150 by 150 pixels, which effectively reduces the dataset to a quarter of its original size. This change is made to observe the consequences it has on training and classification accuracy. Additionally, we make adjustments to the model architecture to accommodate the modified input shape. Specifically, we remove the fourth and fifth convolutional max pool combinations from the original architecture.

Training and Evaluation

After setting up the model with the modified architecture and image size, we proceed with training and evaluation. The training process shows promising results, with fast training and reasonably good accuracy and validation scores. It is worth noting that excessively high accuracy values, such as 1.000, can indicate overfitting, where the model performs exceptionally well on the training data but struggles with unseen data.

Evaluating Real-World Images

To further assess the model's performance, we test it with real-world images. The first image, featuring a girl and a horse, is still correctly classified as a horse. Similarly, another image of a horse is categorized accurately. Subsequently, images of other horses also receive correct classifications. However, a notable observation is made with an image of a woman. Previously, when using the larger 300 by 300 images and more convolutions, the model correctly classified her. However, with the reduced image size, the model misclassifies her. This demonstrates the importance of evaluating training data against a comprehensive validation set, identifying misclassifications, and exploring potential improvements.