Reinforcement learning

##Introduction In this article, we will explore reinforcement learning, which is a fundamental concept in the field of machine learning. Although it is not yet widely used in commercial applications, it has immense potential and is supported by extensive research that is constantly improving its capabilities. To illustrate this concept, let's take the example of an autonomous helicopter equipped with an onboard computer, GPS, accelerometers, gyroscopes, and a magnetic compass. The task is to write a program that allows the helicopter to fly autonomously using a reinforcement learning algorithm.

To do this, we first need to understand the concepts of "state" and "action". In reinforcement learning, the "state" of the system refers to the position, orientation, velocity, and other relevant information about the helicopter. On the other hand, "action" refers to the system's response to the current state. In the case of the helicopter, it is about how much to push the two control sticks to keep it balanced in the air and prevent it from crashing.

One approach to solving this problem is to use supervised learning, where a neural network can be trained using a dataset of states and the corresponding optimal action provided by an expert human pilot. However, this method is not ideal for autonomous helicopter flight, as it is difficult to obtain a large dataset of the exact optimal action for each state. Instead, reinforcement learning is used, which offers more flexibility in the design and training of the system.

In reinforcement learning, a "reward function" is used to train the system. Just as one would train a dog by praising it when it behaves well and correcting it when it misbehaves, a reward function is used to incentivize the system to behave well. In the case of the helicopter, a reward of plus one can be given for every second it flies well, while a negative reward is given for a bad flight, and a large negative reward for a crash.

Reinforcement learning is a powerful concept because it allows us to tell the system what to do rather than how to do it. This means that we can specify the reward function and let the algorithm automatically determine how to choose the optimal action in response to the current state. This approach has been successfully applied to various applications, such as robot control, factory optimization, financial trading, and games.

The Mars Rover

To illustrate the concept of reinforcement learning, we will use a simplified example inspired by the Mars rover. The example consists of a rover that can be in one of six positions, which we will call state 1 to state 6.

States and Rewards:

Each state has a different value, represented by a reward function. State 1 is the most valuable, with a reward of 100, and state 6 is less valuable, with a reward of 40. The rewards for all other states are zero as there is not as much interesting science to be done.

Robot Actions:

At each step, the rover can choose to move left or right from its current position. The rover can choose one of two actions: it can either go left or go right.

Robot Objectives:

The goal of the reinforcement learning algorithm is to maximize the reward that the rover receives. In other words, the rover must learn how to choose actions that will lead to the most valuable states.

Robot States and Transitions:

The position of the Mars rover is called the state in reinforcement learning. The rover can be in one of six states, and the rover starts in state 4. The state that the rover is in will determine the rewards that the rover receives when taking certain actions.

Robot Decisions:

The rover can make decisions on which direction to take based on the rewards associated with each state. For example, state 1 to the left has a very interesting surface that scientists would like the rover to sample. State 6 also has a fairly interesting surface that scientists would like the rover to sample, but not as much as state 1. 6. Robot learning: In reinforcement learning, algorithms use state, action, reward, and next state to decide which actions to take in each state, with the goal of maximizing the total reward obtained over time. By applying this concept to more complex tasks, such as controlling a helicopter or a robotic dog, we can create intelligent machines capable of learning from their environment and performing increasingly complex tasks.

In summary, the example of the Mars rover provides a simplified but illustrative example of the concepts of reinforcement learning. By teaching machines to make decisions based on rewards and states, we can create intelligent machines capable of learning from their environment and performing complex tasks.

The concept of return in reinforcement learning

Reinforcement learning involves taking actions that lead to different states and rewards. But how do we determine which set of rewards is better than another? This is where the concept of return comes in, which captures the value of rewards over time. In this section, we will explore the idea of return and its application in reinforcement learning.

The importance of return

When we take actions in a reinforcement learning system, the rewards received can vary significantly. However, we need to determine which set of rewards is more valuable. This is where the concept of return comes in, as it helps us capture the value of rewards over time.

To illustrate this concept, imagine that we have a five-dollar bill at our feet and a ten-dollar bill half an hour's walk away in a nearby town. While ten dollars is better than five dollars, it may not be worth walking half an hour to get it. Return helps us determine the value of rewards that can be obtained more quickly compared to those that take longer to achieve.

Understanding the formula for return

Return is the sum of rewards, weighted by the discount factor. This discount factor is a number slightly less than one, and it determines the value of rewards received at different times. A common discount factor value is 0.9, but it can range from 0 to 1.

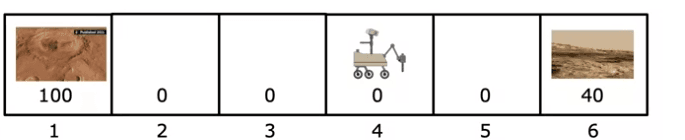
For example, consider a Mars Rover example where we start at state 4 and move to the left. The rewards we receive are 0, 0, 0, and 100 at the terminal state. If we set the discount factor to 0.9, we can calculate the return as follows:

Return = 0 + 0.9 * 0 + 0.9^2 * 0 + 0.9^3 * 100 = 72.9

The more general formula for calculating return is:

R_1 + Gamma * R_2 + Gamma^2 * R_3 + ... + Gamma^n * R_n

where R_n is the reward at step n and Gamma is the discount factor.

The impact of the discount factor

The discount factor has an impact on the value of return. The reinforcement learning algorithm becomes more impatient with a higher discount factor, as rewards received earlier are given more weight in the calculation of return. A common choice for the discount factor is 0.9 or 0.99, but this can vary depending on the application.

We can also set the discount factor to a value closer to 0, such as 0.5, which significantly reduces future rewards. In financial applications, the discount factor can represent the time value of money or interest rates.

Calculating returns for different states and actions

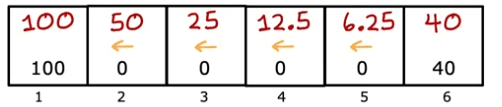
The return depends on the rewards received, which in turn depend on the actions taken. By taking different actions in different states, we can obtain different returns. For example, if we always go left, the return for state 4 is 12.5, but if we always go right, it is 10.

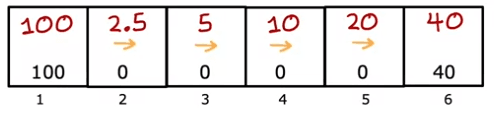
We can also choose actions based on the state we are in, such as going left in states 2 and 3 but going right in state 5. This yields different returns for each state, with state 1 having a return of 100, state 2 having a return of 50, and so on.

Negative rewards and discount factor

In systems with negative rewards, the discount factor encourages the system to push negative rewards as far into the future as possible. This is because future negative rewards are more heavily discounted than negative rewards in the present. This can be beneficial in financial applications where it is preferable to defer payments due to interest rates.

Making decisions

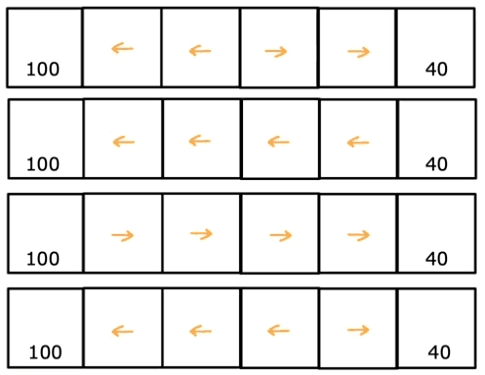
The goal is to find a policy, denoted Pi, that maps the current state of the agent to an action that maximizes the expected reward.

There are many ways to choose actions in reinforcement learning, such as always going for the closest reward or always going for the largest reward. To find the optimal policy, we need to take into account the current state of the agent, the actions it can take, and the rewards associated with those actions.

Return is an important concept in reinforcement learning, referring to the sum of rewards the agent receives, weighted by a discount factor. This factor encourages the agent to prioritize rewards that are closer in time, as they are weighted more heavily than rewards that are farther away.

A policy function Pi is used to map states to actions, and the goal of reinforcement learning is to find the optimal policy that maximizes the return. To achieve this, various algorithms can be used to iteratively update the policy based on the agent's experiences in the environment.

Markov Decision Process

The problem is formulated as a Markov Decision Process, or MDP for short, which includes states, actions, rewards, and a discount factor. The goal of the agent is to find a policy that maps states to actions in order to maximize the expected return, which is calculated using the rewards and discount factor.

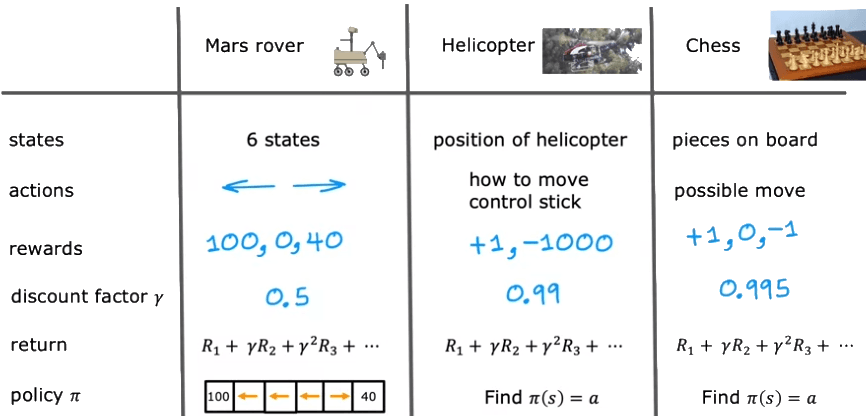
For example, in the case of a rover on Mars: The states are the six possible positions, the actions are the movements to the left or right, and the rewards are 100 for the farthest left state, 40 for the farthest right state, and zero in between, with a discount factor of 0.5.

Another example is the control of an autonomous helicopter, where the states are the possible positions, orientations, and velocities of the helicopter, the actions are the movements of the control sticks, and the rewards are plus one for a successful flight and minus 1,000 for a crash.

Similarly, in chess, the states are the positions of all pieces on the board, the actions are the legal moves, and the rewards are plus one for a win, minus one for a loss, and zero for a draw.

The formalism of the Markov decision process is named after the property that the future depends only on the current state and not on the past. In other words, the agent's decision considers only the current state and not how it got there. The agent chooses actions based on a policy, which is a function that maps states to actions. After taking an action, the agent observes the new state and associated reward, and the process repeats.

To develop an algorithm for choosing good actions, a key quantity is the state-action value function, which estimates the expected return from taking an action in a given state and then following a policy thereafter. The agent learns to compute this function and uses it to update its policy to improve its decision-making.

State-Action Value Function The state-action value function, denoted Q, is a function that takes as input a state and an action and provides a number that represents the return if the agent starts in that state, takes the specified action once, and then behaves optimally thereafter. The optimal behavior is the one that gives the highest possible return. It may seem strange that we need to compute Q when we already know the optimal policy, but we will see later how to resolve this circularity.

First, let's define the function Q more precisely. It is a function of the state-action pair (S, A) that gives the expected return if we start in state S, take action A, and then follow the optimal policy thereafter. Mathematically, we can write it as:

Q(S, A) = E[R | S, A], where R is the return, and E[R | S, A] represents the expected value of R given that we start in state S, take action A, and then follow the optimal policy. Note that R is a random variable that depends on the policy, so the expected value also depends on the policy.

Let's take an example. In the Mars Rover application with a discount factor of 0.5, the optimal policy is to go left from states 2, 3, and 4 and go right from state 5. To compute Q of S, A, we need to find the total return starting from state S, taking action A once, and then behaving optimally thereafter according to the policy. For example, if we are in state 2 and take the action of going right, we reach state 3 and then go left from state 3, and then left from state 2. Finally, we get a reward of 100. Therefore, Q of state 2 and going right is equal to the return, which is zero plus 0.5 times that plus 0.5 squared times that plus 0.5 cubed times 100, which is 12.5.

Similarly, in chess, the states are the positions of all pieces on the board, the actions are the legal moves, and the rewards are plus one for a win, minus one for a loss, and zero for a draw.

State-Action Value Function

The state-action value function, denoted Q, is a function that takes as input a state and an action and provides a number that represents the return if the agent starts in that state, takes the specified action once, and then behaves optimally thereafter. The optimal behavior is the one that gives the highest possible return. It may seem strange that we need to compute Q when we already know the optimal policy, but we will see later how to resolve this circularity.

Q(S, A) = E[R | S, A],

where R is the return, and E[R | S, A] represents the expected value of R given that we start in state S, take action A, and then follow the optimal policy. Note that R is a random variable that depends on the policy, so the expected value also depends on the policy.

Prenons maintenant un exemple. Supposons que nous avons un monde en grille simple avec quatre états : A, B, C et D. Chaque état a deux actions disponibles : monter ou aller à droite. Les récompenses sont les suivantes :

Monter depuis l'état A ou B donne une récompense de 0, et aller à droite donne une récompense de 1.
Monter ou aller à droite depuis l'état C donne une récompense de 5.
Monter ou aller à droite depuis l'état D donne une récompense de 10.

Le facteur de réduction est de 0,9, ce qui signifie que les récompenses futures sont réduites de 0,9 pour chaque pas de temps.

Nous pouvons calculer les valeurs Q pour chaque paire état-action comme suit. Commençons par l'état A et l'action haut. Si nous prenons cette action, nous finissons à nouveau à l'état A et recevons une récompense de 0. Le retour attendu est donc :

Q(A, haut) = E[R | A, haut] = 0 + 0,9 * Q(A, haut) + 0,1 * Q(B, haut), où le premier terme est la récompense immédiate, le deuxième terme est la récompense future actualisée si nous restons dans l'état A et prenons à nouveau l'action haut, et le troisième terme est la récompense future actualisée si nous passons à l'état B et prenons l'action haut là-bas. Nous pouvons écrire de manière similaire les valeurs Q pour les autres paires état-action :

Q(A, droite) = E[R | A, droite] = 1 + 0,9 * Q(B, droite) + 0,1 * Q(A, droite),
Q(B, haut) = E[R | B, haut] = 0 + 0,9 * Q(A, haut) + 0,1 * Q(C, haut),
Q(B, droite) = E[R | B, droite] = 1 + 0,9 * Q(C, droite) + 0,1 * Q(B, droite),
Q(C, haut) = E[R | C, haut] = 5 + 0,9 * Q(B, haut) + 0,1 * Q(D, haut),
Q(C, droite) = E[R | C, droite] = 5 + 0,9 * Q(D, droite) + 0,1 * Q(C, droite),
Q(D, haut) = E[R | D, haut] = 10 + 0,9 * Q(C, haut) + 0,1 * Q(D, haut),
Q(D, droite) = E[R | D, droite] = 10 + 0,9 * Q(D, droite) + 0,1 * Q(C, droite).

Nous pouvons résoudre ce système d'équations en utilisant des méthodes itératives ou l'inversion de matrice pour trouver les valeurs Q pour chaque paire état-action. Une fois que nous avons les valeurs Q, nous pouvons les utiliser pour déterminer la politique optimale, qui est l'action qui maximise la valeur Q pour chaque état. Dans ce cas, la politique optimale est la suivante :

À l'état A, prendre l'action droite.
À l'état B, prendre l'action droite.
À l'état C, prendre l'action haut.
À l'état D, prendre l'action haut.

Nous pouvons voir que cette politique correspond au choix de l'action ayant la valeur Q la plus élevée pour chaque état. Par exemple, dans l'état A, la valeur Q pour prendre l'action droite est de 1, ce qui est supérieur à la valeur Q pour prendre l'action haut (qui est 0). Par conséquent, la politique optimale est de prendre l'action droite à l'état A. Let's take another example. Suppose we have a simple grid world with four states: A, B, C, and D. Each state has two available actions: move up or move right. The rewards are as follows:

Moving up from state A or B gives a reward of 0, and moving right gives a reward of 1.
Moving up or moving right from state C gives a reward of 5.
Moving up or moving right from state D gives a reward of 10.

The discount factor is 0.9, which means that future rewards are discounted by 0.9 for each time step.

We can compute the Q-values for each state-action pair as follows. Let's start with state A and the action of moving up. If we take this action, we end up back at state A and receive a reward of 0. The expected return is therefore:

Q(A, up) = E[R | A, up] = 0 + 0.9 * Q(A, up) + 0.1 * Q(B, up),

where the first term is the immediate reward, the second term is the discounted future reward if we stay in state A and take the action up again, and the third term is the discounted future reward if we move to state B and take the action up there. We can write out the Q-values for the other state-action pairs in a similar fashion:

Q(A, right) = E[R | A, right] = 1 + 0.9 * Q(B, right) + 0.1 * Q(A, right),
Q(B, up) = E[R | B, up] = 0 + 0.9 * Q(A, up) + 0.1 * Q(C, up),
Q(B, right) = E[R | B, right] = 1 + 0.9 * Q(C, right) + 0.1 * Q(B, right),
Q(C, up) = E[R | C, up] = 5 + 0.9 * Q(B, up) + 0.1 * Q(D, up),
Q(C, right) = E[R | C, right] = 5 + 0.9 * Q(D, right) + 0.1 * Q(C, right),
Q(D, up) = E[R | D, up] = 10 + 0.9 * Q(C, up) + 0.1 * Q(D, up),
Q(D, right) = E[R | D, right] = 10 + 0.9 * Q(D, right) + 0.1 * Q(C, right).

We can solve this system of equations using iterative methods or matrix inversion to find the Q-values for each state-action pair. Once we have the Q-values, we can use them to determine the optimal policy, which is the action that maximizes the Q-value for each state. In this case, the optimal policy is as follows:

In state A, take the action right. In state B, take the action right. In state C, take the action up. In state D, take the action up. We can see that this policy corresponds to choosing the action with the highest Q-value for each state. For example, in state A, the Q-value for taking the action right is 1, which is higher than the Q-value for taking the action up (which is 0). Therefore, the optimal policy is to take the action right in state A.

In summary, the Q function allows us to compute the expected return for each state-action pair, which is essential for determining the optimal policy. In the example above, we used the Q function to find the optimal policy for a simple grid world. We can use similar techniques to solve more complex reinforcement learning problems.

Bellman

If you can calculate the Q-value function of S, A, you can determine the best action to take from any given state by selecting the action A that gives the largest Q-value of S, A. However, the question is how to calculate these Q-values of S, A? In reinforcement learning, the Bellman equation is a key equation that helps to calculate the Q-value function.

To explain the Bellman equation, let's rephrase the Bellman equation for the Q-value function in a slightly different way, which might make the math a bit clearer. Recall that Q(S,A) represents the expected cumulative reward if we start in state S, take action A, and then follow the optimal policy from that point onwards. Then, we can write the Bellman equation as follows:

Q(S,A) = E[R(S,A) + γ * max(Q(S', A'))],

where E[] represents expectation, R(S,A) is the immediate reward obtained when taking action A in state S, γ is the discount factor (which determines the weight to give to future rewards), max(Q(S', A')) represents the maximum expected cumulative reward that we can get from the next state S' by taking any possible action A', and Q(S', A') represents the expected cumulative reward if we start in state S', take action A', and then follow the optimal policy from that point onwards.

Now let's consider an example. Suppose we have a simple grid problem, where the agent can move up, down, left, or right, and each move has a reward of -1. There is also a special end state that has a reward of +10. The discount factor γ is set to 0.9. Here's a diagram of the grid:

 --------------
|  |  |  | 10|
--------------
|  | -1|  | -1|
--------------
|  |  |  | -1|
--------------
|  | -1|  | -1|
--------------

Let's assume that we want to calculate the Q-value for state (1,1) (i.e., the top-left corner) and the action "right". To do this, we apply the Bellman equation as follows:

Q(1,1,"droite") = E[R(1,1,"droite") + γ * max(Q(S', A'))]

= E[-1 + 0,9 * max(Q(1,2,"haut"), Q(2,1,"gauche"), Q(1,1,"bas"))]

= -1 + 0,9 * max(Q(1,2,"haut"), Q(2,1,"gauche"), Q(1,1,"bas")),

Where we used the fact that the immediate reward for moving to the right from state (1,1) is -1, and considered all possible states and actions.

Now, suppose we have already calculated the Q-values for all other states and actions. Here is a table of the Q-values we have calculated so far:

 ---------------------
|  | up | dwn| lft| rt |
---------------------
| 1|  6 |  7 |  5 |  ? |
---------------------
| 2|  1 |  ? |  2 |  6 |
---------------------
| 3|  0 |  1 |  1 |  1 |
---------------------
| 4|  ? |  2 |  ? |  2 |
---------------------

where we used the fact that the immediate reward for moving right from state (1,1) is -1, and considered all possible states and actions.

Now, suppose that we have already calculated the Q-values for all other states and actions. Here is a table of the Q-values we have calculated so far:

Note that the Q-value for state (1,1) and action "right" is currently unknown and is represented by "?". We want to use the Bellman equation to compute this Q-value. To do so, we first evaluate the Q-values for all possible states and actions:

Q(1,2,"up") = 7 Q(2,1,"left") = 1 Q(1,1,"down") = 5

Then, we substitute these values into the Bellman equation and obtain:

Q(1,1,"right") = -1 + 0.9 * max(7, 1, 5)

= -1 + 0.9 * 7

= 5.3.

Thus, the Q-value for state (1,1) and action "right" is 5.3. We can update our table accordingly:

 ---------------------
|  | up | dwn| lft| rt |
---------------------
| 1|  6 |  7 |  5 |  5.3 |
---------------------
| 2|  1 |  ? |  2 |  6 |
---------------------
| 3|  0 |  1 |  1 |  1 |
---------------------
| 4|  ? |  2 |  ? |  2 |
---------------------

We can repeat this process for all other unknown Q values until we have calculated the Q values for all states and actions.

In summary, the Bellman equation provides a way to compute Q values for all states and actions in a reinforcement learning problem, given rewards and the optimal policy. We can use this equation to iteratively update Q values until they converge to their true values. The iterative updating process of Q values is called value iteration, and it is one of the most common reinforcement learning algorithms.

Continuous State Space

When designing autonomous vehicles or other robotic systems, it is important to consider the state space in which the system operates. In the case of a rover on Mars, the state space is discrete and only includes six possible positions. However, for most robotic systems, the state space is continuous and can take any number of values within a given range.

For example, suppose we have a system that can move along a line, and its position is indicated by a number ranging from 0 to 1. This is an example of a continuous state space, because any number between 0 and 1 is a valid position for the system. In contrast, if the system could only be in one of two positions - let's say, 0 or 1 - then the state space would be discrete.

When working with vectors in continuous state spaces, each component of the vector can be represented using a real number. For example, if we have a system that can move in two dimensions, its state could be represented by a vector (x, y), where both x and y are real numbers. Any combination of real values for x and y within a valid range would be a valid state for the system.

In reinforcement learning, the state space is often used to represent the current state of the system, and the action space is used to represent the set of possible actions that the system can take. The goal of the reinforcement learning algorithm is to find an optimal policy - that is, a mapping between states and actions - that maximizes an objective function, such as the total reward obtained over time.

For example, suppose we have a robotic arm that can move in three dimensions. Its state could be represented by a vector (x, y, z), where x, y, and z are all real numbers representing the position of the arm in three-dimensional space. The action space could be represented by another vector (dx, dy, dz), where dx, dy, and dz are all real numbers representing the change in position of the arm in each dimension. The reinforcement learning algorithm would then attempt to find an optimal policy that maps each state to an action, in order to achieve a desired goal, such as reaching a particular location in space or avoiding obstacles.

Lunar Lander Simulation Example

Let's take an example : lunar lander

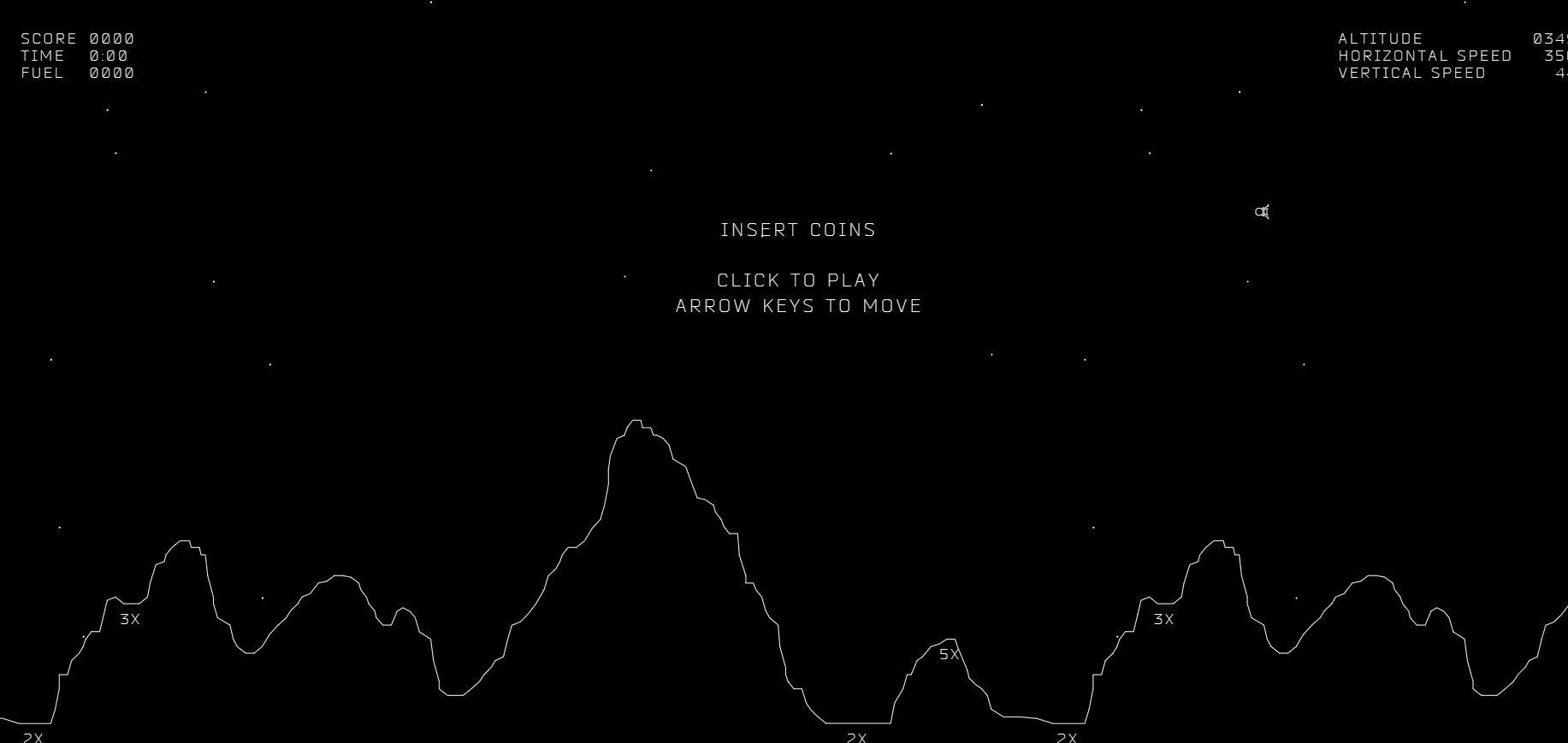
The Lunar Lander is a simulation that allows researchers to study reinforcement learning. It is similar to a video game, where you control a lunar lander that is rapidly descending towards the surface of the moon. Your goal is to safely land it on the landing pad by using the thrusters at the appropriate times.

Let's take a closer look at how the Lunar Lander simulation works. You control a lunar lander that is rapidly descending towards the surface of the moon. Your goal is to safely land it on the landing pad by using the thrusters at the appropriate times.

There are four possible actions in the simulation: "do nothing", "left", "main", and "right". If you do nothing, the lunar lander will be pulled towards the surface of the moon by the forces of inertia and gravity. If you use the left thruster, the lander will move to the right. If you use the right thruster, the lander will move to the left. If you use the main engine, the lander will push down.

The state vector of the lunar lander includes its position, velocity, angle, and whether the left or right leg is touching the ground. The position indicates the distance to the left or right and the height of the lander. The velocity indicates the speed at which the lander is moving in the horizontal and vertical directions. The angle indicates the tilt of the lander to the left or right. The variables l and r indicate whether the left or right leg is touching the ground, and they have a binary value and can only take on the values of zero or one.

The reward function of the simulation is designed to encourage desired behaviors by the designers and discourage those that they do not want. If the lander lands safely on the landing pad, it receives a reward between 100 and 140, depending on its performance. If the lander approaches the landing pad, it receives a positive reward, and if it moves away, it receives a negative reward. If there is a collision, the lander receives a large negative reward of -100. If there is a soft landing (i.e., no collision), it receives a reward of +100 for each leg on the ground. It also receives a reward of +10 for each leg on the ground, and finally, it receives a negative reward each time it uses the left or right lateral thrusters (-0.03) or the main engine (-0.3).

The goal of the Lunar Lander problem is to learn a policy π that selects the optimal action a for a given state s. The policy π must maximize the sum of discounted rewards, which is calculated using the gamma parameter. For the Lunar Lander simulation, a value of gamma of 0.985 is used. The learning algorithm used to find the optimal policy involves using deep learning or neural networks to approximate the optimal policy function. The learning algorithm iteratively updates the policy function based on observed states and rewards, using techniques such as Q-learning, policy gradient methods, or actor-critic methods. The goal is to find a policy that can successfully land the lunar lander on the landing pad with the highest possible total reward, while minimizing the use of fuel and avoiding collisions. The Lunar Lander problem is an exciting and challenging application of reinforcement learning, with many real-world applications such as robot control, autonomous driving, and gaming.

Learning the state-action function

Reinforcement learning is a type of machine learning in which an agent learns to make decisions by interacting with its environment. The agent receives rewards or punishments from the environment based on its actions, and it learns to maximize rewards over time by adjusting its behavior.

In the example of Lunar Lander, the agent is the neural network, and the environment is the Lunar Lander simulation. The goal of the agent is to learn a policy that tells it which action to take in each state to maximize its total reward. The policy is learned by estimating the state-action value function Q, which gives the expected total reward for taking a particular action in a particular state and following the optimal policy thereafter.

The key idea behind the reinforcement learning algorithm used in this example is to use the Bellman equations to create a set of state-action-reward-next state examples, and then train a neural network to approximate the state-action value function Q using supervised learning.

The Bellman equations are a set of recursive equations that relate the value of a state or state-action pair to the values of its neighboring states or state-action pairs. In the context of the Lunar Lander example, the Bellman equation for the state-action value function Q is:

Q(s,a) = R(s) + γ max_a' Q(s',a')

where s is the current state, a is the current action, R(s) is the immediate reward for taking action a in state s, γ is a discount factor that trades off immediate rewards for future rewards, s' is the next state, and max_a' Q(s',a') is the maximum expected reward for any action a' in the next state s'.

To train the neural network to approximate Q, we use the state-action-reward-next state tuples that we collect by interacting with the environment. Each tuple consists of a state-action pair (s,a), an immediate reward R(s), and the next state s'. We use these tuples to create a training set of input-output pairs (x,y) where x is the state-action pair and y is the target Q value calculated using the Bellman equation.

For example, suppose we have the following tuple:

s = [0.5, -0.2, 0.3, 0.7, 0.2, 1, 0, 1] a = [0, 1, 0, 0] r = 10 s' = [0.6, -0.1, 0.2, 0.6, 0.3, 1, 0, 1]

We would use this tuple to create a training example with randomly initialized parameters. We use a replay buffer to store the most recent experience tuples, which consist of the current state, the action taken, the reward obtained, and the next state. These experience tuples are used to create a training set of input-output pairs (x,y), where x is the state-action pair and y is the target Q value calculated using the Bellman equation.

To be more precise, the Bellman equation states that the Q value for a state-action pair (s,a) is equal to the immediate reward for that action plus the discounted maximum Q value for the next state (s') and all possible actions (a'). Mathematically, this can be written as:

Q(s, a) = r + γ * max(Q(s', a'))

where r is the immediate reward for action a in state s, γ (gamma) is a discount factor that determines the importance of future rewards, and max(Q(s', a')) is the maximum Q value for all possible actions a' in the next state s'.

During training, we use a replay buffer to randomly sample a batch of experience tuples (s, a, r, s') from the buffer and use them to update the Q network parameters. The goal is to minimize the difference between the predicted Q value and the target Q value, which is given by the Bellman equation.

To achieve this, we use a loss function that measures the mean squared error between the predicted Q value and the target Q value for each state-action pair in the batch. Mathematically, the loss function can be written as:

L = 1/N * Σ[(y - Q(s, a))^2]

where N is the batch size, y is the target Q value calculated using the Bellman equation, and Q(s, a) is the predicted Q value for the state-action pair (s, a).

The neural network is trained using gradient descent to minimize the loss function, and the Q network parameters are updated after each training iteration. By repeating this process with different batches of experience tuples, the Q network gradually learns to approximate the optimal Q function for the given task.

For example, in the case of the Lunar Lander problem, the Q network takes as input the current state of the lunar module and the possible actions, and returns the Q value for each action. During training, the Q network is updated using batches of experience tuples that consist of the current state, the action taken, the reward received, and the next state. Over time, the Q network learns to approximate the optimal Q function, which can be used to select the best action for the current state of the lunar module.

Greedy policy

The Q function is defined as Q(s, a) = E[R + γ maxa' Q(s', a')], where R is the immediate reward, γ is the discount factor, and s' is the resulting next state from taking action a in state s.

The goal of the learning algorithm is to estimate the Q function and learn the optimal policy that maximizes the expected cumulative reward. A common approach is to use a neural network to approximate the Q function, with the input being the state and action, and the output being the estimated Q value.

The Epsilon-greedy policy can be formalized as follows:

With probability Epsilon, select a random action. With probability 1 - Epsilon, select the action that maximizes the estimated Q value for the current state. For example, suppose we have a lunar lander environment with four possible actions: turn on the main thruster, turn on the left thruster, turn on the right thruster, and do nothing. If we set Epsilon to 0.1, then 10% of the time we will choose a random action, and 90% of the time we will choose the action with the highest estimated Q value.

Suppose the current state is such that the estimated Q values for the four actions are as follows: Q(s, main) = 0.5, Q(s, left) = 0.8, Q(s, right) = 0.6, and Q(s, none) = 0.2. With a probability of 0.9, we will choose the "left" action because it has the highest estimated Q value. With a probability of 0.1, we will choose a random action, which could be any of the four actions.

The choice of Epsilon is crucial for balancing exploration and exploitation. A high value of Epsilon means the agent will explore more and try new actions, which can be useful in the early stages of learning when Q values are not yet accurate. However, a low value of Epsilon means the agent will exploit current knowledge and choose the action that is expected to give the highest reward.

In practice, it is common to start with a high value of Epsilon and gradually decrease it over time as the agent learns more about the environment. This is often called an Epsilon-greedy annealing schedule. For example, we could start with Epsilon = 1.0 and decrease it slightly after each episode until it reaches a minimum value.

Limits of Reinforcement Learning

Reinforcement learning is an exciting technology that I am very interested in. However, there is often a lot of hype around reinforcement learning and its usefulness for practical applications. In this section, my goal is to provide a practical perspective on where reinforcement learning stands today.

One reason for the hype around reinforcement learning is that many research papers have focused on simulated environments. While these simulations can be useful for testing and prototyping, it is important to note that getting reinforcement learning algorithms to work in the real world can be much more difficult. This is particularly true for applications involving physical robots. Therefore, it is important to be mindful of this limitation and ensure that any reinforcement learning algorithm is tested and validated in the real world.

Despite the media coverage around reinforcement learning, it is also important to note that there are currently fewer practical applications of reinforcement learning than supervised and unsupervised learning. Therefore, if you are building a practical application, it is more likely that supervised or unsupervised learning will be the appropriate tool for the job. While reinforcement learning can be useful for some applications, it is not always the most appropriate approach.

Reinforcement learning remains one of the main pillars of machine learning, and it is an exciting research area with a lot of potential for future applications. By developing your own machine learning algorithms, integrating reinforcement learning as a framework can help you build more effective systems. While it can be difficult to get reinforcement learning algorithms to work in the real world, seeing your algorithms successfully perform a task such as safely landing a lunar lander on the moon can be a rewarding experience.