Introduction

When you visit online shopping sites like Amazon, movie streaming sites like Netflix, or food delivery apps, these sites recommend products, movies, or restaurants based on what they think you might like. For many businesses, recommendation systems generate a large portion of their sales, making the economy or value generated by these systems very important. This article will take a closer look at how recommendation systems work, using the application of predicting movie ratings as an example.

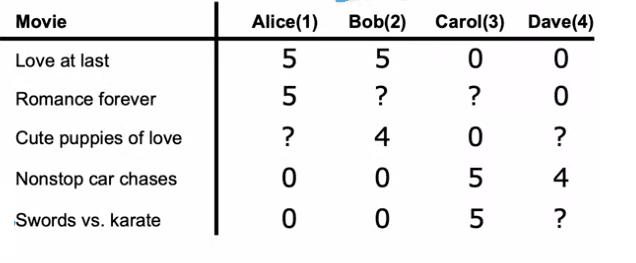
In a typical recommendation system, there is a set of users and a set of products that users can rate. For example, we have four users - Alice, Bob, Carol, and Dave - and five movies - Love at Last, Romance Forever, Cute Puppies of Love, Nonstop Car Chases, and Sword versus Karate.

We can say that:

• Nu: is the number of users
• Nm: is the number of movies

Users rate the movies on a scale of one to five stars, and in this example, we have users who have not yet rated certain movies. To know which users have rated which movies, we define r(i, j) as 1 if user j has rated movie i and 0 if they have not.

One approach to the problem of recommendation systems is to predict how users would rate movies they have not yet rated. Thus, the system can recommend movies to users that they are more likely to rate positively. However, to make these predictions, the system needs additional information about the movies, such as whether they are romantic or action movies. We will develop an algorithm to make these predictions in the next section, assuming we have access to this additional information.

It is important to note that the same logic behind recommendation systems can apply to recommending anything, from products to restaurants or even social media posts. The notation used in this article includes nu to denote the number of users and nm to denote the number of movies or articles. Additionally, y(i, j) is used to denote the rating given by user j for movie i, only if the movie has been rated.

Item Features

We will explore how to develop a recommendation system based on movie features. Specifically, we will examine a dataset containing four users and five movies, and assume that we have access to two features for each movie: X1, which measures the degree of romanticism of the movie, and X2, which measures the degree of action of the movie.

Let's start by defining the notation we will use throughout the article. We will use r(i,j) to indicate if user j rated movie i (r(i,j) = 1) or not (r(i,j) = 0). We will use y(i,j) to indicate the rating given by user j for movie i. We will use w(j) and b(j) to denote the parameters for user j, which we will learn using our recommendation system. Finally, we will use X(i) to denote the feature vector for movie i, which consists of X1 and X2.

To predict how a user j might rate a movie i based on the movie features X(i), we can use a linear regression model. Specifically, we can predict the rating as w(j).X(i)+b(j), where w(j) and b(j) are the parameters for user j.

To learn the parameters w(j) and b(j) for each user, we can use a cost function that measures the difference between the predicted rating and the actual rating given by the user. We will use the mean squared error as the cost function, which is defined as follows:

J(w(j), b(j)) = (1/2m(j)) * sum(i:r(i,j)=1) [(w(j).X(i)+b(j) - y(i,j))^2] + (lambda/2m(j)) * sum(k=1 to n) (w(j,k))^2

In this equation, m(j) is the number of movies user j has rated, n is the number of features (in our case, n=2), and lambda is the regularization parameter. The first term in the equation measures the difference between the predicted rating and the actual rating, summed over the movies that user j has rated. The second term in the equation is the regularization term, which penalizes large parameter values to avoid overfitting.

To learn the parameters for all users, we can use an optimization algorithm such as gradient descent to minimize the cost function for all users. Specifically, we can define the global cost function as follows:

J(w(1), b(1), ..., w(nu), b(nu)) = (1/nu) * sum(j=1 to nu) J(w(j), b(j))

In this equation, nu is the number of users. We can then use gradient descent or another optimization algorithm to minimize this cost function over all parameters w(j) and b(j).

Setup

Collaborative filtering is a popular technique in recommendation systems, used to make personalized recommendations based on past user behavior. In this article, we will explore how collaborative filtering can be used to learn features from user ratings using linear regression.

Assumptions

Suppose we have a dataset of movie ratings by users, where each movie is associated with two features, x1 and x2. We can use linear regression to predict the movie ratings based on these features. However, what if we don't have these features for a particular movie? In this case, we need to find appropriate values for x1 and x2 from the data.

Feature learning

Suppose we have learned the parameters w and b for the four users in our dataset. We can use these parameters to make reasonable estimates of the feature vectors x1 and x2 for the first two movies. We can then use these feature vectors to predict the ratings of other users and try to match them with the actual ratings.

To learn the features x1 and x2 for a specific movie, we can use a cost function that minimizes the squared difference between predicted and actual ratings. We can add a regularization term to prevent overfitting of the data. We can then sum this cost function over all movies to learn the features for all movies in the dataset.

Mathematical formulation

The cost function for learning the features x1 and x2 for a specific movie is:

J(x1,x2) = (1/2) Σj[r(i,j)=1] (w(j).x(i) - y(i,j))^2 + (λ/2) Σk(x(k,i))^2

where w(j) is the parameter vector for user j, x(i) is the feature vector for movie i, y(i,j) is the actual rating of user j for movie i, λ is the regularization parameter, r(i,j) is a binary variable indicating whether user j has rated movie i or not, and k represents the feature index (1 or 2) for movie i.

The first term of the cost function represents the squared difference between predicted and actual ratings, summed over all users who have rated the movie. The second term is the L2 regularization term, which penalizes large feature values to avoid overfitting.

To learn the features x1 and x2 for all movies in the dataset, we can sum the cost function over all movies:

J = Σi J(x1(i),x2(i))

where J(x1(i),x2(i)) is the cost function for movie i.

Optimization

To minimize the cost function, we can use gradient descent to iteratively update the parameters w(j), x1(i), and x2(i). The partial derivatives of the cost function with respect to the parameters are:

∂J/∂w(j) = Σi[r(i,j)=1] (w(j).x(i) - y(i,j))x(i) + λw(j)

∂J/∂x(k,i) = Σj[r(i,j)=1] (w(j).x(i) - y(i,j))w(j,k) + λx(k,i)

where w(j,k) is the k-th component of the parameter vector w(j).

We can update the parameters using the following update rules:

w(j) = w(j) - α∂J/∂w(j)

x(k,i) = x(k,i) - α∂J/∂x(k,i)

where α is the learning rate.

Collaborative filtering is a powerful technique for making personalized recommendations, especially when we don't have complete information about the items in our dataset. By learning features from user ratings using linear regression, we can make accurate predictions for new items based on past user behavior. The cost function we have derived in this article can be minimized using gradient descent to obtain the optimal values of parameters w and x for our model. Collaborative filtering has many applications in e-commerce, social media, and other areas where personalized recommendations can help improve user experience and engagement.

Binary labels

Recommendation systems or collaborative filtering algorithms are widely used in many applications to suggest articles or products to users based on their past behavior or preferences. In most cases, users provide ratings or reviews that reflect their level of satisfaction with the item. However, there are situations where binary labels are used instead of star ratings to indicate whether the user liked or did not like the item. In this article, we will explore how collaborative filtering algorithms can be generalized to work with binary labels and provide some implementation tips for better performance.

Binary labels in collaborative filtering

In collaborative filtering, binary labels are used to indicate whether the user liked or engaged with an item. The label "1" indicates that the user engaged with the item in some way, such as watching a movie until the end, clicking the "like" or "favorite" button, or spending at least 30 seconds on the item. The label "0" means that the user did not engage with the item, while the label "?" indicates that the user has not yet seen the item.

Generalizing collaborative filtering algorithms

To generalize the collaborative filtering algorithm for binary labels, we need to modify the cost function and the prediction model. Instead of the linear regression model used in the traditional algorithm, we use the logistic function to predict the probability that the user engages with the item. The logistic function maps any real input to a value between 0 and 1, which can be interpreted as the probability of the output being "1". The modified prediction model is given by:

Normalizing Means

When building a recommendation system, it is common to use numerical ratings, such as a scale from zero to five stars, to represent user preferences for different items. However, if you want your algorithm to work more efficiently and accurately predict ratings for new users who haven't yet rated many items, mean normalization can be an effective technique.

Mean normalization involves adjusting the ratings for each item so that they have a consistent mean value. To illustrate this, let's take a dataset with five movies and four users who have rated them, as well as a fifth user named Eve who hasn't rated any movies yet. We can represent this data in a matrix, where the rows correspond to the users and the columns correspond to the movies. The matrix will have some missing values because Eve hasn't rated any movies.

     Y = 
    [ 5 5 0 0  ? ]
    [ 5 ? 0 ?  2 ]
    [ ? 4 0 0  ? ]
    [ 0 0 5 5  0 ]
    [ ? ? ? ?  ? ]

In this matrix, missing values are represented by question marks. We want to predict ratings for user 5, Eve.

To perform mean normalization, we first calculate the average rating given to each film. Let's call this vector μ:

     μ = [ 2.5, 2.5, 2.0, 2.25, 1.25 ]

Then, we subtract the average rating for each movie from the original ratings given by each user. This new set of ratings becomes our input data for the recommendation algorithm. By subtracting the average rating for each movie, we ensure that our predictions are not biased towards highly rated movies. This gives us a new matrix Y_norm:

     Y_norm = 
    [ 2.5 2.5 -2.5 -2.5   ? ]
    [ 2.5  ?  -2.5  ?   -0.25 ]
    [  ?  2.0 -2.0 -2.0   ? ]
    [-2.25 -2.25 2.75 2.75 -2.25 ]
    [  ?   ?   ?   ?     ? ]

After adjusting the ratings using mean normalization, we can use the same collaborative filtering algorithm as before to predict ratings for new users like Eve. The algorithm learns parameters w(j), b(j), and x(i) to predict the rating for user j on movie i. Since we subtracted the mean rating for each movie, we need to add it back to ensure that our predictions are on the rating scale (0 to 5 stars, for example):

     w(5) = [ 0, 0, 0, 0, 0 ]
    b(5) = 0

To make a prediction for movie 1, we take the dot product of the weight vector w(5) and the feature vector x(1) for movie 1, and add the bias term b(5):

     w(5).x(1) + b(5) = 0 + 0 = 0

But because we subtracted the mean rating for movie 1 during mean normalization, we need to add it back to get the actual prediction:

     w(5).x(1) + b(5) + μ(1) = 0 + 0 + 2.5 = 2.5

We predict that Eve will rate movie 1 with 2.5 stars. We can make similar predictions for other movies. Note that because we initialized the parameters for user 5 to zero, we predict that Eve will rate all movies the same way, i.e., with the average rating of all users.

Mean normalization has several advantages. First, it makes the algorithm more accurate for new users who have not yet rated many items. Without mean normalization, the algorithm might predict that new users will rate all items very high or very low, depending on the overall rating distribution. By subtracting the mean rating for each movie, we can make more reasonable predictions for new users.

Second, mean normalization can also make the algorithm faster. By centering the ratings around zero, we reduce the number of parameters the algorithm needs to learn, which can speed up the training process.

In practice, there are two ways to perform mean normalization: by normalizing the rows or by normalizing the columns of the matrix. Normalizing rows may be more useful when dealing with new users who have not yet rated many items, while normalizing columns may be more useful when dealing with new items that have not yet been rated. However, for most recommendation systems, normalizing only the rows should work fine.

Ultimately, mean normalization is an effective technique for improving the accuracy and efficiency of a recommendation system, especially for new users who have not yet rated many items. By adjusting ratings to have a consistent average value, we can make more reasonable predictions and speed up the training process.

Finding Related Items

Collaborative filtering is an approach used in recommendation systems that involves learning feature vectors X for each item, such as movies, that are recommended to users. Feature vectors can help identify similar items and provide personalized recommendations to users.

To learn feature vectors X, we can use a matrix factorization approach that minimizes the sum of squared errors between the predicted rating and the actual rating. We define a matrix R, where R[i,j] represents the rating that user j gave to item i, and a matrix X, where X[i,:] represents the feature vector for item i. We also introduce a parameter matrix Theta, where Theta[j,:] represents the parameter vector for user j. We can then use the following optimization problem:

minimize: (1/2) * sum((R[i,j] - X[i,:] * Theta[j,:].T)^2) + (lambda/2) * sum(X[i,:]^2) + (lambda/2) * sum(Theta[j,:]^2)

subject to: Theta[j,:] represents the parameter vector for user j lambda represents a regularization parameter

The optimization problem aims to learn the feature vectors X and parameter vectors Theta by minimizing the sum of squared errors between the predicted rating and the actual rating. We add regularization terms to prevent overfitting.

In the end, mean normalization is an effective technique for improving the accuracy and efficiency of a recommendation system, especially for new users who have not yet rated many items. By adjusting the ratings to have a consistent average value, we can make more reasonable predictions and speed up the training process.

Finding Related Items

Collaborative filtering is an approach used in recommendation systems that involves learning feature vectors X for each item, such as movies, that are recommended to users. The feature vectors can help identify similar items and provide personalized recommendations to users.

To learn the feature vectors X, we can use a matrix factorization approach that minimizes the sum of squared errors between the predicted rating and the actual rating. We can define a matrix R, where R[i,j] represents the rating that user j gave to item i, and a matrix X, where X[i,:] represents the feature vector for item i. We also introduce a parameter matrix Theta, where Theta[j,:] represents the parameter vector for user j. We can then use the following optimization problem:

minimize: (1/2) * sum((R[i,j] - X[i,:] * Theta[j,:].T)^2) + (lambda/2) * sum(X[i,:]^2) + (lambda/2) * sum(Theta[j,:]^2)

subject to: Theta[j,:] represents the parameter vector for user j lambda represents a regularization parameter

The optimization problem aims to learn the feature vectors X and the parameter vectors Theta by minimizing the sum of squared errors between the predicted rating and the actual rating. We add regularization terms to avoid overfitting.

To find similar items, we can calculate the squared distance between the feature vectors of two items i and k using the following equation:

distance = sum((X[i,:] - X[k,:])^2)

If we want to find the top k most similar items to item i, we can calculate the distance between i and all other items, sort the distances in ascending order, and select the top k items.

For example, if we have a matrix R that represents the ratings given by users to movies, and a matrix X that represents the feature vectors of the movies, we can use collaborative filtering to identify similar movies. Suppose we want to find the five most similar movies to a given movie i. We can calculate the distance between movie i and all other movies using the above equation, sort the distances in ascending order, and select the top five movies.

Collaborative filtering has some limitations, such as the cold-start problem, where new items or new users have limited data to provide accurate recommendations. Additionally, collaborative filtering does not take into account additional information, such as the genre of a movie or the demographic information of a user. However, content-based filtering algorithms can address these limitations by incorporating additional information.

Conclusion

In conclusion, generalizing collaborative filtering algorithms for binary labels can greatly expand the set of applications in which these algorithms can be used. By modifying the cost function and prediction model, we can predict the probability that a user will engage with an item and recommend items to users based on these predictions. The use of implementation tricks such as sparse matrices, regularization, mini-batch gradient descent, and early stopping can also improve algorithm performance. As the use of binary labels becomes increasingly common in many online applications, it is important to understand how to adapt collaborative filtering algorithms to this context. We hope that this article provides a useful introduction to this topic and encourages further exploration and development of these algorithms.