The Boltzmann Machine

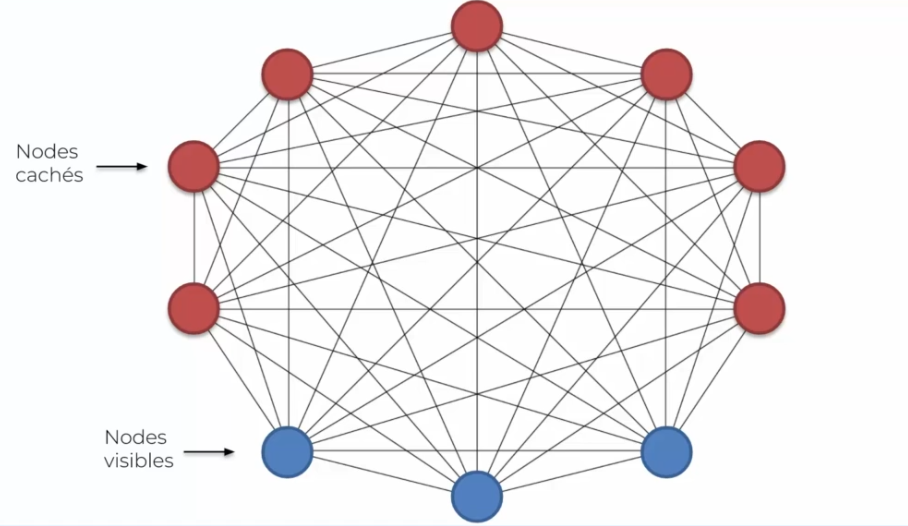
One of the characteristics of these machines, and what makes them unique, is that a Boltzmann machine does not have a direction. What we noticed in the figure above is that all neurons are connected together. Input neurons are connected to each other, just as hidden neurons are connected to each other. It is also noted that each input neuron is also connected to each hidden neuron. This is what characterizes the Boltzmann machine!

But where to start to understand well?

Let's start with the visible nodes (in blue) that surprisingly connect to each other, while normally in the neural networks we have seen previously, they were only connected to hidden neurons. In addition, these input nodes are input data that represent data, so what is the interest of connecting this data to each other? Well, Boltzmann machines are different, they do not limit themselves to input data, but they generate their own. Another important point is that we make a distinction between input and hidden neurons, whereas the Boltzmann machine does not. In other words, a Boltzmann machine is capable of creating states randomly, and observing the impact of these states on the system to learn more. This observation is based on our input data, indeed it will use this data to adjust its weights. These data are considered as the data of a stable state. In the long term, we therefore obtain a copy of this machine, which has tested several states and understands normality. Let us well remember this word normality, based on our inputs, which will allow the Boltzmann machine to detect an abnormality (unsupervised model). This is its only goal, because the machine only has data when everything is going well and when there will be divergences, the model will quickly detect it.

So it is normal not to have an output, as we do not need a prediction here, but an alert in case of abnormality.

The energy model

We can mathematically represent the Boltzmann machine as follows:

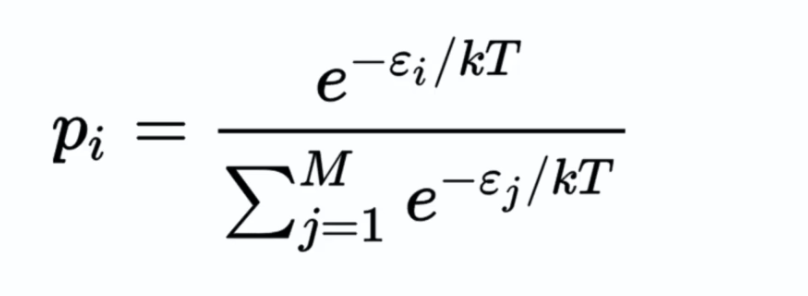
The energy model refers to a probability on a state with the lowest energy: a drop of ink in water does not spread in the form of a star, for example, in this case the energy is high because this state is unlikely and will require more energy to be realized to simulate the non-existent state. This process allows us to evaluate the energy for each state or simply the weights on each synapse, in order to find the state with the lowest energy.

We therefore have a series of states, for example the diffusion of gas in the air:

• Low energy: the state is that the gas diffuses throughout the room, it is a current state
• High energy: the state is that the gas stagnates in the corner of a room, it is an almost improbable state

The restricted Boltzmann Machine

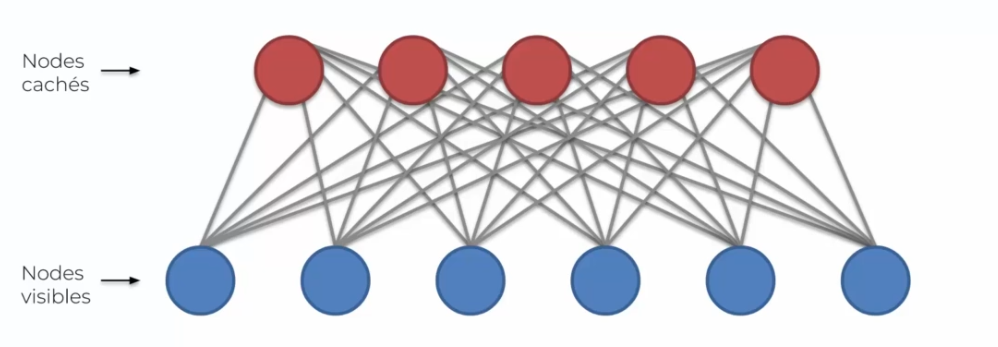
Unlike the Boltzmann machine previously seen, all neurons are no longer connected to each other. But we still do not have a direction, which is one of the characteristics of this model. Here we want the system to adapt to our data, rather than simulate data as explained earlier.

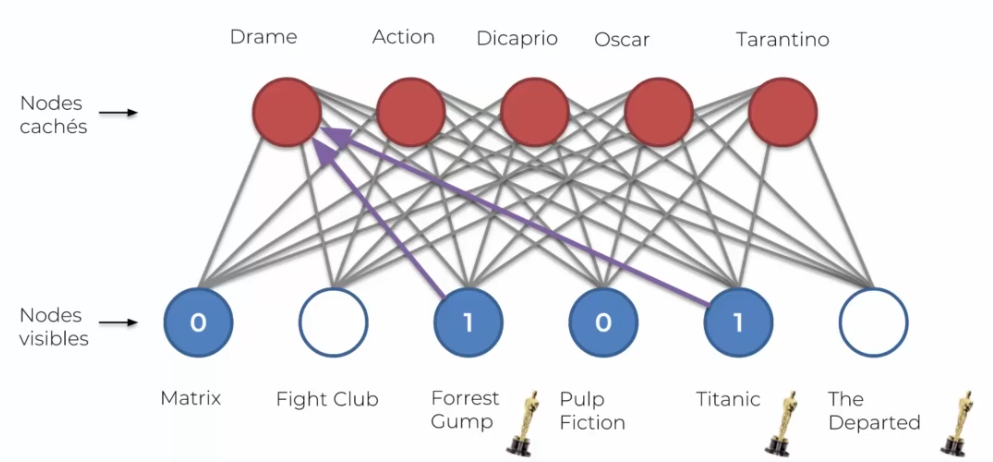
As input, we could have movies:

• Inception
• Batman
• Star wars
• The Lord of the Rings

As output, we could have genres:

• Science fiction
• Heroics
• Fantasy

See actors;

• Christian Bale

See even directors:

• Nolan
• George Lucas

The neurons do not know what they represent, it is us who put names on them. Learning begins by giving one line at a time:

	Movie 1	Movie 2	Movie 3	Movie 4	Movie 5	Movie 6
User 1	1	0		1	1	1
User 1	0	1	0	0	1	0
User 3		1	1	0	0
User 4	1	0	1	1	0	1
User 5	0		1	1		1
User 6	0	0	0	0	1
User 7	1	0	1	1	0	1
User 8	0	1	1		0	1
User 9		0	1	1	1	1
User 10	1		0	0		0

The user's opinion is characterized by 0 or 1 if one liked it, and nothing if one has not seen it. Thus, we can have preferences that go together: I liked movie 3 and 4 so maybe I would like movie 6. The Boltzmann machine will identify this relationship and create a node for this preference, for example genre 1 (always a human nomination and not a machine). The execution can be represented through this diagram:

Divergence contrastive

This is the algorithm that allows our machine to learn. In most networks, we had backpropagation that we do not have with Boltzmann. So how does it work?

• We have hidden networks
• We have input networks
• At the start, each neuron starts with random weights

Let's start:

1. The first step is to calculate the hidden nodes
2. Once calculated, we will reuse the same weights to calculate the input nodes, however, the nodes that will be recalculated will no longer be the same as at the beginning! Indeed, since all neurons allow the recalculation of the cost, this leads to a divergence on the node

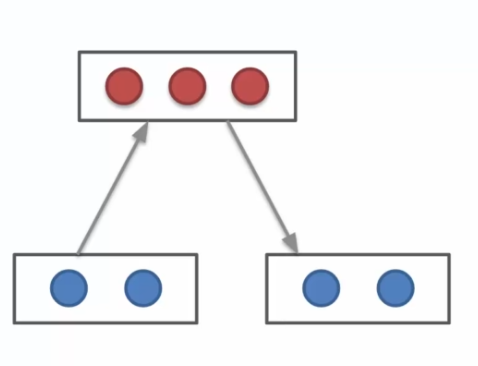
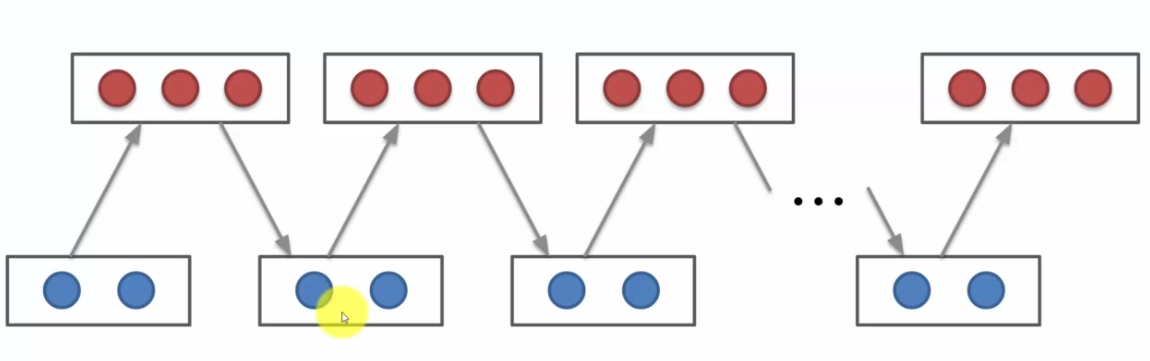
3. Repeat steps 1 and 2 until the end, we then say that we are sampling. We then have convergence of the algorithm, which will allow the model to create exactly our input data to simulate the different states of the system.

Now let's see how this weight update takes place:

1. We will create our gradient as an input
2. This gradient will equal our energy at the starting point (our green point) minus our energy at the end
3. Gradually, the energy will decrease until it reaches the lowest energy state

Here, our minimum energy is the trough of the curve, our starting weight represents the green weight, and the red weight is the evolution of our weight during the first calculation. Basically, we want our gradient to be equal to 0, which means that we have reached the minimum.

If we take the explanation from the beginning: our weights are random until sampling, which gives us the direction in which we update our weights:

This direction will allow us to adjust our energy curve, which will allow us to be at the minimum energy value after several updates:

Deep Belief Network

This network is a stacking of Boltzmann machines, where we add several hidden curves. But we have another difference, we have the notion of direction going from top to bottom.

To train this type of network, there are two algorithms:

• Layer-by-layer training: We train layer by layer, without any notion of direction. It's only at prediction level that we add the arrows. (Most used)
• Bottom-up and then top-down training.