Introduction

Anomaly detection is a machine learning technique used to identify unusual or abnormal events in a set of unlabeled normal event data. The algorithm learns to detect anomalies by analyzing a set of features in the data and raising a red flag if the new event appears different from previous ones. For example, anomaly detection can be used to detect defects in airplane engines after manufacturing to avoid potential failures that can have negative consequences.

To illustrate how anomaly detection works, consider a dataset of airplane engines with two features: heat generated (x1) and vibration intensity (x2). When a new airplane engine is produced, the algorithm calculates the values of x1 and x2 for the new engine and plots them graphically alongside the previous engines. If the new engine falls within the range of values seen before, the algorithm considers it normal and does not raise a flag. However, if the new engine has a significantly different heat and vibration signature, the algorithm identifies it as an anomaly and recommends further inspection.

The most common method for performing anomaly detection is density estimation, where the algorithm constructs a model of the probability distribution of the features in the dataset. The algorithm learns to recognize regions of data with higher or lower probabilities and uses this information to identify anomalies. When a new event is encountered, the algorithm calculates its probability based on the model and compares it to a small threshold value (epsilon). If the probability is lower than epsilon, the algorithm raises a flag for an anomaly.

Anomaly detection is used in various applications, such as fraud detection, manufacturing, and computer monitoring. In fraud detection, the algorithm can be used to identify unusual patterns in user activity, such as unusual login frequency or transaction volume, which may indicate fraudulent behavior. In manufacturing, the algorithm can be used to identify abnormal parts, such as faulty circuit boards or defective smartphones, to avoid shipping faulty products to customers. In computer monitoring, the algorithm can identify abnormal behaviors in a machine, such as high memory usage or CPU load, which may indicate a failure or security breach.

Gaussian

Anomaly detection is a commonly used technique in data analysis to identify unusual or abnormal instances in a dataset. The first step in this process is to model the distribution of the data, and the Gaussian distribution (also known as the normal distribution) is a popular choice for this purpose. In fact, the bell-shaped curve you may have heard of refers to the Gaussian distribution

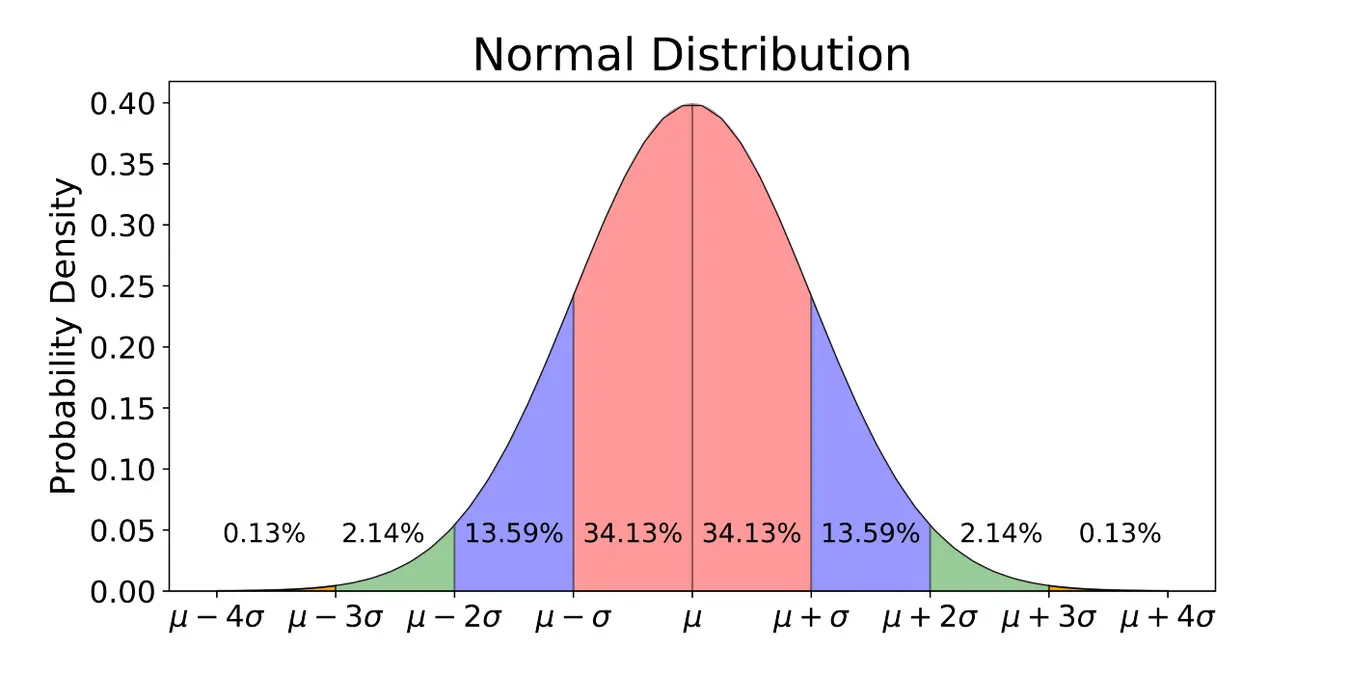
When modeling data using the Gaussian distribution, we assume that the data follows a probability distribution described by a bell-shaped curve. The center of this curve, called the mean parameter µ, represents the most likely value of the data. The standard deviation of the curve, indicated by Sigma, describes the spread of the data around the mean. The curve is mathematically represented by the probability density function (PDF):

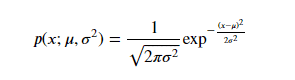
To apply anomaly detection using the Gaussian distribution, we need to estimate the values of µ and Sigma that best describe the data. We do this using the maximum likelihood estimation method, where µ is estimated as the mean of the training examples, and Sigma is estimated as the mean of the squared difference between the training examples and the estimated value of µ:

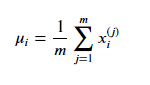
Once we have estimated these parameters, we can use the PDF to calculate the probability that a new instance is a normal or abnormal data point.

In practice, datasets typically have multiple features, and we need to extend the Gaussian distribution to handle this case. To do this, we assume that each feature follows a Gaussian distribution with its own mean and standard deviation. We can then combine these distributions to form a multivariate Gaussian distribution that models the joint probability of all the features. The PDF for a multivariate Gaussian distribution is given by:

p(x) = (1 / ((2 * pi)^(n/2) * det(Sigma)^0.5)) * exp(-0.5 * (x - µ)' * inv(Sigma) * (x - µ)),

where n is the number of features, µ is a vector of means, Sigma is a covariance matrix, and inv(Sigma) is the inverse of Sigma:

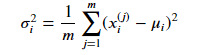
In summary, the Gaussian distribution is a useful tool for modeling the distribution of data in anomaly detection. By estimating the mean and standard deviation of the distribution, we can identify anomalous instances in a dataset. The multivariate Gaussian distribution extends this concept to datasets with multiple features, allowing us to model the joint probability of all features.

Algorithm

To build an anomaly detection algorithm, the first step is to select the features xi that could be indicative of anomalous examples. We then estimate the parameters µ1 to µn and Sigma²1 to Sigma²n for the n features in our dataset using the maximum likelihood estimation method.

The model of p(x), the probability of any given feature vector, is then calculated as the product of the probability of each individual feature using the Gaussian distribution. If we have n features, then the product of the probability of each feature can be written as the product from j = 1 to n of p(xj) with the parameters µj and Sigma²j.

Once we have estimated these parameters, we can calculate p(x) for a new example x and compare it to a predefined threshold value epsilon. If p(x) is lower than epsilon, we flag the example as an anomaly.

The intuition behind this algorithm is that it tends to flag an example as anomalous if one or more features are very large or very small compared to what it has seen in the training set. This is done by fitting a Gaussian distribution for each feature xj and checking if the probability of the individual feature is low.

To choose the parameter epsilon, we usually use a validation set and select the value that gives us the best trade-off between false positives and false negatives.

Anomaly detection using the Gaussian distribution is a useful tool for identifying anomalous instances in a dataset. By estimating the mean and standard deviation of the distribution for each individual feature, we can flag examples that are statistically different from the training set.

Developing and evaluating a system

In the development of a system, the ability to evaluate it as it progresses can greatly facilitate decision-making and system improvement. This is particularly true in the development of learning algorithms. For example, when developing a learning algorithm, it may be necessary to make decisions about feature selection or the choice of parameter values such as epsilon. If there is a way to evaluate the algorithm during development, such as through real-number evaluation, the decision-making process becomes much simpler. Real-number evaluation involves the ability to quickly change the algorithm and calculate a number that indicates whether the change has made the algorithm better or worse.

Anomaly detection is an example of an application where real-number evaluation is particularly useful. Although we have mainly talked about unlabeled data, it is possible to incorporate labeled data into the anomaly detection process. By using a small number of labeled anomalous examples, a cross-validation set can be created that can be used to evaluate the algorithm. The cross-validation set includes both normal and anomalous examples, and the algorithm is trained on a separate set of normal examples.

For example, consider anomaly detection in airplane engines. Suppose we have collected data from 10,000 good engines and 20 anomalous engines. We can divide this data into a training set, a cross-validation set, and a test set. The training set includes 6,000 good engines, and the cross-validation set includes 2,000 good engines and 10 anomalous engines. The test set includes 2,000 good engines and 10 anomalous engines.

The algorithm is trained on the training set by fitting Gaussian distributions to the normal examples. The cross-validation set is then used to tune the epsilon parameter and evaluate the algorithm's ability to correctly identify anomalous engines. The algorithm is then evaluated on the test set to determine its performance.

When evaluating the algorithm, a real-number evaluation is performed by calculating p(x), the probability that a given example x is normal, and comparing it to a chosen value of epsilon. If p(x) is less than epsilon, the example is identified as anomalous. Evaluation is typically performed using metrics such as precision, recall, F1 score, or classification accuracy, especially when the distribution of positive and negative examples is heavily imbalanced.

Although labeled data can be used in anomaly detection, it is still primarily an unsupervised learning algorithm. However, the integration of labeled examples into the evaluation process can greatly facilitate the development of the algorithm. Despite this, it may be tempting to use a supervised learning algorithm when labeled examples are available. However, unsupervised learning algorithms are still preferred because they do not require a labeled dataset for training, which can be difficult to obtain for some applications.

Some features used

In machine learning, feature selection is one of the essential aspects of building effective models. In particular, selecting the right set of features is crucial for anomaly detection, where the model learns only from unlabeled data. In this blog post, we will explore some practical tricks for feature selection in anomaly detection.

The importance of Gaussian features

One way to ensure that your features are suitable for anomaly detection is to make sure they are approximately Gaussian. Gaussian features have the advantage of being symmetric and unimodal, making them easier to model using probability distributions like the normal distribution. In contrast, non-Gaussian features can be more challenging to model and may require complex transformations to be used appropriately in a model.

Let's take the example of a feature X. To check if it is Gaussian, we can plot a histogram of X using the Python command plt.hist(X). If the histogram looks like a symmetrical bell curve, the feature is probably Gaussian. However, if the histogram is not symmetrical, the feature is non-Gaussian and requires a transformation.

Transforming non-Gaussian features

One of the most common ways to transform non-Gaussian features is to take the logarithm of the feature. This transformation is useful for features that have a long tail towards higher values, making them non-Gaussian. By applying the logarithm, we can compress the tail and make the feature more symmetrical.

Another way to transform non-Gaussian features is to raise them to a fractional power. For example, we can take the square root of a feature X using the Python command np.sqrt(X) to create a new feature. This transformation is useful for features that have a long tail towards lower values.

Let's take the example of a non-Gaussian feature X1 that has a long tail towards higher values. To transform X1, we can apply the logarithmic transformation using the Python command np.log(X1). We can then plot the histogram of the transformed feature using plt.hist(np.log(X1)). If the histogram looks more Gaussian, we can use the transformed feature in our model instead of the original feature.

Similarly, let's take another example of a non-Gaussian feature, X2, that has a long tail towards lower values. To transform X2, we can take its square root using the Python command np.sqrt(X2). We can then plot the histogram of the transformed feature using plt.hist(np.sqrt(X2)). If the histogram looks more Gaussian, we can use the transformed feature in our model instead of the original feature.

Exploration of different transformations

In practice, it may be necessary to try several different transformations to find the one that best suits our data. For example, we can try different fractional powers for a feature or different base values for logarithmic transformations.

To explore different transformations, we can plot the histogram of each transformed feature using plt.hist(transformed feature), where transformed feature is the result of applying a specific transformation to the original feature. By visualizing the histograms, we can select the transformation that produces the most Gaussian feature.

Conducting an error analysis

Even with Gaussian features, anomaly detection models do not always detect anomalies accurately. In such cases, it is helpful to conduct an error analysis to identify the types of anomalies that the model is failing to detect. Depending on the results of the error analysis, we can generate new features to distinguish between normal and abnormal examples.

For example, suppose we are building an anomaly detection system to monitor computers in a data center. We might start with features such as memory usage, disk accesses per second, processor load, and network traffic volume. If the model fails to detect certain anomalies, we can create new features by combining the old ones or introducing new ones. For example, we can calculate the ratio of processor load to network traffic volume, or the square of processor load divided by network traffic volume. By doing so, we can create a new feature that is more sensitive to specific types of anomalies.

Once we have created new features, we need to update our anomaly detection model by incorporating the new features. We can then evaluate the performance of the updated model by comparing its predictions with the actual anomalies in our dataset. This will help us determine whether the new features have improved the performance of our model.

In conclusion, careful feature selection is crucial for building an effective anomaly detection system. It is particularly important to ensure that features are approximately Gaussian, as this can significantly improve the performance of the model. If the model fails to detect anomalies accurately, we can perform an error analysis to identify the types of anomalies that are not being detected and create new features to fill these gaps. By iteratively refining the features and the model, we can build a robust and accurate anomaly detection system.