Switch-case blog - Tensorflow

Introduction

TensorFlow est une plateforme open-source populaire pour le développement de modèles d'apprentissage automatique, et elle est rapidement devenue un outil incontournable pour les développeurs et les scientifiques des données. Une des caractéristiques clés de TensorFlow est la possibilité de créer des modèles séquentiels pouvant être utilisés pour diverses tâches, telles que la classification d'images ou le traitement du langage naturel.

Dans cet article, nous explorerons certaines des fonctionnalités principales de TensorFlow et expliquerons comment elles fonctionnent. Plus précisément, nous aborderons le modèle séquentiel, les couches denses, la méthode de compilation, la méthode d'ajustement et la méthode de prédiction. Plongeons !

Modèle séquentiel

Le modèle séquentiel est le modèle le plus couramment utilisé dans TensorFlow. Il vous permet de créer une pile linéaire de couches, où chaque couche a une seule entrée et sortie. Pour créer un modèle séquentiel, vous instanciez simplement la classe Sequential :

 from tensorflow.keras.models import Sequential
model = Sequential()

Une fois que vous avez créé votre modèle séquentiel, vous pouvez lui ajouter des couches en utilisant la méthode add.

Couche dense

Les couches denses sont le type de couche le plus couramment utilisé dans TensorFlow. Ce sont des couches entièrement connectées, ce qui signifie que chaque neurone de la couche est connecté à chaque neurone de la couche précédente. Vous pouvez créer une couche dense en utilisant la classe Dense :

 from tensorflow.keras.layers import Dense
layer = Dense(units=128, activation='relu', input_shape=(784,))

Ici, nous créons une couche dense avec 128 unités, une fonction d'activation ReLU et une forme d'entrée de 784 (qui correspond à une image 28x28 aplatie).

Méthode de compilation

Une fois que vous avez créé votre modèle et ajouté des couches, vous devez le compiler avant de pouvoir l'entraîner. La méthode de compilation vous permet de spécifier l'optimiseur, la fonction de perte et les métriques que vous souhaitez utiliser. Voici un exemple de compilation d'un modèle :

 model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

Dans cet exemple, nous utilisons l'optimiseur Adam, la fonction de perte d'entropie croisée catégorique, et la précision comme notre métrique.

Méthode Fit

Après avoir compilé votre modèle, vous pouvez le former en utilisant la méthode fit. La méthode fit prend en entrée vos données d'entraînement, ainsi que le nombre d'époques (ou itérations) que vous souhaitez exécuter. Voici un exemple de montage d'un modèle :

 historique = model.fit(X_train, y_train, epochs=10, validation_data=(X_val, y_val))

Dans cet exemple, nous adaptons le modèle à nos données d'entraînement (X_train, y_train) pour 10 époques, et nous utilisons nos données de validation (X_val, y_val) pour évaluer le modèle après chaque époque.

Méthode Predict

Enfin, après avoir formé votre modèle, vous pouvez utiliser la méthode predict pour faire des prédictions sur de nouvelles données. La méthode predict prend en entrée vos données de test et renvoie des prédictions pour chaque entrée. Voici un exemple de l'utilisation de la méthode predict :

 y_pred = model.predict(X_test)

Dans cet exemple, nous utilisons notre modèle formé pour faire des prédictions sur nos données de test (X_test), et nous stockons les prédictions dans y_pred.

MNIST

MNIST est un ensemble de données bien connu dans le domaine de l'apprentissage machine, particulièrement dans le domaine de la classification d'images. Il représente l'Institut National des Standards et de la Technologie Modifiés, et il se compose d'un ensemble de 70 000 images en niveaux de gris de chiffres manuscrits (0-9), chaque image ayant une résolution de 28x28 pixels.

L'ensemble de données est couramment utilisé comme référence pour tester la précision et l'efficacité de divers algorithmes d'apprentissage machine. Les images sont prétraitées et normalisées pour avoir des valeurs entre 0 et 1, ce qui facilite l'apprentissage des modèles d'apprentissage machine à partir des données.

MNIST est souvent utilisé comme point de départ pour les débutants pour apprendre la classification d'images et l'apprentissage machine en général. Il est également utilisé comme ensemble de données de référence pour comparer les performances de nouveaux modèles et algorithmes, car de nombreux modèles de pointe ont été testés sur cet ensemble de données et ont atteint des niveaux élevés de précision.

Importer l'ensemble de données MNIST

 # Charger les données depuis keras
fashion_mnist = tensorflow.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()

Commençons

La première couche est une couche de mise à plat qui prend des images de 28 par 28 pixels, et les convertit en un tableau linéaire. La deuxième ou couche intermédiaire est une couche cachée avec 128 neurones ou variables, que le réseau utilise pour créer une fonction complexe pour classifier les images. Enfin, la dernière couche a 10 neurones, un pour chaque classe de vêtements dans l'ensemble de données, et produit une distribution de probabilité sur ces classes.

La clé pour comprendre ce réseau est de penser à la couche du milieu comme un ensemble de variables (x1, x2, x3, etc.) qui peuvent être combinées dans une somme pondérée pour produire une valeur de sortie. Ceci est similaire à l'équation y = w1x1 + w2x2 + ... + w128x128, où les poids (w1, w2, ..., w128) sont appris par le réseau pendant l'entraînement. Lorsqu'une image d'entrée est donnée, le réseau calcule les valeurs de ces variables et les utilise pour produire une distribution de probabilité sur les classes de vêtements dans l'ensemble de données.

 de keras.models importer Sequential
de keras.layers importer Flatten, Dense

# créer un modèle séquentiel
model = Sequential()

# ajouter une couche de mise à plat pour convertir les images d'entrée en un tableau linéaire
model.add(Flatten(input_shape=(28, 28)))

# ajouter une couche cachée avec 128 neurones et une fonction d'activation ReLU
model.add(Dense(128, activation='relu'))

# ajouter une couche finale avec 10 neurones et une fonction d'activation softmax
model.add(Dense(10, activation='softmax'))

# compiler le modèle avec une perte d'entropie croisée catégorique et un optimiseur Adam
model.compiler(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

Dans cet exemple, nous créons un modèle séquentiel et ajoutons une couche d'aplatissement avec une forme d'entrée de 28 par 28. Nous ajoutons ensuite une couche cachée avec 128 neurones et une fonction d'activation ReLU, et une couche finale avec 10 neurones et une fonction d'activation softmax. Enfin, nous compilons le modèle avec une perte d'entropie croisée catégorielle et un optimiseur Adam. Ce modèle peut être formé et utilisé pour classer les images de vêtements en l'une des 10 classes.

Pour mieux comprendre les valeurs dans l'ensemble de données MNIST, nous pouvons imprimer une image d'entraînement et son étiquette correspondante. Nous pouvons utiliser la bibliothèque NumPy pour manipuler les données et Matplotlib pour visualiser l'image. En expérimentant avec différents indices dans le tableau, nous pouvons voir différents exemples de chiffres écrits à la main.

Par exemple, nous pouvons imprimer l'image et l'étiquette à l'indice 0 ou 42 pour comparer deux images différentes de bottes. Il est également important de noter que les valeurs de pixel des images sont comprises entre 0 et 255, ce qui n'est pas optimal pour former un réseau neuronal. Par conséquent, nous normalisons les valeurs de pixel en les divisant par 255,0, afin qu'elles tombent entre 0 et 1, ce qui aidera le réseau neuronal à mieux apprendre.

 import numpy as np
import matplotlib.pyplot as plt

# Imprimez une image d'entraînement et son étiquette correspondante
index = 0
np.set_printoptions(linewidth=320)
print(f'ÉTIQUETTE : {training_labels[index]}')
print(f'\nTABLEAU DE PIXELS DE L'IMAGE:\n {training_images[index]}')
plt.imshow(training_images[index])

# Normalisez les valeurs de pixel des images d'entraînement et de test
training_images = training_images / 255.0
test_images = test_images / 255.0

Dans cet exemple, nous définissons d'abord l'indice à 0 pour imprimer la première image d'entraînement et son étiquette correspondante. Nous utilisons la méthode set_printoptions de NumPy pour définir le nombre de caractères par ligne lors de l'impression, puis imprimons l'étiquette et le tableau de pixels de l'image.

Nous utilisons ensuite la méthode imshow de Matplotlib pour visualiser l'image. Enfin, nous normalisons les valeurs de pixel des images d'entraînement et de test en les divisant par 255,0, ce qui échelonne les valeurs entre 0 et 1.

C'est le résultat :

 IMAGE PIXEL ARRAY:
 [[  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0  82 187  26   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   1   0   0   1   0   0 179 240 237 255 240 139  83  64  43  60  54   0   1]
 [  0   0   0   0   0   0   0   0   0   1   0   0   1   0  58 239 222 234 238 246 252 254 255 248 255 187   0   0]
 [  0   0   0   0   0   0   0   0   0   0   2   3   0   0 194 239 226 237 235 232 230 234 234 233 249 171   0   0]
 [  0   0   0   0   0   0   0   0   0   1   1   0   0  10 255 226 242 239 238 239 240 239 242 238 248 192   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0 172 245 229 240 241 240 241 243 243 241 227 250 209   0   0]
 [  0   0   0   0   0   0   0   0   0   6   5   0  62 255 230 236 239 241 242 241 242 242 238 238 242 253   0   0]
 [  0   0   0   0   0   0   0   0   0   3   0   0 255 235 228 244 241 241 244 243 243 244 243 239 235 255  22   0]
 [  0   0   0   0   0   0   0   0   0   0   0 246 228 220 245 243 237 241 242 242 242 243 239 237 235 253 106   0]
 [  0   0   3   4   4   2   1   0   0  18 243 228 231 241 243 237 238 242 241 240 240 240 235 237 236 246 234   0]
 [  1   0   0   0   0   0   0   0  22 255 238 227 238 239 237 241 241 237 236 238 239 239 239 239 239 237 255   0]
 [  0   0   0   0   0  25  83 168 255 225 225 235 228 230 227 225 227 231 232 237 240 236 238 239 239 235 251  62]
 [  0 165 225 220 224 255 255 233 229 223 227 228 231 232 235 237 233 230 228 230 233 232 235 233 234 235 255  58]
 [ 52 251 221 226 227 225 225 225 226 226 225 227 231 229 232 239 245 250 251 252 254 254 252 254 252 235 255   0]
 [ 31 208 230 233 233 237 236 236 241 235 241 247 251 254 242 236 233 227 219 202 193 189 186 181 171 165 190  42]
 [ 77 199 172 188 199 202 218 219 220 229 234 222 213 209 207 210 203 184 152 171 165 162 162 167 168 157 192  78]
 [  0  45 101 140 159 174 182 186 185 188 195 197 188 175 133  70  19   0   0 209 231 218 222 224 227 217 229  93]
 [  0   0   0   0   0   0   2  24  37  45  32  18  11   0   0   0   0   0   0  72  51  53  37  34  29  31   5   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]
 [  0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0]]

Process finished with exit code 0

Le jeu de données MNIST est divisé en deux ensembles : l'entraînement et le test. L'ensemble d'entraînement est utilisé pour entraîner le modèle, tandis que l'ensemble de test est utilisé pour évaluer la précision du modèle sur des données qu'il n'a jamais vues auparavant. Cette approche aide à prévenir le surapprentissage, où le modèle fonctionne bien sur les données d'entraînement mais mal sur les nouvelles données invisibles.

Concevoir le modèle de réseau neuronal peut sembler décourageant, mais nous pouvons le décomposer en concepts plus petits pour le rendre plus gérable. Nous pouvons utiliser diverses couches, telles que les couches Dense, pour créer un modèle qui peut classifier les chiffres écrits à la main dans l'ensemble de données. Avec un peu de pratique, nous pouvons créer des modèles complexes qui atteignent une haute précision sur l'ensemble de données MNIST et des tâches de classification d'images similaires.

Activation

L'unité de rectification linéaire (ReLU) est une fonction d'activation utilisée dans les réseaux de neurones qui passe efficacement les valeurs supérieures à 0 à la couche suivante du réseau. La fonction retourne x si x est supérieur à 0 et 0 si x est inférieur ou égal à 0. Cela aide à introduire une non-linéarité dans le modèle, le rendant plus flexible et mieux capable d'apprendre les motifs complexes dans les données.

La fonction Softmax est utilisée dans la couche de sortie d'un réseau neuronal pour convertir un ensemble de valeurs en une distribution de probabilité. Elle prend une liste de valeurs et les met à l'échelle de sorte que la somme de tous les éléments soit égale à 1. Les valeurs mises à l'échelle peuvent ensuite être interprétées comme la probabilité de chaque classe. Par exemple, dans un modèle de classification avec 10 unités dans la couche dense de sortie, la valeur la plus élevée à l'index = 4 indique que le modèle est le plus confiant que l'image de vêtement d'entrée est un manteau. Si la valeur la plus élevée est à l'index = 5, alors le modèle est le plus confiant que l'image d'entrée est une sandale, et ainsi de suite.

Callback

Une question courante qui se pose lors de l'expérimentation avec différents nombres d'époques est de savoir comment arrêter l'entraînement lorsqu'un certain point est atteint, sans coder en dur un nombre spécifique d'époques. Heureusement, la boucle d'entraînement dans TensorFlow prend en charge les callbacks, qui peuvent être utilisés pour exécuter une fonction de code après chaque époque et vérifier les métriques pour déterminer si l'on continue ou annule l'entraînement.

Pour mettre en œuvre cela, nous créons d'abord une classe séparée en Python qui contient la fonction on_epoch_end, qui est appelée par le callback après chaque époque et reçoit un objet logs contenant des informations sur l'état actuel de l'entraînement. Dans le code d'exemple, le callback vérifie si la perte est inférieure à 0,4 et annule l'entraînement si c'est le cas.

Ensuite, nous instancions la classe de callback et la passons au paramètre callbacks dans la fonction model.fit pour l'utiliser pendant l'entraînement. Avec cette configuration, nous pouvons arrêter dynamiquement l'entraînement lorsqu'un certain critère est atteint, sans avoir besoin de spécifier manuellement le nombre d'époques.

Voici un exemple de code qui montre comment utiliser un callback pour arrêter l'entraînement :

 import tensorflow as tf

class StopTrainingCallback(tf.keras.callbacks.Callback):
    def on_epoch_end(self, epoch, logs={}):
        if(logs.get('loss') < 0.4):
            print("\nAtteint la perte souhaitée, annulation de l'entraînement !")
            self.model.stop_training = True

# Instancier la classe de callback
callbacks = StopTrainingCallback()

# Entraîner le modèle et utiliser le callback pendant l'entraînement
model.fit(x_train, y_train, epochs=10, callbacks=[callbacks])

Dans cet exemple, nous créons une classe appelée StopTrainingCallback qui implémente la fonction on_epoch_end. Cette fonction vérifie si la perte actuelle est inférieure à 0,4 et définit l'attribut stop_training à True si c'est le cas.

Nous instancions ensuite la classe de callback et la passons au paramètre callbacks dans la fonction model.fit. Avec cette configuration, le callback est utilisé pendant l'entraînement et annulera l'entraînement lorsque la perte souhaitée sera atteinte.

définissons un exemple réel :

 # Remember to inherit from the correct class
class myCallback(tf.keras.callbacks.Callback):
        # Define the correct function signature for on_epoch_end
        def on_epoch_end(self, epoch, logs={}):
            if logs.get('accuracy') is not None and logs.get('accuracy') > 0.99:                 
                print("\nReached 99% accuracy so cancelling training!")
                
                # Stop training once the above condition is met
                self.model.stop_training = True

Maintenant, vous devriez pouvoir lier ceci à notre code pour interpréter le callback pendant un entraînement :

 #Construire le modèle de classification
#La première couche est un calque de mise à plat pour les images
#Le dernier neurone a 10 neurones car nous avons 10 catégories
def build_model():# Instancier la classe
    callbacks = myCallback()
    model = keras.Sequential([
        keras.layers.Flatten(input_shape=(28,28)),
        keras.layers.Dense(128, activation=tensorflow.nn.relu),
        keras.layers.Dense(10, activation=tensorflow.nn.softmax),
    ])

    model.compile(optimizer=tensorflow.optimizers.Adam(),
                  loss='crossentropie_catégorique_sparse',
                  metrics=['précision'])

    model.fit(train_images, train_labels, epochs=5, callbacks=[callbacks])
    return model

Cela devrait être le résultat de notre modèle :

 Epoch 1/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.2568 - accuracy: 0.9260
Epoch 2/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.1136 - accuracy: 0.9672
Epoch 3/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0795 - accuracy: 0.9755
Epoch 4/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0575 - accuracy: 0.9828
Epoch 5/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0456 - accuracy: 0.9860
Epoch 6/10
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0357 - accuracy: 0.9890
Epoch 7/10
1872/1875 [============================>.] - ETA: 0s - loss: 0.0272 - accuracy: 0.9919
Reached 99% accuracy so cancelling training!
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0272 - accuracy: 0.9919

Convolutions et regroupement

Si vous avez déjà travaillé avec le traitement d'images, vous avez peut-être rencontré le terme convolution. C'est une technique qui consiste à passer un filtre sur une image pour mettre en évidence certaines caractéristiques. Les réseaux neuronaux convolutionnels (CNN) utilisent les convolutions comme composant clé pour classer les images avec une grande précision.

Dans le contexte des CNN, les convolutions fonctionnent en faisant glisser un filtre (également connu sous le nom de noyau) sur l'image et en effectuant un produit scalaire entre le filtre et les pixels de la région actuelle. Ce processus est répété pour chaque pixel de l'image, créant une nouvelle image qui met en évidence certaines caractéristiques. Le filtre agit comme un ensemble de poids que le réseau apprend pendant l'entraînement, ce qui permet d'identifier les motifs dans les données qui sont pertinents pour la classification.

Mais comment exactement fonctionne la convolution ? Examinons cela de plus près.

Tout d'abord, nous définissons la taille du filtre. Une taille courante est 3x3, ce qui signifie que le filtre est une matrice 3x3 de valeurs. Pour chaque pixel de l'image, nous créons une grille 3x3 correspondante en incluant les voisins immédiats du pixel. Nous multiplions ensuite chaque valeur de la grille par la valeur correspondante dans le filtre et additionnons les résultats. Cela nous donne une nouvelle valeur pour le pixel, que nous pouvons utiliser pour créer une nouvelle image qui met en évidence certaines caractéristiques.

Par exemple, supposons que nous ayons une image d'une chaussure. Nous pouvons appliquer un filtre qui détecte les lignes verticales, ce qui pourrait être une caractéristique pertinente pour classer les chaussures. Le filtre pourrait ressembler à ceci:

 -1 0 1
-1 0 1
-1 0 1

Lorsque nous appliquons ce filtre à l'image de la chaussure, nous obtenons une nouvelle image qui met en évidence les lignes verticales de l'image. Cela peut faciliter la classification correcte de l'image par le réseau.

Bien sûr, les filtres peuvent être plus complexes que cela. Ils peuvent être plus grands ou plus petits, et ils peuvent avoir des valeurs différentes qui mettent en évidence différentes caractéristiques. En appliquant plusieurs filtres à une image, nous pouvons créer un ensemble de nouvelles images qui mettent chacune en évidence différentes caractéristiques. Ces nouvelles images peuvent être utilisées comme entrée pour le réseau, lui permettant d'identifier une plus grande variété de motifs pertinents dans les données.

Mais les convolutions ne sont qu'une partie de l'image. Une autre technique importante utilisée dans les CNN est le regroupement. Le regroupement consiste à prendre de petites grilles de pixels et à sélectionner la valeur maximale dans chaque grille. Cela a pour effet de réduire la taille de l'image tout en conservant les caractéristiques pertinentes qui ont été mises en évidence par les convolutions.

Par exemple, nous pourrions prendre une grille de pixels 2x2 et sélectionner la valeur maximale:

 [1 2]
[3 4]

Dans ce cas, nous choisirions la valeur 4 comme maximum. Ce processus est répété pour chaque grille de pixels, créant une nouvelle image qui est plus petite en taille mais contient toujours les caractéristiques pertinentes de l'image originale.

Combinées, les convolutions et le regroupement créent un outil puissant pour la classification des images. En appliquant des convolutions à une image, nous pouvons mettre en évidence les caractéristiques pertinentes qui sont importantes pour la classification. En appliquant le regroupement, nous pouvons réduire la taille de l'image tout en préservant ces caractéristiques. Cela permet aux CNN de classer les images avec une grande précision, ce qui en fait un outil précieux pour un large éventail d'applications.

Utilisation de tensorflow pour la convolution

Dans un exemple précédent, nous avons créé un réseau neuronal qui avait une couche d'entrée formée à nos données, une couche de sortie formée au nombre de catégories que nous voulions définir, et une couche cachée au milieu. Nous avons utilisé la fonction Flatten pour transformer nos images carrées de 28 par 28 en un tableau unidimensionnel.

Pour ajouter des convolutions à notre réseau, nous devons modifier notre code. Les trois dernières lignes sont les mêmes qu'avant, avec le Flatten, la couche cachée Dense avec 128 neurones et la couche de sortie Dense avec 10 neurones. Ce qui est différent, c'est ce que nous ajoutons au-dessus de cela.

Passons en revue le code ligne par ligne:

 model.add(Conv2D(64, (3,3), activation='relu', input_shape=(28,28,1)))

Ici, nous spécifions la première convolution. Nous demandons à Keras de générer 64 filtres pour nous. Ces filtres mesurent 3 par 3, leur activation est relu (ce qui signifie que les valeurs négatives seront supprimées), et la forme d'entrée est la même qu'avant, 28 par 28. Le "1" supplémentaire signifie que nous utilisons un seul octet pour la profondeur de couleur puisque notre image est en niveaux de gris.

Nous pouvons résumer :

Voici les paramètres :

Le nombre souhaité de convolutions à générer, de préférence une puissance de 2 à partir de 32, bien que le choix soit arbitraire.
La taille de la convolution, qui est une grille 3x3 dans ce cas.
La fonction d'activation choisie, qui dans ce cas est ReLU. Cette fonction renvoie x si x est supérieur à 0, et 0 sinon.

De plus, la forme des données d'entrée est spécifiée pour la première couche.

 model.add(MaxPooling2D(2,2))

Ensuite, nous ajoutons une couche MaxPooling. Cela réduit la dimensionnalité de la sortie de la couche précédente, ce qui facilite son traitement. Le paramètre 2 par 2 spécifie la taille de la fenêtre de pooling.

 model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dense(10, activation='softmax'))

Enfin, nous ajoutons la même fonction Flatten, la couche cachée Dense et la couche de sortie Dense qu'auparavant. La fonction Flatten transforme notre sortie en un tableau unidimensionnel, la couche cachée Dense a 128 neurones avec une fonction d'activation relu, et la couche de sortie Dense a 10 neurones avec une fonction d'activation softmax.

Vous vous demandez peut-être ce que sont les 64 filtres et comment ils sont générés. Cela va au-delà du cadre de cette classe d'entrer dans trop de détails, mais les filtres ne sont pas aléatoires. Ils commencent avec un ensemble de filtres connus et efficaces de manière similaire à l'ajustement de modèle que nous avons vu précédemment. Les filtres qui fonctionnent bien sont appris au fil du temps grâce à un processus appelé rétropropagation.

Utilisation de tensorflow pour le pooling

Afin d'optimiser davantage notre modèle CNN, nous pouvons ajouter des couches de convolution et de max-pooling supplémentaires au réseau. Après chaque couche de max-pooling, la taille de l'image est réduite, ce qui facilite le traitement par le réseau.

En utilisant la méthode model.summary, nous pouvons inspecter les couches du modèle et voir comment l'image est transformée à travers les convolutions. La colonne de forme de sortie peut être initialement déroutante, mais il est important de se rappeler que le filtre est un filtre 3 par 3. Lors du balayage d'une image en partant du haut à gauche, le premier pixel pouvant être calculé est celui qui possède les huit voisins qu'un filtre 3x3 nécessite. Cela signifie qu'une marge d'un pixel autour de l'image ne peut pas être utilisée, ce qui donne une sortie de la convolution qui est de deux pixels plus petite sur x et y.

Après chaque couche de max-pooling, la taille de l'image est réduite d'un facteur de deux. Par exemple, une image de 26 par 26 est réduite à 13 par 13 après la première couche de max-pooling, puis à 5 par 5 après la deuxième couche de max-pooling. Cela résulte en une couche aplatie avec 1 600 éléments, contre les 784 précédents. Le nombre de convolutions spécifié par image impactera ce nombre, ainsi que les autres paramètres définis lors de la définition des couches convolutionnelles 2D.

En expérimentant avec différents paramètres et nombres de convolutions, nous pouvons trouver le point idéal où le modèle est plus précis tout en s'entraînant plus rapidement. Le classeur offre une opportunité de l'essayer par nous-mêmes.

Voici un exemple complet :

 # Définir le modèle CNN
modèle = models.Sequential()
modèle.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
modèle.add(layers.MaxPooling2D((2, 2)))
modèle.add(layers.Conv2D(64, (3, 3), activation='relu'))
modèle.add(layers.MaxPooling2D((2, 2)))
modèle.add(layers.Conv2D(64, (3, 3), activation='relu'))
modèle.add(layers.Flatten())
modèle.add(layers.Dense(64, activation='relu'))
modèle.add(layers.Dense(10))

Après la couche de convolution, une couche MaxPool2D suit, qui sert à compresser l'image tout en préservant les caractéristiques mises en évidence. En spécifiant (2,2) pour le MaxPool2D, la taille de l'image est réduite à un quart de sa taille originale. Essentiellement, cela est fait en créant un tableau 2x2 de pixels et en sélectionnant le plus grand, réduisant ainsi 4 pixels en 1. Ce processus est répété sur toute l'image, réduisant à la fois le nombre de pixels horizontaux et verticaux de moitié, réduisant ainsi l'image à 25% de sa taille originale. Bien que les détails techniques de ce processus dépassent le cadre de cette discussion, l'effet global est de compresser l'image tout en conservant les caractéristiques clés mises en évidence par la convolution.

À propos du surajustement

Pour explorer davantage les résultats, vous pourriez essayer d'exécuter l'entraînement pendant environ 20 époques. Cependant, soyez conscient que bien que les résultats puissent initialement paraître bons, les résultats de validation peuvent diminuer en raison du surapprentissage. Le surapprentissage se produit lorsque le réseau devient trop spécialisé dans les données d'entraînement et est moins efficace pour interpréter de nouvelles données invisibles. C'est comme n'avoir jamais vu que des chaussures rouges de votre vie et être très bon pour les identifier. Mais quand vous voyez des chaussures en daim bleu, elles peuvent être déroutantes.

Pour visualiser les convolutions et le regroupement, vous pouvez imprimer les 100 premières étiquettes de l'ensemble de test, telles que l'index 0, 23 et 28, qui ont toutes la même valeur (c'est-à-dire 9), indiquant qu'elles sont toutes des chaussures. En exécutant la convolution sur chaque image, vous pouvez identifier les caractéristiques communes entre elles que la couche dense utilise probablement pour identifier les chaussures en fonction de cette combinaison de convolution / regroupement.

ImageDataGenerator

Jusqu'à présent, vous avez construit un classificateur d'images en utilisant un réseau neuronal profond et amélioré ses performances en ajoutant des convolutions. Cependant, le classificateur précédent était limité à un ensemble de données d'images uniformes, comme des vêtements de scène encadrés en 28 par 28 pixels. Maintenant, considérons un scénario où vous avez des images plus grandes avec différentes tailles, des rapports d'aspect et des emplacements de sujets variés, comme des images de chevaux et d'humains. De plus, les exemples précédents utilisaient un ensemble de données intégré avec des ensembles d'entraînement et de test prédivisés et des étiquettes disponibles. Cependant, dans de nombreux cas, vous devrez vous occuper vous-même de la préparation des données.

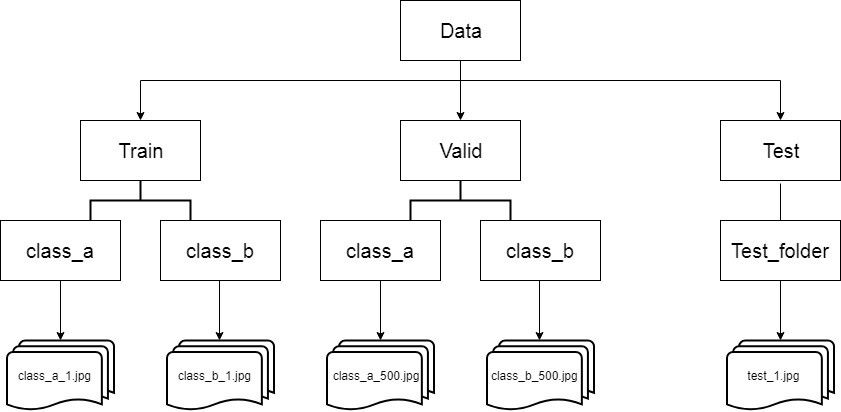
Pour répondre à ces défis, TensorFlow fournit des API utiles, comme le générateur d'images dans le module Keras.preprocessing.image. Une caractéristique notable du générateur d'images est sa capacité à générer automatiquement des étiquettes en fonction de la structure du répertoire. Par exemple, considérez une structure de répertoire avec un répertoire "images" contenant des sous-répertoires pour l'entraînement et la validation. Au sein de ces sous-répertoires, vous avez des répertoires "chevaux" et "humains" avec des images respectives. Le générateur d'images peut créer un alimenteur de données qui charge et étiquette automatiquement les images en conséquence. Lorsque vous pointez le générateur d'images sur le répertoire d'entraînement, les étiquettes seront "chevaux" et "humains", et il en sera de même lorsque vous le pointerez sur le répertoire de validation.

Voyons un exemple de comment utiliser le générateur d'images dans TensorFlow:

 from tensorflow.keras.preprocessing.image import ImageDataGenerator

# Instantiate the image generator
image_generator = ImageDataGenerator(rescale=1.0/255)

# Load and label images from the training directory
training_data_generator = image_generator.flow_from_directory(
    'path/to/training_directory',
    target_size=(300, 300),
    batch_size=32,
    class_mode='binary'
)

# Load and label images from the validation directory
validation_data_generator = image_generator.flow_from_directory(
    'path/to/validation_directory',
    target_size=(300, 300),
    batch_size=32,
    class_mode='binary'
)

Nous créons un objet ImageDataGenerator et spécifions rescale=1.0/255 pour normaliser les valeurs de pixel. Ensuite, nous utilisons la méthode flow_from_directory pour charger et étiqueter les images à partir des répertoires d'entraînement et de validation. Il est important de noter que lors de l'utilisation de flow_from_directory, vous devez pointer le générateur vers le répertoire contenant les sous-répertoires avec des images, plutôt que directement vers le sous-répertoire lui-même. Les noms de sous-répertoire seront utilisés comme étiquettes pour les images qu'ils contiennent.

Pour assurer des tailles d'entrée cohérentes pour entraîner un réseau neuronal, les images seront redimensionnées à la target_size spécifiée (dans ce cas, 300 par 300 pixels) au moment du chargement. Ce redimensionnement est fait automatiquement, vous n'avez donc pas besoin de prétraiter les images séparément.

Les images seront chargées par lots, où le paramètre batch_size détermine le nombre d'images dans chaque lot. Le choix de la taille du lot peut avoir un impact sur les performances, mais la détermination de la valeur optimale dépasse le cadre de cette explication.

Comme il s'agit d'un classificateur binaire (distinguant les chevaux et les humains), nous définissons class_mode='binary'. Pour la classification multiclasses, d'autres options seront explorées dans les parties ultérieures du cours.

Le processus pour le générateur de validation est similaire, sauf qu'il pointe vers le répertoire de validation et génère des étiquettes en conséquence.

Dans le cahier fourni, vous trouverez des instructions sur la manière de télécharger les images sous forme de fichier zip, de les trier dans les sous-répertoires d'entraînement et de test, et de les organiser dans les sous-répertoires "chevaux" et "humains". Ces étapes sont mises en œuvre en utilisant du Python pur et ne sont pas spécifiques à TensorFlow ou à l'apprentissage profond. Le cahier vous guidera tout au long du processus.

ConvNet pour utiliser des images complexes

Voici le code du réseau neuronal utilisé pour classer les chevaux par rapport aux humains, accompagné de quelques explications sur les différences par rapport au classificateur d'articles de mode précédent :

 import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Conv2D(16, (3, 3), activation='relu', input_shape=(300, 300, 3)),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Conv2D(32, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
    tf.keras.layers.MaxPooling2D(2, 2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(512, activation='relu'),
    tf.keras.layers.Dense(1, activation='sigmoid')
])

Dans ce réseau, nous avons trois ensembles de couches de convolution et de pooling en haut pour gérer la complexité et la taille plus élevées des images. Contrairement aux images précédentes de 28 par 28, nous commençons avec des images de 300 par 300 et réduisons progressivement leur taille à travers les convolutions et le pooling. La taille de l'image passe de 298 par 298 à 149 par 149, puis à 73 par 73, et enfin à 35 par 35. Ces convolutions aident à extraire les caractéristiques pertinentes des images.

La forme d'entrée du réseau est définie à (300, 300, 3), indiquant que nous attendons des images en couleur avec trois canaux (rouge, vert, bleu). Chaque canal est représenté par un octet, ce qui résulte en un motif couleur 24 bits courant.

La couche de sortie du réseau a également changé. Au lieu d'avoir un neurone par classe comme dans la classification multiclasse précédente, nous avons maintenant un seul neurone pour la tâche de classification binaire consistant à distinguer entre les chevaux et les humains. La fonction d'activation utilisée est sigmoid, adaptée à la classification binaire. Elle produit une probabilité entre 0 et 1, représentant la probabilité que l'image d'entrée appartienne à l'une ou l'autre classe.

En redimensionnant les images à 300 par 300 et en utilisant des convolutions, nous réduisons la dimensionnalité des données avant de les introduire dans les couches denses. La forme finale après l'aplatissement et les convolutions est (78 400), ce qui est nettement inférieur aux 90 000+ valeurs initiales si nous avions utilisé les images brutes de 300 par 300 sans convolutions. Cette réduction de la dimensionnalité aide à améliorer l'efficacité computationnelle et permet au réseau de se concentrer sur les caractéristiques pertinentes.

Vous pouvez expérimenter différentes architectures de réseau et paramètres dans le classeur pour voir comment ils affectent la performance du modèle sur la tâche de classification chevaux contre humains.

entraînement

Lorsqu'on traite des tâches de classification binaire, il est crucial de choisir des fonctions de perte et des optimiseurs appropriés. Dans l'exemple en question, nous nous éloignons de l'entropie croisée catégorielle et optons plutôt pour l'entropie croisée binaire. Ce choix s'harmonise mieux avec notre problème de classification binaire, permettant une formation et une évaluation plus précises du modèle.

De plus, nous introduisons l'optimiseur RMSprop, qui permet de régler finement le taux d'apprentissage pour expérimenter des améliorations de performance. Alors que l'optimiseur Adam était précédemment utilisé, essayer différents optimiseurs comme RMSprop peut aider à obtenir de meilleurs résultats selon la tâche et l'ensemble de données spécifiques.

Comprendre le Processus d'Entraînement

Nous rencontrons une approche d'entraînement légèrement différente par rapport à la méthode model.fit précédente. Au lieu de cela, nous utilisons un générateur, spécifiquement un générateur d'images, pour diffuser et traiter les données d'entraînement. Examinons les paramètres impliqués et leur signification.

Générateur d'Entraînement :

Nous utilisons un générateur d'entraînement pour diffuser les images à partir du répertoire d'entraînement. Vous vous souvenez de la taille du lot que vous avez définie lors de la création du générateur ? Elle joue un rôle vital dans les étapes suivantes. Par exemple, si nous définissons la taille du lot à 128 et avons un total de 1 024 images dans le répertoire d'entraînement, nous les chargerions en huit lots (128 images par lot).

Étapes par Époque :

Pour s'assurer que toutes les images du répertoire d'entraînement sont chargées pendant le processus d'entraînement, nous devons définir le paramètre steps_per_epoch en conséquence. Dans notre exemple, cette valeur serait de huit, représentant le nombre de lots nécessaires pour couvrir toutes les 1 024 images.

Prédiction du modèle :

Pour obtenir des prédictions à partir du modèle entraîné, le code utilise la fonction model.predict. En passant les détails de l'image en entrée, cette fonction renvoie un tableau de classes. Dans le cas d'une classification binaire, le tableau contiendra un élément, avec une valeur proche de 0 pour une classe et proche de 1 pour l'autre.

Changement de la taille de l'image et de l'architecture du modèle

Lors de la configuration initiale, nos images faisaient 300 par 300 pixels. Cependant, nous avons décidé de réduire la taille de l'image à 150 par 150 pixels, ce qui réduit efficacement le jeu de données à un quart de sa taille d'origine. Ce changement est effectué pour observer les conséquences sur l'entraînement et la précision de la classification. De plus, nous apportons des ajustements à l'architecture du modèle pour prendre en compte la forme d'entrée modifiée. Plus précisément, nous supprimons les quatrième et cinquième combinaisons de convolution et de max pool de l'architecture originale.

Entraînement et évaluation

Après avoir configuré le modèle avec l'architecture et la taille d'image modifiées, nous passons à l'entraînement et à l'évaluation. Le processus d'entraînement montre des résultats prometteurs, avec un entraînement rapide et des scores de précision et de validation raisonnablement bons. Il est important de noter que des valeurs de précision excessivement élevées, telles que 1,000, peuvent indiquer un surapprentissage, où le modèle performe exceptionnellement bien sur les données d'entraînement mais a du mal avec des données non vues.

Évaluation d'images du monde réel

Pour évaluer davantage les performances du modèle, nous le testons avec des images du monde réel. La première image, montrant une fille et un cheval, est toujours correctement classée comme un cheval. De même, une autre image d'un cheval est catégorisée avec précision. Ensuite, les images d'autres chevaux reçoivent également des classifications correctes. Cependant, une observation notable est faite avec une image d'une femme. Auparavant, en utilisant des images plus grandes de 300 par 300 pixels et plus de convolutions, le modèle la classait correctement. Cependant, avec la taille d'image réduite, le modèle la classe de manière incorrecte. Cela démontre l'importance d'évaluer les données d'entraînement avec un ensemble de validation complet, d'identifier les mauvaises classifications et d'explorer des améliorations potentielles.

Tensorflow - bases