FrançaisAlgorithmes d'apprentissage automatique
Au cours de cet article, nous allons apprendre à propos des algorithmes d'apprentissage automatique tels que :
- Apprentissage supervisé : c'est le type d'algorithme le plus utilisé dans les applications du monde réel. Ils ont des avancées plus rapides.
- Apprentissage non supervisé
- Systèmes de recommandation
- Apprentissage par renforcement
Nous allons passer par les différents sujets et essayer de les appliquer dans un contexte avec de nombreuses explications.
Apprentissage supervisé
Aujourd'hui, 99% de la valeur créée par l'apprentissage automatique est créée en utilisant l'apprentissage supervisé.
Régression
Expliquons cela :
Considérons pour éviter une entrée, appelée X, et une sortie appelée Y. Nous allons expliquer à la machine que nous nous attendons à avoir une variable Y, et pour la créer, nous créerons un algorithme qui aidera la machine à comprendre le besoin et comment le résoudre.
Ainsi, Y ici est une prédiction que la machine imagine être la valeur correcte. Prenons un exemple :
| Entrée(X) | Sortie(Y) | Application |
|---|---|---|
| spam?(0/1) | Filtrage de spam | |
| Audio | transcription de texte | Reconnaissance vocale |
| Anglais | Espagnol | Traduction automatique |
| Image, info radar | Position de l'autre voiture | Voiture autonome |
Nous avons ici quelques exemples d'applications d'entrée/sortie. L'idée principale est d'obtenir un résultat que nous connaissons déjà et de l'apprendre à la machine.
Après l'apprentissage sur l'exemple que vous avez fourni, pour une entrée de variable et une sortie de résultat, nous considérons que la formation est terminée. Par conséquent, l'IA devrait maintenant être capable de recevoir de nouvelles entrées et de déterminer les bonnes réponses (Y) par elle-même.
Imaginez que vous voulez prédire le prix d'une maison en fonction de sa taille ?
- Nous allons collecter des données existantes
- Nous allons tracer les données :
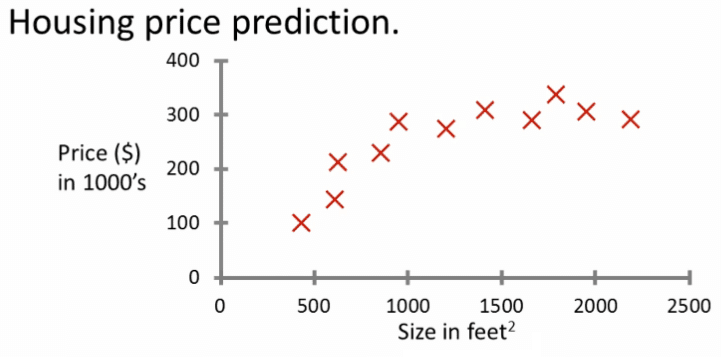
Avec ces données, nous avons des entrées et des sorties correctes, ce qui signifie que nous avons notre ensemble de données à fournir à l'IA.
Alors imaginez cette application, où nous voulons prédire le prix auquel nous vendrons une maison. Prenons un exemple :
- Le moyen le plus simple sera de dessiner une ligne droite entre les différentes valeurs, ce qui signifie que nous avons une moyenne du prix. Mais ce n'est pas ce que nous voulons, car il peut arriver que vous vendiez votre maison pour moins cher ou même pour plus cher et ne jamais la vendre.
- La façon la plus compliquée sera de créer une courbe, et d'inclure les valeurs les plus élevées pour avoir une idée du maximum que vous pouvez vendre. Ce qui réduira le risque, mais peut également réduire la rapidité de vente.
Voici deux approches pour vous montrer la décision que vous devez prendre pour percer avec le jeu de données parfait que vous pensez être meilleur pour l'apprentissage.
Pendant l'apprentissage supervisé, nous fournirons un algorithme appelé : la bonne réponse, qui est le prix correct Y donné pour chaque maison sur le terrain. Le rôle de cet algorithme sera de prédire le meilleur prix pour vendre votre maison. Ce type d'apprentissage supervisé est appelé Régression : nous essayons de prédire un nombre infiniment de nombres possibles.
Classification
Imaginez que vous avez des données de régression pour prédire la détection du cancer du sein:
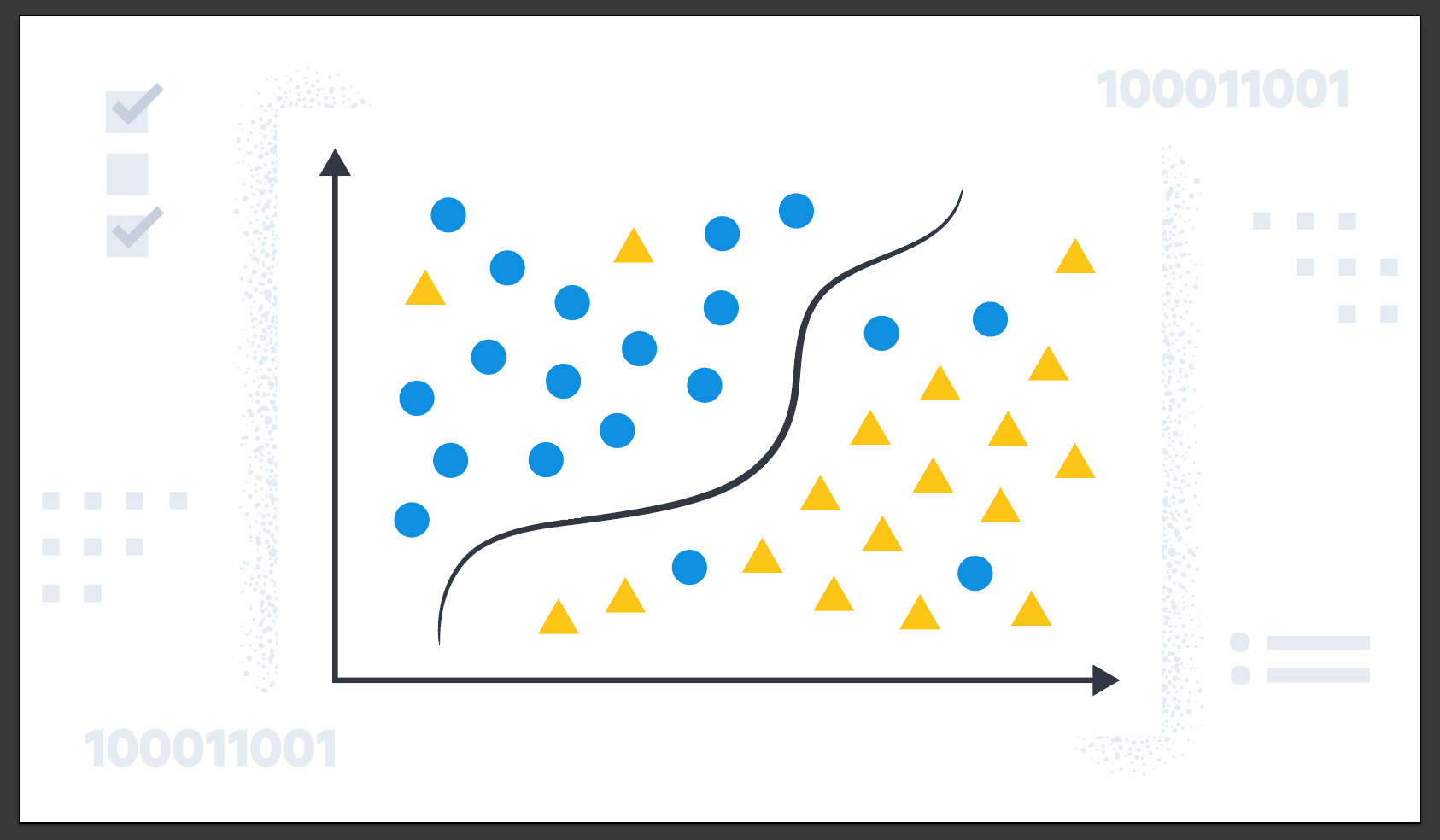
Cette IA sera importante pour un médecin afin de détecter un cancer plus tôt et de sauver quelqu'un qui en a besoin. Elle aidera à détecter si une tumeur qu'une bosse est maligne, c'est-à-dire cancéreuse ou dangereuse.
Vous devriez donc avoir des données qui entrent avec différentes tailles :
| Taille | Diagnostic |
|---|---|
| 2 | 0 |
| 5 | 1 |
| 1 | 0 |
| 7 | 1 |
- 0 signifie que c'est bénin
- 1 signifie que c'est malin
En utilisant ces données, nous pouvons créer un graphique, et vous verrez que la différence entre la régression sera que nous essayons de prédire de petits nombres : 2 résultats possibles dans ce cas. C'est différent de la régression, où nous essayons de prédire des nombres infinis, ici nous avons 2 solutions possibles.
Sur le graphique ci-dessous, vous voyez que nous utilisons des symboles pour représenter les données, il est plus facile pour nous d'avoir ce genre de représentativité.
Pendant la classification, vous pouvez avoir plus de 2 catégories de sortie possibles, peut-être que nous pouvons produire plusieurs cancers comme :
- Bénin
- Malin type 1
- Malin type 2
Dans ce cas, nous pouvons dire que la classification prédit des catégories qui n'ont pas de nombres. Comme, cette image est un chat ou un chien ? Il peut prédire un petit ensemble limité de catégories de sortie possibles telles que 0,1 et 2 mais pas tous les nombres possibles entre comme 0,5 ou 1,7.
Apprentissage non supervisé
L'apprentissage non supervisé est tout aussi super que l'apprentissage supervisé. Lorsque nous faisons de l'apprentissage supervisé, chaque entrée est liée à une valeur de sortie attendue. Dans cet apprentissage non supervisé, nous ne donnons pas de données qui sont associées à une sortie. Les données ne sont donc fournies qu'avec des entrées x, mais pas d'étiquettes de sortie y. L'algorithme doit trouver une structure dans les données.
Clustering
Nous allons essayer de trouver des éléments intéressants dans des données non étiquetées. Nous avons demandé à notre équipe de trouver par elle-même ce qui est intéressant ou les motifs ou structures qui pourraient être dans ces données. L'apprentissage non supervisé décidera si les données peuvent être attribuées à deux groupes différents ou deux clusters différents. Il pourrait donc décider qu'il y a un cluster qui se regroupe ici et un autre cluster ou groupe ici. Nous appelons ce type d'apprentissage non supervisé : algorithme de clustering.
Cet algorithme est utilisé par Google News : chaque jour, il cherche des centaines de nouvelles sur Internet et les regroupe. L'algorithme de clustering trouve des articles sur Internet, recherche des titres d'articles qui mentionnent un mot et regroupe simplement ces informations pour fournir un résultat.
Jetons un coup d'œil au clustering de données ADN, nous avons des personnes avec des informations spécifiques sur l'ADN, comme le gène de la couleur des yeux, etc. En mettant ces données dans un algorithme pour regrouper certaines informations qui sont proches les unes des autres, il crée par lui-même une structure pour chaque donnée ADN. Cela signifie que nous ne fournissons aucune sortie, le modèle crée lui-même les groupes en analysant les données fournies par X.
Détection d'anomalies
Elle est utilisée pour trouver des points de données inhabituels, cela s'avère vraiment important pour la détection de fraudes, où des événements inhabituels, des transactions inhabituelles pourraient être des signes de fraude.
Réduction de la dimensionnalité
Compresser les données en utilisant moins de nombres, et éviter de perdre le moins d'informations possible.
Notebooks Jupyter
C'est l'environnement par défaut que beaucoup d'entre nous utilisent pour coder, expérimenter et essayer des choses. Il fournit exactement le même environnement que les grandes entreprises utilisent dans le monde entier.
Modèle de régression linéaire
Vous avez introduit ce modèle précédemment, nous allons approfondir le modèle et essayer de fournir des exemples dont nous aurons besoin.
C'est probablement l'algorithme d'apprentissage le plus largement utilisé dans le monde aujourd'hui. Commençons par un problème que vous pouvez résoudre à l'aide de la régression linéaire. Disons que vous voulez prédire le prix d'une maison en fonction de la taille de la maison.
Nous avons reçu cet ensemble de données d'une agence qui vend des maisons. Ici, chaque point de données, chaque petite croix, représente une maison avec la taille et le prix pour lequel elle a été vendue le plus récemment. Disons maintenant que vous êtes un agent immobilier et que vous aidez un client à vendre sa maison. Elle vous demande : combien pensez-vous que je peux obtenir pour cette maison ? Cet ensemble de données pourrait vous aider à estimer le prix qu'elle pourrait obtenir pour sa maison.
Vous savez que la maison fait 1250 pieds carrés, nous pouvons créer un modèle de régression linéaire à partir de cet ensemble de données. Votre modèle ajustera une ligne droite aux données, qui pourrait ressembler à ceci. Sur la base de cela, vous tracez une ligne verticale sur l'axe des ordonnées à gauche, vous pouvez voir que le prix est peut-être autour d'ici, disons environ 220 000 $. C'est un exemple, et linéaire est juste un exemple pour prédire une plage de nombres possibles.
Voici un exemple de données :
| Taille en pieds² | Prix en 1000$ |
|---|---|
| 2104 | 400 |
| 1416 | 232 |
| 1534 | 315 |
| ... | |
| 3210 | 870 |
Ici, vous avez des entrées et des sorties, à partir de données réelles pour définir nos données à ingérer et les graphiques pour les prédictions. Il sera utilisé pour former le modèle et il s'appelle : l'ensemble d'entraînement. C'est donc le support du modèle, ou un ensemble d'entrées, appelé X : toutes les valeurs sur "Taille en pieds²" sont une valeur X, où le prix en 1000 $ est la variable de sortie Y.
Pour concevoir une ligne, nous appellerons une variable M, où M(i) = (X(i), y(i)) pour concevoir une ligne spécifique.
Pour former notre modèle, nous suivrons les étapes suivantes :
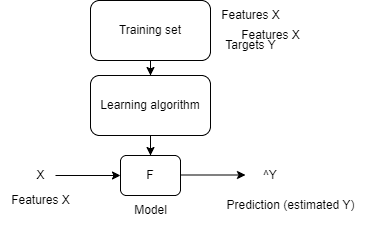
- Notre ensemble d'entraînement est défini
- Nous passons cet ensemble d'entraînement à un algorithme d'apprentissage
- La sortie de l'apprentissage sera le modèle défini qui peut prédire des données en y insérant une entrée
- ^Y est la prédiction
Nous pouvons ainsi créer la fonction comme ceci :
- W est le nombre de fois utilisé pour l'entrée X, c'est le poids
- B est le biais
C'est la fonction pour prédire une ligne, ici c'est une façon linéaire, qui est plus facile que la courbe pour la prédiction.
Illustrons cela en utilisant le code :
Nous utiliserons numpy pour créer notre modèle et afficher notre graphique avec matplotlib.
Ensuite, nous allons créer l'ensemble d'entraînement pour nos données en faisant ceci :
import numpy as np
import matplotlib.pyplot as plt
# x_train is the input variable (size in 1000 square feet)
# y_train is the target (price in 1000s of dollars)
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train = {x_train}")
print(f"y_train = {y_train}")
Vous utiliserez m pour désigner le nombre d'exemples d'entraînement. Les tableaux numpy ont un paramètre .shape. x_train.shape renvoie un tuple python avec une entrée pour chaque dimension. x_train.shape[0] est la longueur du tableau et le nombre d'exemples, comme illustré ci-dessous.
# m is the number of training examples
print(f"x_train.shape: {x_train.shape}")
m = x_train.shape[0]
print(f"Number of training examples is: {m}")
# m is the number of training examples
m = len(x_train)
print(f"Number of training examples is: {m}")
Ensuite, nous pouvons tracer nos données en utilisant notre bibliothèque :
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()
Le tracé est défini, nous pouvons maintenant définir notre fonction qui calculera notre modèle et renverra la sortie :
def compute_model_output(x, w, b):
"""
Computes the prediction of a linear model
Args:
x (ndarray (m,)): Data, m examples
w,b (scalar) : model parameters
Returns
y (ndarray (m,)): target values
"""
m = x.shape[0]
f_wb = np.zeros(m)
for i in range(m):
f_wb[i] = w * x[i] + b
return f_wb
Nous appliquons notre fonction : 𝑓𝑤,𝑏(𝑥(𝑖)) où nous pouvons écrire :
- pour 𝑥(0), f_wb = w * x[0] + b
- pour 𝑥(1), f_wb = w * x[1] + b
Maintenant, ajoutons notre fonction et compilons-la :
tmp_f_wb = compute_model_output(x_train, w, b,)
# Plot our model prediction
plt.plot(x_train, tmp_f_wb, c='b',label='Our Prediction')
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r',label='Actual Values')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()
Nous devrions afficher le résultat de notre graphique comme ceci :
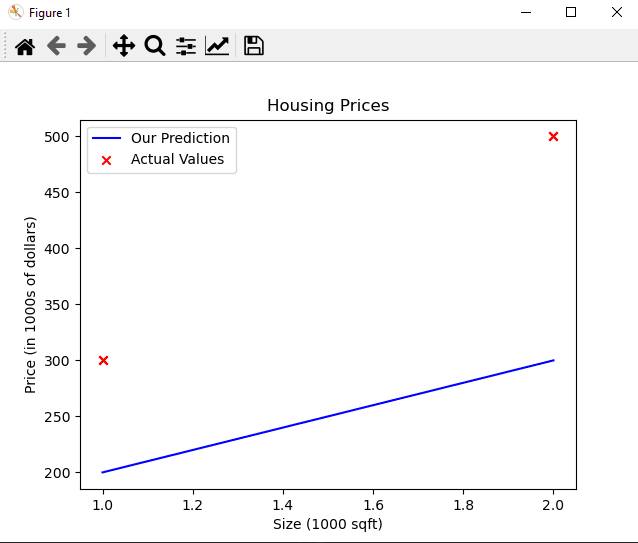
Comme vous pouvez le constater, en fixant $w = 100$ et $b = 100$, cela ne donne pas une ligne qui convient à nos données.
Maintenant que nous avons un modèle, nous pouvons l'utiliser pour faire des prédictions. Prédisons le prix d'une maison de 1200 pieds carrés. Puisque les unités de 𝑥 sont en milliers de pieds, 𝑥 vaut 1,2.
w = 200
b = 100
x_i = 1.2
cost_1200sqft = w * x_i + b
print(f"${cost_1200sqft:.0f} thousand dollars")
Voici ce que devrait être le résultat en sortie :
x_train = [1. 2.]
y_train = [300. 500.]
x_train.shape: (2,)
Number of training examples is: 2
Number of training examples is: 2
(x^(0), y^(0)) = (1.0, 300.0)
w: 100
b: 100
$340 thousand dollars
Vous pouvez trouver le code ici : Github - linear regression
Fonction de coût
Cette fonction indique à quel point le modèle se comporte bien, en fonction de laquelle nous pourrons l'ajuster pour le faire mieux.
| Taille en pieds carrés (caractéristiques) | Prix en 1000$ (cibles) |
|---|---|
| 2104 | 400 |
| 1416 | 232 |
| 1534 | 315 |
| ... | |
| 3210 | 870 |
Le modèle utilisera ces données pour entraîner son modèle et utilisera cette formule :
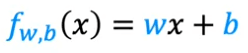
w,b : sont les paramètres utilisés pendant l'entraînement. Expliquons-le, il est possible d'avoir plusieurs graphes que nous définissons avec ces paramètres :
| w | b | résultat | Explication |
|---|---|---|---|
| 0 | 1.5 | F(x) = 0*X +1.5 = 1.5 | La prédiction est 1.5 (^y) |
| 0.5 | 0 | F(x) = 0.5*X +0 | La pente est de 0,5, car X sera notre valeur à calculer, la valeur peut varier |
| 0.5 | 1 | F(x) = 0.5*X +1 | La pente est de 0,5, car X sera notre valeur à calculer peut varier |
Lorsque nous définissons un graphique et que nous voyons une ligne passer près de notre valeur ou à travers comme ceci :
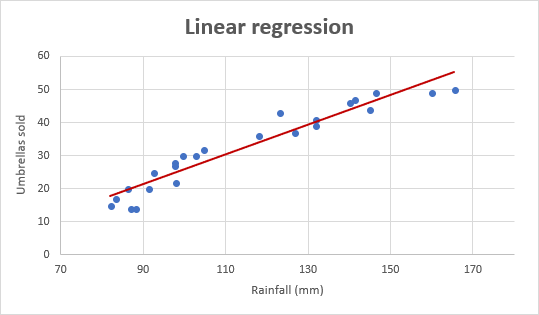
Vous pouvez penser que cela signifie que la ligne définie par f passe approximativement à travers ou près des exemples d'entraînement par rapport aux autres lignes possibles qui ne sont pas aussi proches de ces points.
La question sera comment puis-je trouver des valeurs pour W et B ?
Lorsque nous appliquons notre formule :
- Chaque point sur le graphique est une itération appelée "i"
- Lorsque nous pouvons dire que la formule devient :
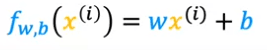
Nous devrons mesurer à quel point une ligne s'adapte aux données d'entraînement, pour ce faire, nous créons une "fonction de coût" : La fonction de coût prend la prédiction y hat et la compare à la cible y en prenant y hat moins y. Nous appelons cette différence : l'erreur, où nous mesurons à quelle distance la prédiction est de la cible.
Calculons le carré de cette erreur et nous voudrons calculer ce terme pour différents exemples d'entraînement i dans l'ensemble d'entraînement. Par exemple : nous calculerons ce terme d'erreur au carré.
Nous allons sommer de i = 1,2,3 jusqu'à m et nous rappeler que m est le nombre d'éléments d'entraînement, donc si :
- Remarquez que si nous avons plus d'exemples d'entraînement, m est plus grand et votre fonction de coût calculera un nombre plus grand.
Nous pouvons prédire cette fonction de coût comme ceci :
Pour construire une fonction de coût qui n'est pas affectée par la taille de l'ensemble d'entraînement, nous utiliserons l'erreur carrée moyenne comme mesure de performance, plutôt que l'erreur carrée totale. Pour ce faire, nous diviserons l'erreur carrée totale par le nombre d'exemples d'entraînement, représenté par la variable m. Cela garantira que la fonction de coût reste cohérente lorsque la taille de l'ensemble d'entraînement change.
La fonction de coût couramment utilisée en apprentissage automatique est généralement divisée par 2 fois le nombre d'exemples d'entraînement, représenté par la variable m. Cette division supplémentaire par 2 est effectuée pour des raisons mathématiques lors de calculs ultérieurs, cependant, elle n'est pas nécessaire pour que la fonction fonctionne correctement. Cette fonction de coût est appelée J(w,b), également connue sous le nom de fonction de coût de l'erreur quadratique, car elle implique la prise du carré des termes d'erreur. Bien que différentes fonctions de coût puissent être utilisées pour différentes applications en apprentissage automatique, la fonction de coût d'erreur quadratique est un choix largement utilisé et préféré pour la régression linéaire et d'autres problèmes de régression, car elle a montré de bons résultats dans de nombreuses applications.
Enfin, notre formule ressemble à ceci :
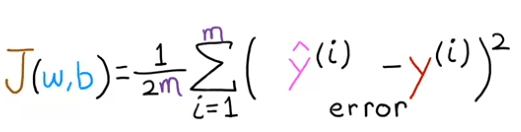
Nous appelons cette fonction de coût : Fonction de coût de l'erreur quadratique.
Ainsi, pour récapituler :
- Modèle :
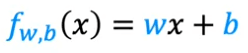
- Paramètres :
W,B. Il définira la ligne de notre graphique et nous voulons définir la valeur correcte pour W,B pour nous assurer que cette ligne correspond à nos données ou est la plus proche possible. Nous avons besoin de la fonction de coût.
- Fonction de coût :
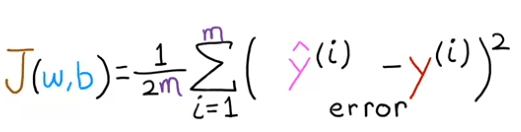
Le but est d'avoir J(w,b) le plus petit possible.
Nous pouvons simplifier nos équations :
- Modèle :
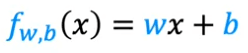
Vous pouvez visualiser ce processus en simplifiant le modèle original sur le côté gauche en supprimant le paramètre b, ou en le fixant à zéro. Cela signifie que b n'apparaît plus dans l'équation et que f(x) est maintenant simplement représenté par w fois x.
- Paramètres :
W, B. deviennent W du fait que nous avons enlevé "B".
- Fonction de coût :
Lorsque le paramètre b est fixé à zéro, le modèle devient plus simple, car il n'a plus qu'un seul paramètre, w. Le but du modèle est de trouver la valeur de w qui minimise J(w). Cette simplification est visualisée par le fait que la ligne définie par f(x) passe maintenant par l'origine. En examinant le graphique du modèle f(x) et de la fonction de coût J côte à côte, vous pouvez observer comment les deux sont liés. Avec le modèle simplifié, il est important de noter que bien que la valeur estimée de y dépende de la valeur de l'entrée x, la fonction de coût J dépend de la valeur de w, qui contrôle la pente de la ligne définie par f(x).
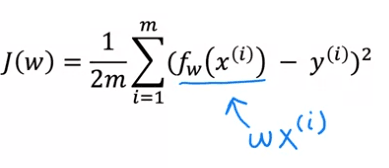
Examinons comment la fonction de coût varie lorsque différentes valeurs sont choisies pour le paramètre w. Pour ce faire, nous allons tracer les graphiques du modèle f(x) et de la fonction de coût J ensemble. Cela nous permettra de voir comment les deux sont liés et comment la fonction de coût change lorsque la valeur de w change.
Tout d'abord, il est important de noter que lorsque le paramètre w est fixé, f(w) ne dépend que de la variable d'entrée x. Cela signifie que la valeur prédite de y est déterminée par la valeur de x. D'autre part, la fonction de coût J dépend du paramètre w, qui contrôle la pente de la ligne définie par f(w). En d'autres termes, le coût défini par J est affecté par la valeur de w, car c'est une fonction de w.
Par exemple, considérons que la valeur de w est de 1. Pour ce choix, la fonction f(w) donnerait une ligne droite avec une pente de 1. Pour évaluer la fonction de coût, nous pouvons calculer J(w=1) qui est le coût de cette valeur particulière de w.
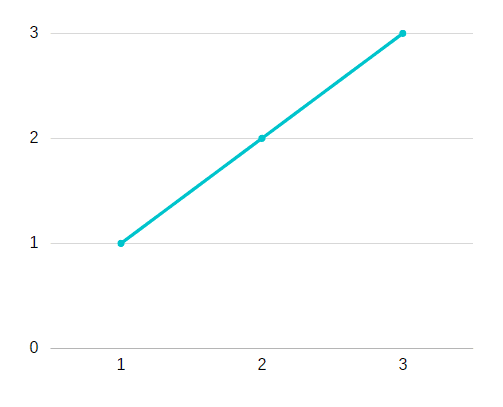
Prenons notre fonction de coût :
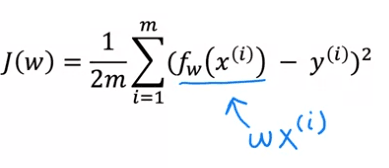
- Si W est égal à 1, nous pouvons le fournir, car fw sera égal à un.
- Si X et Y sont 1,2,3 ensemble comme sur le graphique, cela coûte 0 :
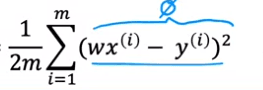3. Ainsi, pour les 3 exemples, le coût J est égal à 0.
Pour mieux comprendre comment la fonction de coût J(w) varie en fonction du choix de w, nous pouvons tracer J(w) en fonction de w. Étant donné que J est une fonction de w, l'axe horizontal sera étiqueté w au lieu de x et l'axe vertical sera étiqueté J au lieu de y.
Par exemple, si nous fixons w à 1, nous pouvons calculer le coût correspondant J(w=1) qui serait égal à 0, et le tracer sur le graphique. Nous pouvons également considérer différentes valeurs de w, telles que des valeurs négatives, zéro et positives, et observer comment f(x) et J(w) changent. Par exemple, lorsque w=0,5, f(x) est maintenant une ligne avec une pente de 0,5 et nous pouvons calculer le coût J(w=0,5). De cette manière, nous pouvons comparer les différentes f(x) et J(w) correspondant à différentes valeurs de w.
Nous examinons comment la fonction f(x) et la fonction de coût J(w) varient lorsque le paramètre w change. Le paramètre w peut prendre une gamme de valeurs, y compris des valeurs négatives, zéro et positives. Nous pouvons observer comment ces fonctions changent en les représentant avec différentes valeurs de w. Par exemple, si nous fixons w à 0,5, la fonction f(x) est une ligne avec une pente de 0,5 et nous pouvons calculer le coût J(w=0,5). La fonction de coût J(w) mesure la différence entre les valeurs prédites par f(x) et les valeurs réelles pour chaque exemple dans l'ensemble de données. Cette différence peut être visualisée comme la hauteur de la ligne verticale dans le graphique, représentant l'écart entre la valeur réelle de y et la valeur prédite par la fonction f(x) pour une valeur donnée de x.
Voici la représentation graphique :
Nous avons la ligne et pour définir la valeur de X, nous allons vérifier la différence entre notre ligne et l'objectif comme suit :
- (0,5-1)² + (1-2)² + (1,5-3)²
- J(0,5) = 1/2m[(0,5-1)² + (1-2)² + (1,5-3)² ]
- Comme nous avons 3 exemples d'entraînement : m=3
- (1/2*3)[3,5]
- Nous pouvons donc dire que 3,5/6 = 0,58 pour le coût J.
Remarque : w peut être une valeur négative !
Nous pouvons continuer à évaluer la fonction de coût J(w) pour différentes valeurs du paramètre w et les tracer. De cette manière, nous pouvons créer une représentation visuelle de la manière dont la fonction de coût change pour différentes valeurs de w. Ainsi, nous pouvons comprendre la forme de la fonction de coût J(w) et comment elle se comporte lorsque nous changeons la valeur du paramètre. Ce processus nous donne un moyen de déterminer la meilleure valeur du paramètre w qui minimise la fonction de coût J(w) et optimise le modèle.
Dans ce contexte, quelle est la méthode pour choisir la valeur du paramètre w qui permet à la fonction f de bien s'adapter aux données ? Une approche consiste à choisir la valeur de w qui donne la plus petite valeur possible de la fonction de coût J(w). Comme J(w) mesure les erreurs quadratiques entre les valeurs prédites et réelles, minimiser cette valeur permettra d'obtenir un modèle d'ajustement plus précis.
L'objectif principal de la régression linéaire est de déterminer les valeurs des paramètres tels que w, ou w et b qui minimisent la fonction de coût J(w). Cela est fait afin que la fonction f(x) générée par le modèle approche au mieux les valeurs réelles dans l'ensemble de données donné.
Prenons un exemple en utilisant numpy :
Supposons que nous souhaitons développer un modèle qui peut prédire le prix d'une maison en fonction de sa taille. Pour illustrer cela, utilisons deux points de données d'exemple : une maison de 1000 pieds carrés vendue pour 300 000 $, et une maison de 2000 pieds carrés vendue pour 500 000 $.
Considérons cet ensemble de données :
| Taille (1000 pieds carrés) | Prix (1000 $) |
|---|---|
| 1 | 250 |
| 1,7 | 290 |
| 2,0 | 430 |
| 2,5 | 475 |
| 3,0 | 622 |
| 3,2 | 720 |
Voici le code pour cette fonction de coût, en utilisant Python : 𝐽(𝑤,𝑏)=1/2𝑚∑𝑖=0𝑚−1(𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))²
def compute_cost_function(x, y, w, b):
"""
Calculate the cost function for linear regression.
The difference between the target (the value from our test) and the prediction is calculated and squared.
Args:
x (ndarray (m,)): Data, m examples
y (ndarray (m,)): target values
w,b (scalar) : model parameters
Returns
total_cost (float): The cost of using w,b as the parameters for linear regression
to fit the data points in x and y
"""
# number of training examples
m = x.shape[0]
cost_sum = 0
for i in range(m):
#f_wb is a prediction calculated
f_wb = w * x[i] + b
cost = (f_wb - y[i]) ** 2
cost_sum = cost_sum + cost
total_cost = (1 / (2 * m)) * cost_sum
return total_cost
Maintenant que nous avons cette fonction de coût, nous pouvons initialiser nos données :
#size in 1000 square feet
x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
#price in 1000 square in dollar
y_train = np.array([250, 290, 475, 430, 622, 720,])
# Initialize model parameters
w = 0
b = 0
# Compute the cost
cost = compute_cost_function(x_train, y_train, w, b)
print("Initial cost: ", cost)
# Create a grid of (w,b) values
ws = np.linspace(-50, 50, 100)
bs = np.linspace(-100000, 100000, 100)
W, B = np.meshgrid(ws, bs)
# Compute the cost for all (w,b) values
Z = np.array([compute_cost_function(x_train, y_train, w_i, b_i) for w_i, b_i in zip(np.ravel(W), np.ravel(B))])
# Reshape the cost array to match the shape of (w,b)
Z = Z.reshape(W.shape)
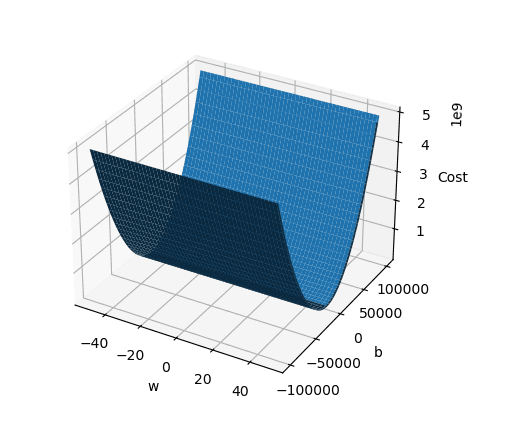
Nous avons calculé la fonction de coût pour notre prix, nous pouvons maintenant changer la valeur de W et de B comme mentionné précédemment. Visualisons cela dans un graphique :
# Create a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("Cost")
ax.plot_surface(W, B, Z)
plt.show()
Résultat :
