Introduction

Dans le vaste domaine de l'analyse de données et de l'apprentissage automatique, la compréhension des séquences et des données de séries temporelles constitue une compétence essentielle, ouvrant la voie à des prédictions robustes et précises. Dans les domaines de la finance, de la prévision météorologique, de l'économie ou même des soins de santé, notre capacité à comprendre l'ordre chronologique des événements et à discerner les motifs au fil du temps peut considérablement améliorer les processus de prise de décision.

Le monde intrigant des séquences, des séries temporelles et des prédictions attire, offrant un mélange de statistiques, d'apprentissage automatique et de compréhension approfondie des motifs temporels. Cet article se penchera sur ces domaines interconnectés, examinant comment ils fonctionnent individuellement et de manière symbiotique pour permettre une analyse sophistiquée et des prévisions fiables dans de nombreuses disciplines.

Nous explorerons le voyage fascinant des séquences simples, découvrirons la riche complexité des données de séries temporelles et arriverons à la tâche cruciale de la prédiction, l'acte de prédire l'avenir en fonction des motifs du passé. Que vous soyez un data scientist chevronné, un analyste en herbe ou simplement un lecteur curieux, préparez-vous à une exploration éclairante de ces puissants outils analytiques. Attachez-vous pour un voyage à travers le temps, où les points de données servent de pierres de touche vers l'avenir.

Séries temporelles

Lorsque nous regardons le monde qui nous entoure, nous observons souvent des motifs qui se répètent au fil du temps - les saisons qui changent, la montée et la chute des prix des actions, le flux et le reflux des marées ou même nos routines quotidiennes. Cette danse rythmique de répétition et de progression se reflète dans ce que nous appelons une série temporelle.

Une série temporelle est une collection de points de données répertoriés ou indexés dans une séquence chronologique. Les données sont généralement enregistrées à des intervalles réguliers et équidistants. Ces intervalles peuvent être chaque minute, chaque heure, chaque jour, chaque mois, voire chaque année.

Une série temporelle peut être univariée ou multivariée. Lorsque nous enregistrons une seule variable au fil du temps, nous l'appelons une série temporelle univariée. Par exemple, si nous suivions la température quotidienne pendant un an, nous obtiendrions une série temporelle univariée de températures.

Cependant, lorsque nous surveillons plus d'une variable au fil du temps, nous obtenons une série temporelle multivariée. Un exemple serait si nous enregistions à la fois la température quotidienne et les précipitations pendant un an. Ici, la température et les précipitations sont les variables, et ensemble, elles forment une série temporelle multivariée.

Comment cela fonctionne-t-il avec l'apprentissage automatique ?

Alors, qu'a à voir l'apprentissage automatique avec les séries temporelles ? En réalité, il existe un vaste champ de possibilités que nous pouvons explorer en utilisant l'apprentissage automatique sur des données de séries temporelles.

L'application la plus évidente est la prédiction ou la prévision de valeurs futures en fonction des données existantes. Prenons le graphique des taux de natalité et de mortalité pour le Japon. La prédiction des valeurs futures dans ce scénario peut être incroyablement utile pour les agences gouvernementales. De telles prédictions aident à planifier une multitude d'impacts sociétaux, tels que les politiques de retraite et les tendances en matière d'immigration.

Mais l'utilisation de l'analyse de séries temporelles ne se limite pas à la prévision de valeurs futures. Il y a des moments où nous pourrions vouloir regarder en arrière, pour reconstituer des points de données passés et comprendre la trajectoire historique qui nous a conduits à notre état actuel. Ce processus est connu sous le nom d'imputation.

L'imputation peut nous aider à dresser un tableau plus complet du passé, même lorsque certaines données sont manquantes. Prenons notre graphique de la loi de Moore, par exemple :

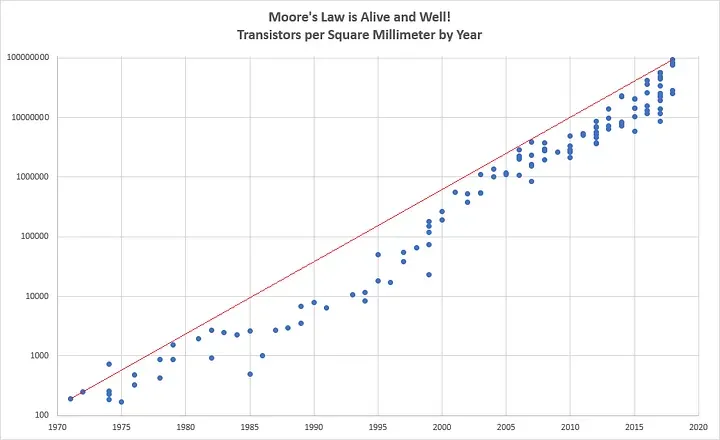
Vous avez peut-être remarqué des lacunes dans certaines années où aucune donnée n'était disponible car aucun circuit intégré n'a été publié. Grâce à l'imputation, nous pouvons combler ces lacunes et obtenir une compréhension plus complète des données.

Au-delà de ces applications, la prédiction de séries temporelles peut également servir d'outil précieux pour la détection d'anomalies. Par exemple, imaginez l'analyse des journaux de sites web ; une augmentation soudaine dans une série temporelle pourrait indiquer une éventuelle attaque de déni de service.

Enfin, l'analyse de séries temporelles peut également être utilisée pour identifier des motifs au sein de la série, nous aidant à comprendre les mécanismes sous-jacents qui ont généré la série. Une application classique de cela se trouve dans la reconnaissance vocale, où nous analysons des ondes sonores (qui sont un type de série temporelle) pour identifier des mots ou des sous-mots. En formant un réseau neuronal sur ces données de séries temporelles, nous pouvons développer des systèmes qui reconnaissent et retranscrivent avec précision la parole.

En essence, l'apprentissage automatique a un potentiel profond pour transformer notre compréhension et notre utilisation des données de séries temporelles, de la prédiction et de l'imputation à la détection d'anomalies et à la reconnaissance de motifs.

Motifs courants

Les données de séries temporelles se présentent sous une myriade de formes, chacune portant des motifs et des récits uniques. Il est bénéfique de pouvoir identifier ces motifs car cela nous aide à comprendre les données et à faire des prédictions précises. Alors, plongeons dans certains des motifs les plus courants que nous rencontrons dans l'analyse de séries temporelles.

Tendance

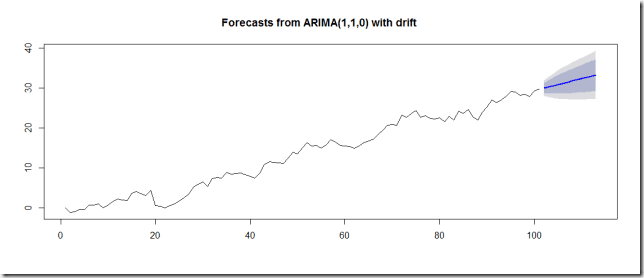
Le premier motif que nous voyons souvent est une tendance, où la série temporelle évolue dans une direction spécifique. Un exemple classique de cela serait notre discussion précédente sur la loi de Moore, qui montre une tendance à la hausse constante.

Saisonnalité

Un autre motif courant est la saisonnalité, où une série temporelle se répète à des intervalles prévisibles. Un exemple clair de cela peut être observé dans les données d'activité utilisateur d'un site web de développement de logiciels, qui présente des baisses régulières - des pics pendant les jours de semaine et des creux pendant les week-ends, illustrant un fort cycle hebdomadaire.

Certaines séries temporelles présentent un mélange de tendance et de saisonnalité. Par exemple, une série temporelle peut avoir une tendance générale à la hausse mais contenir des pics et des creux locaux correspondant aux changements saisonniers.

Bruit blanc

Cependant, toutes les séries temporelles ne sont pas prévisibles ou ne contiennent pas de motifs discernables. Certaines sont un assortiment aléatoire de valeurs, phénomène appelé 'bruit blanc'. Avec ce type de données, la prévision ou la prédiction est quasiment impossible.

Autocorrélées

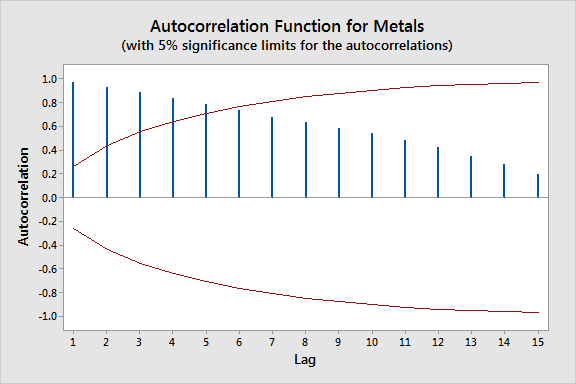
Un type intrigant de série temporelle est celle qui semble aléatoire avec des pics soudains, mais qui, à examen plus attentif, montre un motif autocorrélé. Dans de tels cas, la valeur à chaque étape temporelle dépend des valeurs précédentes. Ces séries, dites ayant une 'mémoire', contiennent souvent des pics imprévisibles ou des 'innovations'.

Les séries temporelles de la vie réelle présentent généralement un mélange de tendance, de saisonnalité, d'autocorrélation et de bruit. En identifiant ces motifs, les modèles d'apprentissage automatique peuvent effectuer des prédictions significatives, en supposant que l'avenir suive les mêmes motifs que le passé.

Mélange de motifs

Cependant, les séries temporelles peuvent être compliquées, modifiant considérablement leur comportement au fil du temps. De telles séries, appelées séries temporelles non stationnaires, posent un défi unique. Par exemple, une série peut présenter une tendance positive et une saisonnalité claire jusqu'à un certain point, puis changer complètement de comportement, montrant une tendance à la baisse sans saisonnalité discernable.

Dans ces scénarios, il est souvent plus efficace de former nos modèles sur une période limitée et récente de la série temporelle plutôt que sur l'ensemble de la série. Cela constitue une déviation de l'approche traditionnelle de l'apprentissage automatique où plus de données sont considérées comme meilleures. Dans l'analyse de séries temporelles, la valeur des données dépend souvent de la stationnarité de la série (son comportement ne change pas au fil du temps) ou de sa non-stationnarité.

Division des données

Maintenant que nous nous sommes familiarisés avec les motifs courants dans les séries temporelles, explorons les méthodologies que nous pouvons utiliser pour les prévoir. Nous commencerons par une série temporelle réaliste qui intègre une tendance, une saisonnalité et du bruit.

Une manière simple de prévoir est de prédire que la prochaine valeur sera identique à la dernière, une méthode connue sous le nom de prévision naïve. Malgré sa simplicité, cette approche peut fournir une ligne de base décente. Cependant, pour évaluer notre modèle de prévision, nous avons besoin de techniques plus sophistiquées.

Une méthode populaire s'appelle la partition fixe. Nous divisons généralement la série temporelle en trois segments : une période d'entraînement, une période de validation et une période de test. Si la série temporelle présente une saisonnalité, nous visons à nous assurer que chaque période contient un nombre entier de saisons (par exemple, une, deux ou trois années si la série présente une saisonnalité annuelle). Cela peut sembler différent de la manière dont nous partitionnons généralement les données pour les ensembles de données non temporelles, mais cela sert efficacement le même objectif.

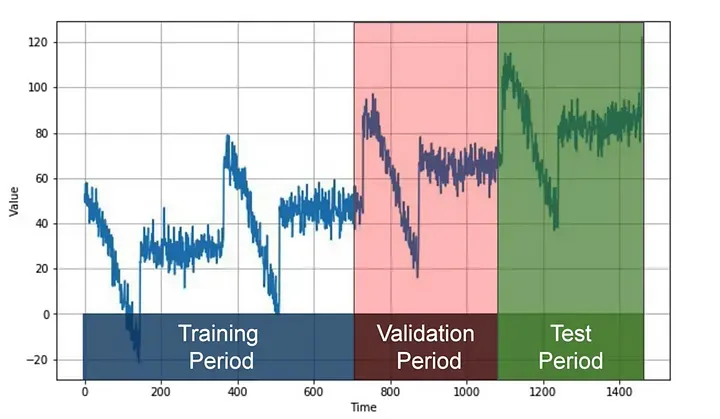
Le modèle est formé sur la période d'entraînement et évalué sur la période de validation. C'est là que nous pouvons expérimenter pour trouver la bonne architecture de modèle et ajuster les hyperparamètres jusqu'à ce que nous obtenions des performances souhaitables. Une fois que nous avons fait cela, nous re-formons souvent le modèle en utilisant à la fois les données d'entraînement et de validation, puis le testons sur la période de test.

Curieusement, après les tests, il n'est pas rare de reformer le modèle en utilisant également les données de test. Pourquoi ? Parce que les données de test, étant les plus récentes, fournissent souvent le signal le plus fort pour prédire les valeurs futures. En fait, certains peuvent même renoncer complètement à l'ensemble de test et former le modèle en n'utilisant que les périodes d'entraînement et de validation, le futur servant de jeu de test.

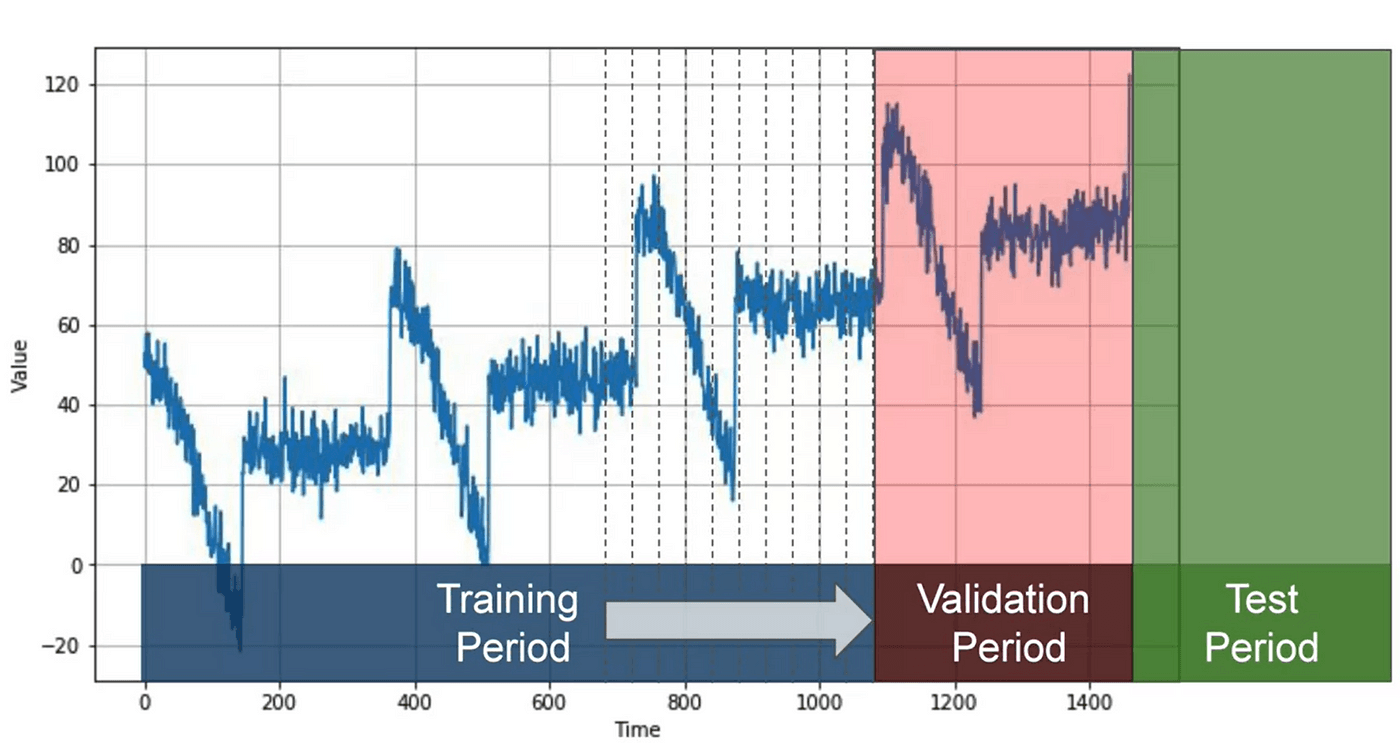
Une autre approche de la partition est appelée partitionnement en avant. Cela implique de commencer par une courte période d'entraînement et de l'augmenter progressivement à intervalles réguliers, comme quotidiens ou hebdomadaires. À chaque itération, le modèle est formé sur la période d'entraînement et utilisé pour prévoir l'unité de temps suivante dans la période de validation. On peut voir cela comme faisant la partition fixe plusieurs fois, affinant continuellement le modèle dans le processus.

Évaluation des performances

Une fois que nous avons établi notre modèle et partitionné nos données en périodes distinctes, l'étape suivante consiste à évaluer la performance du modèle. Pour cela, nous avons besoin d'une métrique fiable.

Un point de départ simple est le calcul des erreurs - les différences entre les valeurs prévues par notre modèle et les valeurs réelles sur la période d'évaluation. Cependant, nous avons besoin d'une manière plus standardisée de mesurer ces erreurs, et c'est là que plusieurs métriques couramment utilisées entrent en jeu.

Erreur quadratique moyenne (MSE)

Cette métrique consiste à mettre au carré les erreurs, puis à calculer leur moyenne. Le but de l'élévation au carré est d'éliminer les valeurs négatives, empêchant ainsi les erreurs de s'annuler mutuellement. Par exemple, si nous avons une erreur de +2 et une autre de -2, elles se compenseraient pour donner un total de zéro, laissant penser à tort qu'il n'y a pas d'erreur. Mais si nous mettons au carré ces erreurs, elles seront toutes deux élevées au carré pour donner 4, reflétant correctement la présence d'erreurs.

Erreur quadratique moyenne racine (RMSE)

En prenant la racine carrée de la MSE, le calcul de l'erreur revient à la même échelle que les erreurs originales, nous donnant le RMSE.

Erreur absolue moyenne (MAE)

Une autre métrique utile est l'Erreur Absolue Moyenne ou l'Écart Absolu Moyen. Au lieu de mettre au carré les erreurs, le MAE prend leurs valeurs absolues. Cela ne pénalise pas autant les grandes erreurs que le MSE. Selon les spécificités de votre tâche, vous pourriez préférer le MAE ou le MSE. Par exemple :

• Si de grandes erreurs sont potentiellement désastreuses et beaucoup plus coûteuses que les plus petites, vous pourriez pencher pour le MSE.
• Si vos gains ou pertes sont proportionnels à la taille de l'erreur, le MAE pourrait être un meilleur choix.

Erreur absolue moyenne en pourcentage (MAPE)

Le MAPE est le rapport moyen entre l'erreur absolue et la valeur absolue. Cette métrique donne une idée de la taille des erreurs par rapport aux valeurs.

Ces métriques peuvent être facilement calculées avec du code. Par exemple, la bibliothèque de métriques Keras inclut une fonction MAE. Avec les données synthétiques que nous avons présentées précédemment, nous obtenons un MAE d'environ 5,93.

Moyenne mobile et différenciation

Une méthode de prévision courante et simple est le calcul d'une moyenne mobile. Le concept consiste à tracer la moyenne des valeurs sur une période fixe, appelée fenêtre de moyenne. Cette approche réduit efficacement le bruit, fournissant une courbe qui émule approximativement la série originale. Cependant, elle n'anticipe ni la tendance ni la saisonnalité, ce qui peut la rendre moins précise que la prévision naïve dans certaines conditions.

Pour améliorer cela, nous pouvons utiliser une technique appelée différenciation. Au lieu d'examiner la série temporelle elle-même, nous examinons la différence entre la valeur au moment T et la valeur à une période antérieure. Cette période peut être un jour, un mois, une année ou toute autre période pertinente. Lorsqu'elle est appliquée à nos données, la différenciation élimine la tendance et la saisonnalité, produisant une nouvelle série temporelle de différences.

Après avoir obtenu cette série temporelle de différences, nous pouvons utiliser une moyenne mobile pour la prévoir. Mais souvenez-vous, ces prévisions sont pour la série temporelle de différences, pas la série originale. Pour obtenir les prévisions finales pour la série originale, nous ajoutons de nouveau la valeur au moment T de la période antérieure. Cette approche donne des prévisions considérablement améliorées.

Curieusement, nos prévisions de moyenne mobile sont toujours assez bruitées, même si elles ont éliminé une grande partie du bruit de la série originale. Ce bruit provient des valeurs passées que nous avons réintégrées dans nos prévisions. Nous pouvons atténuer cela en éliminant le bruit passé en utilisant également une moyenne mobile sur ces valeurs passées.

Lorsque nous mettons en œuvre cette étape finale, nous obtenons des prévisions beaucoup plus lisses et une erreur absolue moyenne considérablement réduite. Cette méthode étonnamment simple nous rapproche remarquablement de la performance d'un modèle parfait.

Ceci sert de rappel utile : avant de plonger tête baissée dans des modèles d'apprentissage profond complexes, envisagez de commencer par des méthodes plus simples. Parfois, elles fonctionnent très bien.

Bien que nous ayons examiné les moyennes mobiles en utilisant des fenêtres glissantes jusqu'à présent, il est important de noter que les moyennes mobiles utilisant des fenêtres centrées peuvent souvent être plus précises. Une fenêtre centrée prend en compte les valeurs avant et après un moment spécifique dans le temps. Cependant, l'utilisation de fenêtres centrées pour lisser les valeurs présentes n'est pas réalisable, car nous n'avons pas accès aux valeurs futures.

Néanmoins, en ce qui concerne le lissage des valeurs passées, nous pouvons exploiter la précision accrue des fenêtres centrées. Cela est dû au fait que nous avons accès aux valeurs futures nécessaires lors de l'examen des points passés dans le temps.

Après avoir exploré ces méthodes statistiques pour prédire les valeurs futures dans une série temporelle, il est essentiel de voir ces prédictions en pratique. C'est là que la mise en œuvre dans le monde réel et la pratique pratique entrent en jeu.

Prévisions

Nous commençons notre analyse avec l'ensemble de données synthétiques, où nous utiliserons des prévisions statistiques. Notre objectif est de générer une 'base', que nous chercherons ensuite à dépasser avec des algorithmes d'apprentissage automatique.

 import tensorflow as tf

# Assuming dataset is a DataFrame
dataset = tf.data.Dataset.from_tensor_slices(dataset.values)

Création d'une série temporelle avec tendance, saisonnalité et bruit

Ensuite, nous visons à créer une série temporelle qui inclut des tendances, de la saisonnalité et du bruit. Ces composantes représentent des aspects courants que l'on retrouve dans de nombreuses données de séries temporelles.

 # Assuming trend, seasonal_pattern, and noise_level are defined functions
time = tf.range(len(dataset))
baseline = trend(time, slope=0.1) 
seasonality = seasonal_pattern(time)
noise = noise_level(time)

series = baseline + seasonality + noise

Here, we first establish a timeline with the same length as our dataset. We then generate a baseline trend, a seasonal pattern, and noise, and combine them into our time series.

Training Validation Set Split

To assess our models effectively, we split our data into a training set and a validation set. Here, we cut the data array at the 1,000th index.

 train_data = series[:1000]
valid_data = series[1000:]

Cela nous fournit un ensemble d'entraînement des 1000 premières observations et un ensemble de validation pour toutes les données ultérieures.

Prédiction naïve

Notre première approche de prévision, la prévision naïve, suppose que la valeur future sera identique à la valeur actuelle. Nous calculons l'erreur quadratique moyenne (MSE) et l'erreur absolue moyenne (MAE) en tant que mesures pour évaluer la performance de cette prévision naïve.

 naive_forecast = series[1:]

mse = tf.keras.metrics.mean_squared_error(series[:-1], naive_forecast).numpy()
mae = tf.keras.metrics.mean_absolute_error(series[:-1], naive_forecast).numpy()

print('Mean Squared Error:', mse)
print('Mean Absolute Error:', mae)

Ici, nous créons une prévision naïve en décalant simplement la série d'une étape vers l'avenir. Ensuite, nous calculons le MSE et le MAE entre la série originale (à l'exception du dernier point) et la prévision naïve.

Moyenne mobile

Ensuite, nous explorons une autre approche courante de prévision, la moyenne mobile. Elle lisse la série en calculant la moyenne sur une fenêtre glissante de données.

 def moving_average(series, window_size):
  forecast = []
  for time in range(len(series) - window_size):
    forecast.append(series[time:time + window_size].numpy().mean())
  return np.array(forecast)

moving_avg = moving_average(series, 30)

Dans ce code, nous définissons une fonction pour calculer la moyenne mobile et l'appliquons à notre série. La taille de la fenêtre de 30 implique que nous calculons la moyenne sur les 30 points précédents pour chaque prévision.

Ajustement de la saisonnalité et amélioration de la moyenne mobile

En reconnaissant la saisonnalité de nos données (avec une période d'un an ou 365 jours), nous ajustons notre série en soustrayant la valeur de la série 365 jours plus tôt de la valeur actuelle de la série. Nous réappliquons ensuite notre moyenne mobile à cette série ajustée et ajoutons les valeurs passées pour obtenir une meilleure prédiction.

 diff_series = series[365:] - series[:-365]
diff_moving_avg = moving_average(diff_series, 50)

diff_moving_avg_plus_past = series[365:-50] + diff_moving_avg

mse = tf.keras.metrics.mean_squared_error(series[365:-50], diff_moving_avg_plus_past).numpy()
mae = tf.keras.metrics.mean_absolute_error(series[365:-50], diff_moving_avg_plus_past).numpy()

print('Mean Squared Error:', mse)
print('Mean Absolute Error:', mae)

Voici, nous créons d'abord la série_diff en soustrayant la valeur de la série de 365 jours précédents. Ensuite, nous calculons une moyenne mobile sur cette série_diff. En ajoutant ces moyennes mobiles aux points correspondants de la série passée, nous obtenons une prévision améliorée.

Apprentissage profond avec les séries temporelles

Pour tout problème d'apprentissage automatique, l'étape initiale consiste à diviser nos données en caractéristiques et étiquettes. Dans la prévision de séries temporelles, la caractéristique fait référence à un certain nombre de valeurs séquentielles dans notre ensemble de données, tandis que l'étiquette est la valeur suivante dans la série. Cet ensemble de valeurs séquentielles est également connu sous le nom de notre taille de fenêtre - un instantané de données que nous utilisons pour entraîner notre modèle d'apprentissage automatique à prédire la valeur suivante. À titre d'illustration, si nous travaillons avec des données de séries temporelles sur une période de 30 jours, nous utilisons les 30 valeurs comme caractéristiques et la valeur suivante comme étiquette. Par la suite, nous formons un réseau neuronal pour corréler les 30 caractéristiques avec l'étiquette unique.

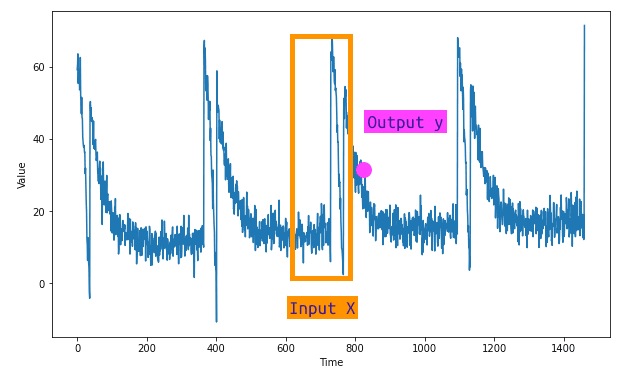
Nous utiliserons la classe tf.data.Dataset pour générer un ensemble de données, qui comprendra initialement une gamme de 10 valeurs. Lorsqu'il est visualisé, cette série de données s'étendra de 0 à 9.

 import tensorflow as tf

# Create a Dataset
dataset = tf.data.Dataset.range(10)

# Print each item in the dataset
for item in dataset:
    print(item.numpy())

result : 

0
1
2
3
4
5
6
7
8
9

Pour rendre les données plus complexes, nous utiliserons la méthode window de la classe Dataset pour agrandir notre ensemble de données. Cette méthode nécessite la taille de la fenêtre et le décalage comme paramètres. Par exemple, si nous choisissons une taille de fenêtre de 5 et un décalage de 1, la sortie sera une série de fenêtres, telles que 01234, 12345, et ainsi de suite. Lorsque nous atteignons la fin de l'ensemble de données, des fenêtres avec moins de 5 valeurs apparaîtront en raison d'un manque de données.

 import tensorflow as tf

# Create a Dataset
dataset = tf.data.Dataset.range(10)

# Apply the window method
dataset = dataset.window(5, shift=1)

# Print each window in the dataset
for window in dataset:
    for val in window:
        print(val.numpy(), end=" ")
    print()
    
result : 

0 1 2 3 4 
1 2 3 4 5 
2 3 4 5 6 
3 4 5 6 7 
4 5 6 7 8 
5 6 7 8 9 
6 7 8 9 
7 8 9 
8 9 
9 

Pour garantir une taille de fenêtre cohérente, nous pouvons ajuster la méthode window avec un paramètre supplémentaire - drop_remainder. En le définissant sur True, la méthode supprimera tous les restes, garantissant que toutes les fenêtres contiennent cinq éléments. Notre série commencera alors par 01234 et se terminera par 56789. Nous pouvons maintenant convertir ces fenêtres en tableaux numpy pour les préparer davantage aux opérations d'apprentissage automatique, ce qui peut être facilement accompli avec la méthode .numpy.

 import tensorflow as tf

# Create a Dataset
dataset = tf.data.Dataset.range(10)

# Apply the window method with drop_remainder
dataset = dataset.window(5, shift=1, drop_remainder=True)

# Batch the data and convert it to numpy arrays
dataset = dataset.flat_map(lambda window: window.batch(5))

# Print each window in the dataset
for window in dataset:
    print(window.numpy())
    
result : 

[0 1 2 3 4]
[1 2 3 4 5]
[2 3 4 5 6]
[3 4 5 6 7]
[4 5 6 7 8]
[5 6 7 8 9]

Ensuite, nous divisons les données en caractéristiques et étiquettes. Il est logique que toutes les valeurs sauf la dernière dans chaque fenêtre soient les caractéristiques, tandis que la dernière valeur est l'étiquette. Nous pouvons réaliser cela en utilisant la fonction mapping. Pour améliorer davantage notre ensemble de données, nous pouvons mélanger les données avant l'entraînement en utilisant la méthode shuffle.

 import tensorflow as tf

# Create a Dataset
dataset = tf.data.Dataset.range(10)

# Apply the window method with drop_remainder
dataset = dataset.window(5, shift=1, drop_remainder=True)

# Batch the data and convert it to numpy arrays
dataset = dataset.flat_map(lambda window: window.batch(5))

# Split the data into features and labels, and shuffle the data
dataset = dataset.map(lambda window: (window[:-1], window[-1:])).shuffle(buffer_size=10)

# Print each feature and label
for x, y in dataset:
    print("Feature: ", x.numpy(), "Label: ", y.numpy())
    
result

Feature:  [4 5 6 7] Label:  [8]
Feature:  [3 4 5 6] Label:  [7]
Feature:  [2 3 4 5] Label:  [6]
Feature:  [1 2 3 4] Label:  [5]
Feature:  [0 1 2 3] Label:  [4]
Feature:  [5 6 7 8] Label:  [9]

La dernière étape de la préparation des données consiste à regrouper les données en lots à l'aide de la méthode batch. Par exemple, en choisissant une taille de lot de 2, les données seront divisées en paires, créant ainsi trois lots au total. Chaque lot contient des paires de caractéristiques et d'étiquettes correspondantes.

Ensemble de données fenêtrées dans un réseau neuronal

Pour traiter des données de séries temporelles dans TensorFlow, nous pouvons créer une fonction appelée windowed_dataset. Cette fonction prendra trois arguments : série, taille de la fenêtre et taille de lot, ainsi qu'un paramètre supplémentaire shuffle_buffer qui facilitera le mélange des données. Voici comment nous pouvons définir la fonction :

 import tensorflow as tf

def windowed_dataset(series, window_size, batch_size, shuffle_buffer):
    # Step 1: Create a dataset from the series
    dataset = tf.data.Dataset.from_tensor_slices(series)
    
    # Step 2: Use the window method
    dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
    
    # Step 3: Flatten the data
    dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
    
    # Step 4: Shuffle the data
    dataset = dataset.shuffle(shuffle_buffer)
    
    # Step 5: Split into features and labels
    dataset = dataset.map(lambda window: (window[:-1], window[-1]))
    
    # Step 6: Batch the data
    dataset = dataset.batch(batch_size).prefetch(1)
    
    return dataset

Maintenant, décomposons cette fonction :

1. Créer un ensemble de données à partir de la série : La première étape consiste à créer un ensemble de données à partir des données de séries temporelles en utilisant la méthode tf.data.Dataset.from_tensor_slices de TensorFlow.

2. Fenêtrer les données : Ensuite, nous appliquons la méthode de fenêtrage à l'ensemble de données pour le diviser en fenêtres spécifiques, décalées chacune d'un pas de temps. Nous nous assurons que toutes les fenêtres ont la même taille en définissant drop_remainder sur True.

3. Aplatir les données : Pour faciliter le travail avec les données, nous les aplatissons en morceaux à l'aide de la méthode flat_map.

4. Mélanger les données : Les données sont ensuite mélangées à l'aide de la méthode shuffle. Le paramètre shuffle_buffer spécifie le nombre d'éléments du début de la séquence qui doivent être chargés, à partir desquels un élément sélectionné au hasard sera choisi.

5. Diviser en caractéristiques et étiquettes : Après le mélange, l'ensemble de données est divisé en caractéristiques (tous les éléments sauf le dernier de chaque fenêtre) et en étiquettes (le dernier élément de chaque fenêtre).

6. Mettre les données en lots : Enfin, les données sont regroupées en lots de la taille spécifiée batch_size, et la fonction renvoie cet ensemble de données final préparé.

Cette fonction vous permettra de créer une représentation gérable de vos données de séries temporelles, prête pour l'entraînement d'un modèle d'apprentissage automatique.

Réseau de neurones à une seule couche

Divisons maintenant nos données en ensembles d'entraînement et de validation. Ici, nous les divisons à l'instant 1000.

 # Assume series is our time-series data
split_time = 1000
x_train = series[:split_time]
x_valid = series[split_time:]

Maintenant nous pouvons créer et entrainer un simple modèle:

 import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD

# Set constants
window_size = 20
batch_size = 32
shuffle_buffer_size = 1000

# Create the windowed dataset
train_set = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)

# Define the model
l0 = Dense(1, input_shape=[window_size])  # A single dense layer
model = Sequential([l0])

# Compile the model
model.compile(loss="mse", optimizer=SGD(lr=1e-6, momentum=0.9))

# Train the model
model.fit(train_set, epochs=100, verbose=0)

# Print the weights
print("Layer weights: {}".format(l0.get_weights()))

Le modèle ne comporte qu'une seule couche, l0, qui est une couche dense avec un unique neurone. La couche est ajoutée au modèle en utilisant l'API Sequential. Le modèle est compilé avec l'erreur quadratique moyenne comme fonction de perte et la descente de gradient stochastique (SGD) comme optimiseur. Le taux d'apprentissage et le momentum pour SGD sont fixés à 1e-6 et 0.9, respectivement.

Ensuite, le modèle est entraîné sur l'ensemble d'entraînement train_set pendant 100 époques. Le paramètre verbose est réglé sur 0, donc aucune sortie d'entraînement n'est affichée.

Enfin, les poids de la couche l0 sont affichés. Le premier tableau représente les poids (20 valeurs dans ce cas, correspondant à la window_size), et la deuxième valeur est le biais. Ces valeurs sont apprises par le réseau pendant l'entraînement pour mieux ajuster les données. Les valeurs des poids et du biais représentent les paramètres du modèle de régression linéaire appris.

Prédiction

Plongeons dans la compréhension des subtilités de l'utilisation d'un réseau de neurones à une seule couche pour calculer la régression linéaire. Fondamentalement, les poids et le biais dans notre modèle sont utilisés pour faire des prédictions en fonction des données d'entrée. Par exemple, étant donné une série de 20 points de données, notre modèle de réseau neuronal est entraîné à utiliser ces valeurs d'entrée, à appliquer les poids, à ajouter le biais et à générer une sortie prédite.

Dans le contexte de TensorFlow, nous pouvons implémenter cela facilement. Voici un exemple simple :

 import tensorflow as tf
import numpy as np

# Assume x_values and y_values are your data points
x_values = np.random.rand(100)
y_values = x_values * 3 + 2 + np.random.randn(100)*0.1

# Define the model
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(1, input_shape=[1])
])

# Compile the model
model.compile(optimizer='sgd', loss='mean_squared_error')

# Fit the model
model.fit(x_values, y_values, epochs=10)

Dans cet exemple TensorFlow, un réseau de neurones à une seule couche est créé pour effectuer une régression linéaire. Nous entraînons le modèle sur nos valeurs x et y. Le modèle apprend à ajuster ses poids internes et son biais pour minimiser la différence entre les valeurs y réelles et prédites.

Après l'entraînement, si nous passons une série de 20 éléments de nos données à ce modèle, nous pouvons obtenir une prédiction :

 # Reshape your data
x_values_20 = x_values[:20].reshape(-1,1)

# Predict
predictions = model.predict(x_values_20)

Ici, le remodelage des données avec np.newaxis est nécessaire pour correspondre à la forme d'entrée requise par le modèle. Ensuite, model.predict génère une sortie prédite pour les 20 valeurs données.

Pour effectuer des prévisions, nous prenons les derniers éléments de taille window_size de la série, prédisons la prochaine valeur et l'ajoutons à la série. Nous répétons ce processus pour générer autant de prévisions que nécessaire :

 forecasts = []
for time in range(len(series) - window_size):
    forecast = model.predict(series[time:time + window_size][np.newaxis])
    forecasts.append(forecast)

forecasts = forecasts[split_time-window_size:]
results = np.array(forecasts)[:, 0, 0]

Nous pouvons créer un graphique pour comparer les valeurs réelles aux valeurs prédites :

 import matplotlib.pyplot as plt

plt.figure(figsize=(10,6))
plt.plot(x_values, y_values, 'b.')
plt.plot(x_values[:20], predictions, 'r-')
plt.show()

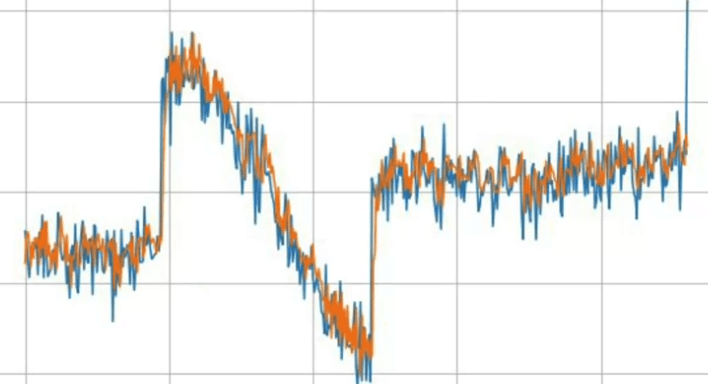
Les points bleus représentent les valeurs réelles et la ligne rouge représente les prédictions de notre modèle.

Nous pouvons également calculer l'erreur absolue moyenne (MAE) pour évaluer la qualité de nos prédictions :

 mae = tf.keras.losses.mean_absolute_error(y_values[:20], predictions)
print('Mean Absolute Error:', mae.numpy())

Améliorer les prédictions

Pour continuer là où nous nous sommes arrêtés, nous pouvons exploiter la puissance d'un réseau de neurones profonds (DNN) pour améliorer davantage la précision de notre modèle. Cet exemple décrit l'application d'un DNN à trois couches simple pour effectuer des prévisions de séries temporelles plus précises.

Tout d'abord, nous devons générer notre ensemble de données. Nous utilisons la fonction windowed_dataset précédemment définie et passons nos données d'entraînement (x_train), la taille de fenêtre souhaitée, la taille du lot (batch size) et la taille du tampon de mélange (shuffle buffer size).

 dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)

Le modèle est défini comme un DNN à trois couches avec 10 neurones dans chacune des deux premières couches et 1 neurone dans la dernière couche. La forme d'entrée correspond à la taille de la fenêtre, et nous utilisons ReLU (Rectified Linear Unit) comme fonction d'activation dans chaque couche.

 model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(10, activation="relu", input_shape=[window_size]),
    tf.keras.layers.Dense(10, activation="relu"),
    tf.keras.layers.Dense(1)
])

Ensuite, nous compilons le modèle avec une fonction de perte Mean Squared Error (MSE) et la descente de gradient stochastique (SGD) comme optimiseur.

 model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD())

Nous ajustons le modèle sur 100 époques, puis calculons l'erreur absolue moyenne (MAE). Si nous constatons que le MAE a diminué, cela indique que nous avons amélioré les capacités de prédiction de notre modèle.

Une manière de mieux améliorer l'efficacité d'apprentissage et de construire un meilleur modèle est de trouver un taux d'apprentissage optimal. Pour cela, nous introduisons un planificateur de taux d'apprentissage en tant que fonction de rappel (callback). Cette fonction ajuste le taux d'apprentissage à la fin de chaque époque en fonction du numéro d'époque.

 lr_schedule = tf.keras.callbacks.LearningRateScheduler(
    lambda epoch: 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss="mse", optimizer=optimizer)
history = model.fit(dataset, epochs=100, callbacks=[lr_schedule])

Nous pouvons tracer la perte par époque par rapport au taux d'apprentissage par époque pour trouver le taux d'apprentissage optimal, qui correspond au taux offrant la perte la plus faible et stable.

 lrs = 1e-8 * (10 ** (np.arange(100) / 20))
plt.semilogx(lrs, history.history["loss"])
plt.axis([1e-8, 1e-3, 0, 300])

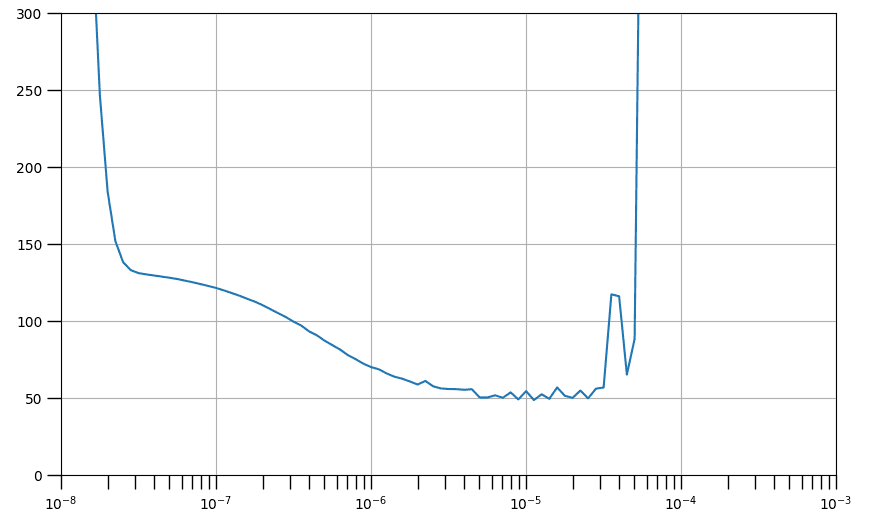
Le graphique présenté ci-dessus illustre l'assortiment de taux d'apprentissage qui contribuent à une diminution des pertes, comme indiqué par une tendance à la baisse, et ceux qui précipitent l'instabilité du processus d'entraînement, ce qui est représenté par des bords irréguliers et une trajectoire ascendante. En général, un point sur une pente descendante est optimal pour la sélection, car il suggère que le réseau continue d'apprendre tout en maintenant la stabilité. Choisir un point près du minimum du graphique accélérera la convergence de l'entraînement vers cette valeur de perte spécifique, comme le démontreront les cellules suivantes.

Nous allons maintenant procéder à l'initialisation de la même architecture de modèle qu'auparavant. Vous allez établir l'optimiseur avec un taux d'apprentissage approximatif du minimum. Il est initialement réglé à 4e-6, mais vous êtes libre de l'ajuster en fonction de vos résultats.

 # Build the model
model_tune = tf.keras.models.Sequential([
  tf.keras.layers.Dense(10, activation="relu", input_shape=[window_size]),
  tf.keras.layers.Dense(10, activation="relu"),
  tf.keras.layers.Dense(1)
])

# Set the optimizer with the tuned learning rate
optimizer = tf.keras.optimizers.SGD(learning_rate=4e-6, momentum=0.9)

Ensuite, compilez et entraînez le modèle comme précédemment. Prêtez une attention particulière aux valeurs de perte et comparez-les à la sortie de votre modèle de référence précédent. Il est fort probable que la valeur de perte finale de model_baseline soit atteinte au cours des 50 premières époques de l'entraînement de ce model_tune. Après avoir terminé les 100 époques, il est également probable que vous observiez une perte réduite.

 # Set the training parameters
model_tune.compile(loss="mse", optimizer=optimizer)

# Train the model
history = model_tune.fit(dataset, epochs=100)

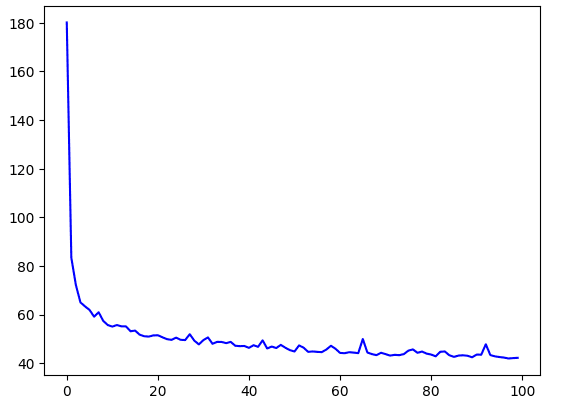
Résultat :

 # Plot the loss
loss = history.history['loss']
epochs = range(len(loss))
plt.plot(epochs, loss, 'b', label='Training Loss')
plt.show()

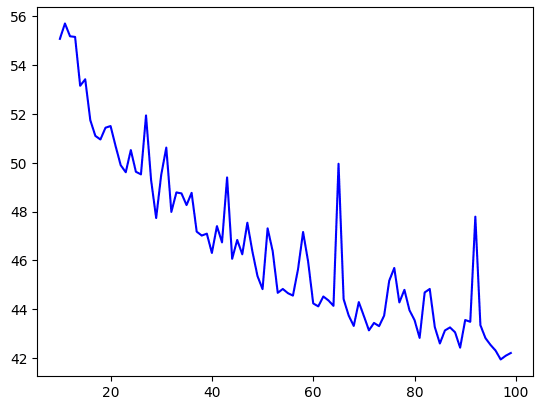
 # Plot all but the first 10
loss = history.history['loss']
epochs = range(10, len(loss))
plot_loss = loss[10:]
plt.plot(epochs, plot_loss, 'b', label='Training Loss')
plt.show()

Vous pouvez obtenir à nouveau les prédictions et les superposer à l'ensemble de validation.

 # Initialize a list
forecast = []

# Reduce the original series
forecast_series = series[split_time - window_size:]

# Use the model to predict data points per window size
for time in range(len(forecast_series) - window_size):
  forecast.append(model_tune.predict(forecast_series[time:time + window_size][np.newaxis]))

# Convert to a numpy array and drop single dimensional axes
results = np.array(forecast).squeeze()

# Plot the results
plot_series(time_valid, (x_valid, results))

Enfin, calculez les métriques ; vous devriez obtenir des chiffres comparables à ceux de la référence. Si les résultats sont nettement pires, le modèle pourrait être surajusté. Dans ce cas, vous pouvez mettre en œuvre des techniques pour l'éviter, telles que l'introduction de la désactivation (dropout).

 print(tf.keras.metrics.mean_squared_error(x_valid, results).numpy())
print(tf.keras.metrics.mean_absolute_error(x_valid, results).numpy())

Réseaux de neurones récurrents

Les réseaux de neurones récurrents (RNN) sont un type puissant d'architecture de réseau neuronal conçu pour traiter des données séquentielles. Au cœur d'un RNN se trouve la couche récurrente, qui permet au réseau de conserver des informations sur les entrées précédentes tout en traitant de nouvelles entrées. Cette capacité unique rend les RNN bien adaptés à la manipulation de séquences de données, telles que les séries temporelles. Contrairement à d'autres réseaux neuronaux, les RNN prennent en compte l'aspect temporel des données, en tenant compte de l'ordre et de la relation entre différentes étapes temporelles.

Architecture

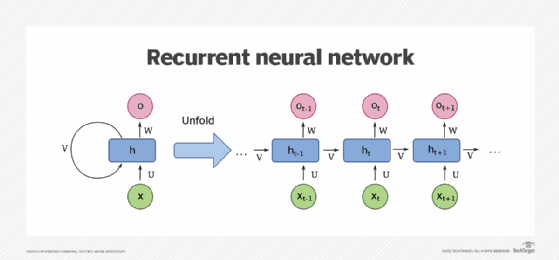
Un RNN est composé d'une ou plusieurs couches récurrentes. Chaque couche contient une cellule mémoire, qui est responsable de stocker des informations sur les entrées passées. Bien qu'il puisse sembler qu'il y ait plusieurs cellules, en réalité, il n'y a qu'une seule cellule qui est réutilisée à chaque étape temporelle. Cette cellule prend une valeur d'entrée pour l'étape temporelle actuelle et produit une sortie ainsi qu'un vecteur d'état. Le vecteur d'état est ensuite réinjecté dans la cellule à l'étape suivante, créant ainsi une boucle récurrente qui permet aux informations de circuler à travers le réseau.

Application des RNN à l'analyse de séries temporelles

Dans le contexte de l'analyse de séries temporelles, un RNN peut être utilisé pour prévoir les valeurs futures en fonction des observations historiques. En formant le réseau sur des données passées, il apprend à capturer les motifs et les dépendances présents dans la série temporelle. Pour les séries temporelles univariées, où seule une variable est considérée, la dimension d'entrée est de un. Cependant, pour les séries temporelles multivariées, avec plusieurs variables influençant la prédiction, la dimension d'entrée augmente en conséquence.

La nature récurrente des RNN est particulièrement bénéfique pour capturer les dépendances temporelles au sein d'une série temporelle. De la même manière que la position d'un mot dans une phrase peut influencer sa signification dans le traitement du langage naturel, la proximité des valeurs dans une série numérique peut également avoir un impact significatif sur les prédictions. Les RNN excellent dans la capture de ces relations, ce qui leur permet de faire des prédictions informées en fonction de la nature séquentielle des données.

Entrées tridimensionnelles

Lorsque l'on travaille avec des RNN, les entrées sont représentées sous une forme tridimensionnelle. Pour illustrer cela, considérons un exemple où nous avons une taille de fenêtre de 30 horodatages, et nous les regroupons par lots de quatre. Dans ce cas, la forme des données d'entrée serait de 4x30x1. L'entrée de chaque horodatage vers la cellule mémoire serait une matrice 4x1, indiquant une taille de lot de quatre et une seule dimension pour chaque étape temporelle.

La cellule mémoire dans un RNN prend à la fois l'entrée actuelle et la matrice d'état de sortie précédente comme entrées. Cependant, à la première étape temporelle, la matrice d'état précédente serait initialisée à zéro. Aux étapes suivantes, elle serait la sortie de la cellule mémoire de l'étape temporelle précédente.

La cellule mémoire produit à la fois une valeur Y et un vecteur d'état. Supposons que la cellule mémoire comporte trois neurones. La matrice de sortie serait alors de 4x3 car la taille du lot est de quatre et le nombre de neurones est de trois. En conséquence, la sortie complète de la couche serait tridimensionnelle, dans cet exemple 4x30x3. Ici, quatre représente la taille du lot, trois représente le nombre de neurones et trente signifie le nombre d'étapes au total.

La sortie d'état H est simplement une copie de la matrice de sortie Y. Par exemple, H_0 est une copie de Y_0, H_1 est une copie de Y_1, et ainsi de suite. À chaque horodatage, la cellule mémoire reçoit à la fois l'entrée actuelle et la sortie précédente pour effectuer des calculs.

Dans certains cas, vous n'aurez peut-être besoin que d'une seule sortie de vecteur pour chaque instance dans le lot, même si vous entrez une séquence de données. Cela est couramment appelé un RNN de séquence à vecteur. En pratique, il suffit d'ignorer toutes les sorties sauf la dernière. Lorsque vous utilisez des frameworks comme Keras dans TensorFlow, ce comportement est le paramètre par défaut. Si vous souhaitez que la couche récurrente produise une séquence de sortie à la place, vous devez spécifier explicitement return_sequences=True lors de la création de la couche. Cela devient nécessaire lorsque vous empilez une couche RNN sur une autre pour propager des informations séquentielles dans tout le réseau.

TensorFlow

 # Build the Model
model_tune = tf.keras.models.Sequential([
  tf.keras.layers.SimpleRNN(20, return_sequences=True),
  tf.keras.layers.SimpleRNN(20, return_sequences=True),
  tf.keras.layers.Dense(1),
])

# Print the model summary
model_tune.summary()

La première couche de notre RNN exemplaire a return_sequences=True, ce qui lui permet de générer une séquence. Cette sortie sert ensuite de terrain d'alimentation pour la couche suivante. Cependant, la couche suivante n'a pas return_sequences défini comme True, ce qui fait qu'elle produit une sortie à la dernière étape uniquement.

En prêtant attention au paramètre input_shape, nous observons qu'il est défini comme None et 1. Dans le monde de TensorFlow, la première dimension représente la taille du lot (batch size). La partie intrigante ici est que TensorFlow n'est pas pointilleux sur la taille et vous pouvez laisser cette dimension indéfinie. La dimension suivante symbolise le nombre d'horodatages (timestamps). En laissant cela à None, l'RNN est capable de manipuler des séquences de longueurs différentes. La dernière dimension est un singleton, reflétant la nature univariée de notre série temporelle.

Maintenant, si nous choisissons de définir return_sequences comme True pour toutes les couches récurrentes, un changement intéressant se produit. Elles commencent toutes à produire des séquences et, par conséquent, la couche dense reçoit une séquence en tant qu'entrée. Keras gère ce comportement en utilisant la même couche dense indépendamment à chaque horodatage. Cela peut donner l'illusion de plusieurs couches, mais c'est la même couche, réutilisée à chaque étape temporelle. Cet agencement intrigant donne naissance à un RNN de séquence à séquence, qui ingère un lot de séquences et renvoie un lot de séquences de même longueur.

 # Build the Model
model_tune = tf.keras.models.Sequential([
  tf.keras.layers.SimpleRNN(20, return_sequences=True),
  tf.keras.layers.SimpleRNN(20),
  tf.keras.layers.Dense(1),
])

# Print the model summary
model_tune.summary()

Cependant, les dimensions pourraient ne pas toujours correspondre parfaitement. Cela dépend du nombre d'unités résidant dans la cellule de mémoire.

Type Lambda

Les RNN sont en effet polyvalents, mais parfois nous devons ajouter une touche de personnalisation pour mieux adapter nos tâches. C'est là que les couches Lambda entrent en jeu, nous donnant la liberté d'effectuer des opérations arbitraires à l'intérieur de la définition du modèle lui-même, enrichissant ainsi les capacités de TensorFlow's Keras.

Tout d'abord, abordons la disparité dans les dimensions. Notre fonction d'aide de jeu de données de fenêtre renvoie des lots bidimensionnels de fenêtres - un pour la taille du lot et l'autre pour le nombre de points temporels. Cependant, un RNN nécessite trois dimensions - la taille du lot, le nombre de points temporels et la dimensionnalité de la série. C'est là que nous pouvons utiliser une couche Lambda pour ajouter une dimension supplémentaire sans avoir à modifier notre fonction d'aide de jeu de données de fenêtre. En définissant la forme d'entrée comme nulle, nous exprimons que le modèle peut consommer des séquences de n'importe quelle longueur.

Deuxièmement, nous traiterons l'échelle de nos sorties pour aider à l'apprentissage. Les couches RNN, par défaut, utilisent la fonction d'activation tangente hyperbolique (tanh), qui restreint les valeurs de sortie entre -1 et 1. Comme nos valeurs de séries chronologiques se situent généralement dans les dizaines (par exemple, années 40, 50, 60 et 70), la rééchelle de nos sorties pour correspondre à cette plage peut améliorer l'apprentissage. Une couche Lambda fournit la toile parfaite pour accomplir cela ; nous multiplions simplement la sortie par 100.

 import tensorflow as tf
from tensorflow.keras import layers

model = tf.keras.models.Sequential([
    layers.Lambda(lambda x: tf.expand_dims(x, axis=-1), input_shape=[None]),
    layers.SimpleRNN(20, return_sequences=True),
    layers.SimpleRNN(20),
    layers.Dense(1),
    layers.Lambda(lambda x: x * 100.0)
])

model.compile(optimizer='adam', loss='mse')

# Now your model is ready to be trained with your data

Ajustement des taux d'apprentissage

Les réseaux de neurones récurrents (RNN) peuvent être assez efficaces pour les prédictions de séries temporelles. Pour améliorer l'efficacité de l'entraînement de notre modèle et les performances de prédiction, nous allons également ajuster le taux d'apprentissage de notre optimiseur de réseau neuronal. Cette approche stratégique peut permettre de gagner un temps considérable lors de l'ajustement des hyperparamètres.

Nous allons entraîner un RNN avec deux couches, chacune comportant 40 cellules. Pour affiner le taux d'apprentissage, nous allons utiliser une rappel qui ajuste légèrement le taux d'apprentissage à la fin de chaque époque. De plus, nous allons utiliser une nouvelle fonction de perte, la « perte de Huber ». Cette fonction est particulièrement utile lorsque l'on traite des données bruyantes car elle est moins sensible aux valeurs aberrantes.

 # Define learning rate schedule
def lr_schedule(epoch):
    return 10 ** (epoch / 20)

lr_callback = LearningRateScheduler(lr_schedule)

model = tf.keras.models.Sequential([
    layers.Lambda(lambda x: tf.expand_dims(x, axis=-1), input_shape=[None]),
    layers.SimpleRNN(40, return_sequences=True),
    layers.SimpleRNN(40),
    layers.Dense(1),
    layers.Lambda(lambda x: x * 100.0)
])

optimizer = SGD(lr=1e-8, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=optimizer, metrics=["mae"])

history = model.fit(dataset, epochs=100, callbacks=[lr_callback])

Après 100 époques d'entraînement, nous pouvons déterminer notre taux d'apprentissage optimal pour la descente de gradient stochastique (SGD) quelque part entre 10^-5 et 10^-6. Nous allons maintenant entraîner notre modèle pendant 500 époques en utilisant ce taux d'apprentissage et l'optimiseur SGD.

Après l'entraînement, le graphique présentant l'erreur absolue moyenne (MAE) sur l'ensemble de validation montre une MAE d'environ 6,35. Bien que ce ne soit pas mal, nous devrions viser à faire mieux.

En regardant de plus près, nous constatons que la tendance à la diminution de la perte se poursuit jusqu'à environ 400 époques, après quoi elle commence à fluctuer. Compte tenu de cela, un entraînement d'environ 400 époques devrait être suffisant.

Voici comment nous re-entraînons notre modèle avec ces paramètres :

 optimizer = SGD(lr=1e-5, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=optimizer, metrics=["mae"])
history = model.fit(dataset, epochs=400)

Nous remarquons que la MAE est légèrement plus élevée, mais les économies de temps provenant de 100 époques d'entraînement en moins en font un compromis équitable. L'évaluation de la MAE et de la perte d'entraînement montre des résultats prometteurs. Ainsi, même un modèle RNN simple peut offrir des performances remarquables.

LSTM

Bien que nos résultats avec le modèle RNN simple étaient corrects, il y avait des plateaux singuliers dans les prédictions qui indiquent des possibilités d'amélioration. Malgré l'expérimentation avec divers hyperparamètres, l'amélioration était modeste. Maintenant, passons à autre chose et explorons le potentiel des réseaux Long Short-Term Memory (LSTM) en tant qu'alternative aux RNN.

Rappelez-vous notre discussion sur les RNN : ils se composent de cellules qui traitent les entrées par lots (X) et génèrent une sortie (Y) ainsi qu'un vecteur d'état. Ce vecteur d'état, avec la prochaine entrée, est transmis à la cellule suivante, où il contribue au calcul de la prochaine sortie et du prochain vecteur d'état. Cependant, l'influence du vecteur d'état peut diminuer au fil des horodatages, ce qui pourrait être un inconvénient potentiel, en particulier pour les séquences longues.

Les LSTM abordent cette influence décroissante en introduisant un « état de cellule » qui persiste tout au long du processus d'entraînement. Cet état est transmis de cellule en cellule et d'horodatage en horodatage, garantissant une meilleure rétention de la « mémoire » des données passées. Par conséquent, les données des parties antérieures de la séquence peuvent avoir un impact plus important sur la prédiction globale par rapport au cas des RNN simples.

Fait intéressant, les LSTM peuvent également exploiter des états bidirectionnels, où l'information circule à la fois en avant et en arrière. Cette approche s'est révélée incroyablement bénéfique pour l'analyse de texte. En ce qui concerne la prédiction de séquences numériques, l'avantage des états bidirectionnels n'est pas aussi clair, ce qui en fait un domaine intrigant pour l'expérimentation.

Passer des RNN aux LSTM nécessite quelques ajustements à notre code existant. Décortiquons les changements :

 import tensorflow as tf
from tensorflow.keras import layers

tf.keras.backend.clear_session()

model = tf.keras.models.Sequential([
    layers.Lambda(lambda x: tf.expand_dims(x, axis=-1), input_shape=[None]),
    layers.Bidirectional(layers.LSTM(32, return_sequences=False)),
    layers.Dense(1),
    layers.Lambda(lambda x: x * 100.0)
])

optimizer = tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=optimizer, metrics=["mae"])

Initialement, tf.keras.backend.clear_session() est utilisé pour effacer toutes les variables internes, garantissant que nos itérations n'interfèrent pas les unes avec les autres. Après notre couche Lambda d'expansion de dimensions, nous introduisons une couche LSTM bidirectionnelle avec 32 cellules. Le neurone de sortie génère ensuite notre valeur de prédiction. Le taux d'apprentissage est fixé à 1e-6, ce qui est sujet à des expérimentations ultérieures.

Après avoir exécuté ce modèle LSTM sur nos données synthétiques, les résultats montrent toujours un plateau sous le pic majeur, et la MAE est modérément basse. Les prédictions pourraient également être légèrement sous-estimées.

Pour améliorer cela, nous ajoutons une autre couche LSTM à notre modèle :

 model = tf.keras.models.Sequential([
    layers.Lambda(lambda x: tf.expand_dims(x, axis=-1), input_shape=[None]),
    layers.Bidirectional(layers.LSTM(32, return_sequences=True)),
    layers.Bidirectional(layers.LSTM(32, return_sequences=False)),
    layers.Dense(1),
    layers.Lambda(lambda x: x * 100.0)
])

Nous devons définir return_sequences=True dans la première couche LSTM pour que la deuxième couche LSTM fonctionne correctement. Les résultats montrent maintenant un suivi beaucoup plus précis des données d'origine, bien qu'il puisse légèrement prendre du retard lors de fortes augmentations. La MAE s'est également nettement améliorée.

Ensuite, nous ajoutons une troisième couche LSTM :

 model = tf.keras.models.Sequential([
    layers.Lambda(lambda x: tf.expand_dims(x, axis=-1), input_shape=[None]),
    layers.Bidirectional(layers.LSTM(32, return_sequences=True)),
    layers.Bidirectional(layers.LSTM(32, return_sequences=True)),
    layers.Bidirectional(layers.LSTM(32, return_sequences=False)),
    layers.Dense(1),
    layers.Lambda(lambda x: x * 100.0)
])

After training and running this updated model, we can compare the outputs and evaluate the benefits of having three LSTM layers.