Apprentissage par renforcement

Introduction

Dans cet article, nous allons explorer l'apprentissage par renforcement, qui est un concept fondamental dans le domaine de l'apprentissage automatique. Bien qu'il ne soit pas encore largement utilisé dans les applications commerciales, il a un immense potentiel et est soutenu par une recherche approfondie qui améliore constamment ses capacités. Pour illustrer ce concept, commençons par prendre l'exemple d'un hélicoptère autonome, équipé d'un ordinateur embarqué, d'un GPS, d'accéléromètres, de gyroscopes et d'une boussole magnétique. La tâche est d'écrire un programme qui permet à l'hélicoptère de voler de manière autonome en utilisant un algorithme d'apprentissage par renforcement.

Pour y parvenir, nous devons d'abord comprendre les concepts d'"état" et d'"action". Dans l'apprentissage par renforcement, "l'état" du système fait référence à la position, à l'orientation, à la vitesse et à d'autres informations pertinentes sur l'hélicoptère. D'autre part, "l'action" fait référence à la réponse du système à l'état actuel. Dans le cas de l'hélicoptère, il s'agit de savoir dans quelle mesure pousser les deux manettes de commande pour le maintenir en équilibre dans les airs et l'empêcher de s'écraser.

Une approche pour résoudre ce problème est d'utiliser l'apprentissage supervisé, où un réseau de neurones peut être entraîné à l'aide d'un ensemble de données d'états et de l'action optimale correspondante, fournie par un pilote humain expert. Cependant, cette méthode n'est pas idéale pour le vol d'hélicoptère autonome, car il est difficile d'obtenir un grand ensemble de données de l'action optimale exacte pour chaque état. Au lieu de cela, l'apprentissage par renforcement est utilisé, ce qui offre plus de flexibilité dans la conception et la formation du système.

Dans l'apprentissage par renforcement, une "fonction de récompense" est utilisée pour former le système. Tout comme on entraînerait un chien en le louant lorsqu'il se comporte bien et en le corrigeant lorsqu'il se comporte mal, une fonction de récompense est utilisée pour inciter le système à bien se comporter. Dans le cas de l'hélicoptère, une récompense de plus un peut être donnée chaque seconde où il vole bien, tandis qu'une récompense négative est donnée pour un mauvais vol, et une grande récompense négative pour un crash.

L'apprentissage par renforcement est un concept puissant car il nous permet de dire au système quoi faire plutôt que comment le faire. Cela signifie que nous pouvons spécifier la fonction de récompense et laisser l'algorithme déterminer automatiquement comment choisir l'action optimale en réponse à l'état actuel. Cette approche a été appliquée avec succès à diverses applications, telles que le contrôle de robots, l'optimisation de l'usine, le commerce des actions financières et les jeux.

Le rover de Mars

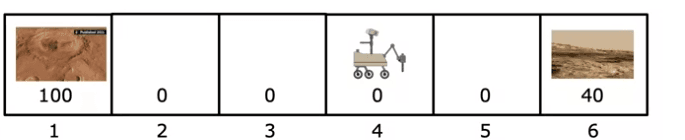
Pour illustrer le concept de l'apprentissage par renforcement, nous utiliserons un exemple simplifié inspiré du rover de Mars. L'exemple consiste en un rover qui peut se trouver dans l'une des six positions, que nous appellerons état 1 à état 6.

États et récompenses:

Chaque état a une valeur différente, représentée par une fonction de récompense. L'état 1 est le plus précieux, avec une récompense de 100, et l'état 6 est moins précieux, avec une récompense de 40. Les récompenses pour tous les autres états sont nulles car il n'y a pas autant de science intéressante à faire.

Actions du robot:

À chaque étape, le rover peut choisir de se déplacer vers la gauche ou la droite depuis sa position actuelle. Le rover peut choisir l'une des deux actions : il peut soit aller vers la gauche, soit aller vers la droite.

Objectifs du robot:

L'objectif de l'algorithme d'apprentissage par renforcement est de maximiser la récompense que le rover reçoit. En d'autres termes, le rover doit apprendre comment choisir les actions qui mèneront aux états les plus précieux.

États et transitions du robot:

La position du rover de Mars est appelée l'état dans l'apprentissage par renforcement. Le rover peut se trouver dans l'un des six états, et le rover commence en état 4. L'état dans lequel le rover se trouve déterminera les récompenses que le rover reçoit lorsqu'il prend certaines actions.

Décisions du robot:

Le rover peut prendre des décisions sur la direction à prendre en fonction des récompenses associées à chaque état. Par exemple, l'état 1 à gauche a une surface très intéressante que les scientifiques aimeraient que le rover échantillonne. L'état 6 a également une surface assez intéressante que les scientifiques aimeraient que le rover échantillonne, mais pas autant que l'état 1.

Apprentissage du robot:

Les algorithmes d'apprentissage par renforcement utilisent l'état, l'action, la récompense et l'état suivant pour décider quelles actions prendre dans chaque état, dans le but de maximiser la récompense totale obtenue au fil du temps. En appliquant ce concept à des tâches plus complexes, telles que le contrôle d'un hélicoptère ou d'un robot chien, nous pouvons créer des machines intelligentes capables d'apprendre de leur environnement et d'accomplir des tâches de plus en plus complexes.

En résumé, l'exemple du rover de Mars fournit un exemple simplifié mais illustratif des concepts de l'apprentissage par renforcement. En enseignant aux machines à prendre des décisions basées sur des récompenses et des états, nous pouvons créer des machines intelligentes capables d'apprendre de leur environnement et d'accomplir des tâches complexes.

Le retour de l'apprentissage par renforcement

L'apprentissage par renforcement consiste à prendre des actions qui conduisent à différents états et récompenses. Mais comment déterminer quel ensemble de récompenses est meilleur qu'un autre ? C'est là que le concept de retour entre en jeu, qui capture la valeur des récompenses en fonction de leur moment. Dans cet section, nous explorerons l'idée de retour et son application dans l'apprentissage par renforcement.

L'importance du retour

Lorsque nous prenons des actions dans un système d'apprentissage par renforcement, les récompenses reçues peuvent varier considérablement. Cependant, nous devons déterminer quel ensemble de récompenses est plus précieux. C'est là que le concept de retour entre en jeu, car il nous aide à capturer la valeur des récompenses au fil du temps.

Pour illustrer ce concept, imaginons que nous avons un billet de cinq dollars à nos pieds et un billet de dix dollars à une demi-heure de marche dans une ville voisine. Bien que dix dollars soit mieux que cinq dollars, cela peut ne pas valoir la peine de marcher une demi-heure pour l'obtenir. Le retour nous aide à déterminer la valeur des récompenses qui peuvent être obtenues plus rapidement par rapport à celles qui prennent plus de temps à réaliser.

Comprendre la formule de retour

Le retour est la somme des récompenses, pondérées par le facteur de remise. Ce facteur de remise est un nombre légèrement inférieur à un, et il détermine la valeur des récompenses reçues à différents moments. Une valeur de facteur de remise courante est 0,9, mais elle peut varier de 0 à 1.

Par exemple, considérons un exemple de Rover de Mars où nous commençons à l'état 4 et nous déplaçons vers la gauche. Les récompenses que nous recevons sont 0, 0, 0 et 100 à l'état terminal. Si nous fixons le facteur de remise à 0,9, nous pouvons calculer le retour comme suit :

Retour = 0 + 0,9 * 0 + 0,9^2 * 0 + 0,9^3 * 100 = 72,9

La formule plus générale pour calculer le retour est:

R_1 + Gamma * R_2 + Gamma^2 * R_3 + ... + Gamma^n * R_n

où R_n est la récompense à l'étape n et Gamma est le facteur de remise.

L'impact du facteur de remise

Le facteur de remise a un impact sur la valeur du retour. L'algorithme d'apprentissage par renforcement devient plus impatient avec un facteur de remise plus élevé, car les récompenses reçues plus tôt sont données plus de poids dans le calcul du retour. Un choix courant pour le facteur de remise est 0,9 ou 0,99, mais cela peut varier en fonction de l'application.

Nous pouvons également définir le facteur de remise à une valeur plus proche de 0, comme 0,5, ce qui réduit considérablement les récompenses futures. Dans les applications financières, le facteur de remise peut représenter la valeur temporelle de l'argent ou les taux d'intérêt.

Calculer les retours pour différents états et actions

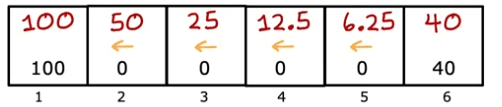
Le retour dépend des récompenses reçues, qui dépendent à leur tour des actions prises. En prenant différentes actions dans différents états, nous pouvons obtenir différents retours. Par exemple, si nous allons toujours à gauche, le retour pour l'état 4 est de 12,5, mais si nous allons toujours à droite, il est de 10.

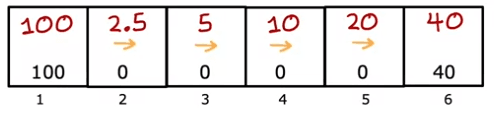
Nous pouvons également choisir des actions en fonction de l'état dans lequel nous nous trouvons, comme aller à gauche dans les états 2 et 3 mais aller à droite dans l'état 5. Cela donne des retours différents pour chaque état, l'état 1 ayant un retour de 100, l'état 2 ayant un retour de 50, etc.

Récompenses négatives et facteur de remise

Dans les systèmes avec des récompenses négatives, le facteur de remise incite le système à repousser les récompenses négatives aussi loin que possible dans le futur. C'est parce que les récompenses négatives futures sont plus fortement réduites que les récompenses négatives dans le présent. Cela peut être bénéfique dans les applications financières où il est préférable de différer les paiements en raison des taux d'intérêt.

Prendre des décisions

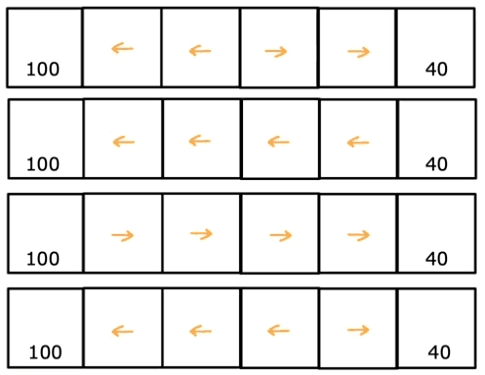
L'objectif est de trouver une politique, notée Pi, qui mappe l'état actuel de l'agent à une action qui maximise la récompense attendue.

Il existe de nombreuses façons de choisir des actions en apprentissage par renforcement, telles que toujours aller chercher la récompense la plus proche ou toujours aller chercher la plus grande récompense. Pour trouver la politique optimale, nous devons prendre en compte l'état actuel de l'agent, les actions qu'il peut prendre et les récompenses associées à ces actions.

Le retour est un concept important en apprentissage par renforcement, qui fait référence à la somme des récompenses que l'agent reçoit, pondérée par un facteur de remise. Ce facteur incite l'agent à privilégier les récompenses qui sont plus proches dans le temps, car elles sont pondérées plus lourdement que les récompenses qui sont plus éloignées.

Une fonction de politique Pi est utilisée pour mapper les états aux actions, et l'objectif de l'apprentissage par renforcement est de trouver la politique optimale qui maximise le retour. Pour y parvenir, divers algorithmes peuvent être utilisés pour mettre à jour de manière itérative la politique en fonction des expériences de l'agent dans l'environnement.

Décision markovien

Le problème est formulé comme un processus de décision markovien, ou MDP pour faire court, qui comprend des états, des actions, des récompenses et un facteur de remise. L'objectif de l'agent est de trouver une politique qui mappe les états aux actions afin de maximiser le retour attendu, qui est calculé à l'aide des récompenses et du facteur de remise.

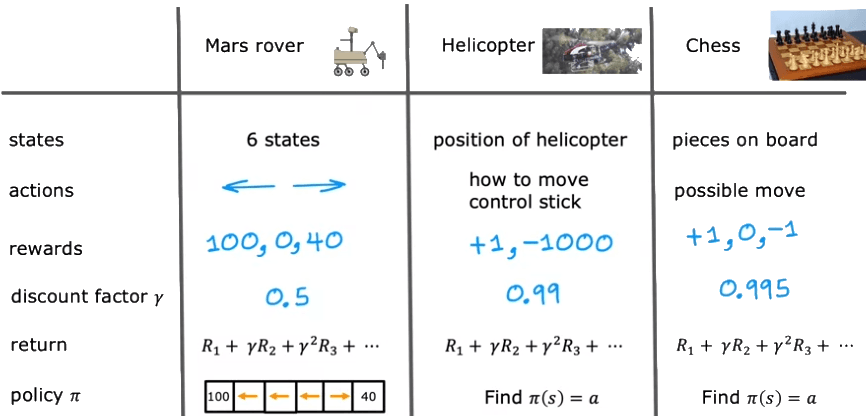
Par exemple, dans le cas d'un rover sur Mars : Les états sont les six positions possibles, les actions sont les mouvements vers la gauche ou la droite, et les récompenses sont de 100 pour l'état le plus à gauche, 40 pour l'état le plus à droite, et zéro entre les deux, avec un facteur de remise de 0,5.

Un autre exemple est le contrôle d'un hélicoptère autonome, où les états sont les positions, orientations et vitesses possibles de l'hélicoptère, les actions sont les mouvements des manettes de commande, et les récompenses sont un plus un pour un vol réussi et un moins 1 000 pour un crash.

De même, aux échecs, les états sont la position de toutes les pièces sur l'échiquier, les actions sont les coups légaux, et les récompenses sont plus un pour une victoire, moins un pour une défaite et zéro pour une égalité.

Le formalisme du processus de décision markovien est nommé d'après la propriété selon laquelle l'avenir dépend uniquement de l'état actuel et non du passé. En d'autres termes, la décision de l'agent ne considère que l'état actuel et non la manière dont il y est parvenu. L'agent choisit des actions en fonction d'une politique, qui est une fonction qui mappe les états aux actions. Après avoir pris une action, l'agent observe le nouvel état et la récompense associée, et le processus se répète.

Pour développer un algorithme permettant de choisir de bonnes actions, une quantité clé est la fonction de valeur état-action, qui estime le retour attendu en prenant une action dans un état donné et en suivant une politique par la suite. L'agent apprend à calculer cette fonction et l'utilise pour mettre à jour sa politique afin d'améliorer sa prise de décision.

Fonction de valeur d'état et action

La fonction de valeur d'état-action, notée Q, est une fonction qui prend en entrée un état et une action, et fournit un nombre qui représente le retour si l'agent commence dans cet état, prend l'action spécifiée une fois, puis se comporte de manière optimale par la suite. Le comportement optimal est celui qui donne le retour le plus élevé possible. Il peut sembler étrange que nous ayons besoin de calculer Q alors que nous connaissons déjà la politique optimale, mais nous verrons plus tard comment résoudre cette circularité.

Tout d'abord, définissons la fonction Q de manière plus précise. C'est une fonction de la paire état-action (S, A) qui donne le retour attendu si nous commençons dans l'état S, prenons l'action A, puis suivons la politique optimale par la suite. Mathématiquement, nous pouvons l'écrire comme :

Q(S, A) = E[R | S, A],

où R est le retour, et E[R | S, A] représente la valeur attendue de R étant donné que nous commençons dans l'état S, prenons l'action A, puis suivons la politique optimale. Notez que R est une variable aléatoire qui dépend de la politique, donc la valeur attendue dépend également de la politique.

Prenons un exemple. Dans l'application Mars Rover avec un facteur de réduction de 0,5, la politique optimale consiste à aller à gauche depuis les états 2, 3 et 4 et à aller à droite depuis l'état 5. Pour calculer Q de S, A, nous devons trouver le retour total en partant de l'état S, en prenant l'action A une fois, puis en se comportant de manière optimale par la suite selon la politique. Par exemple, si nous sommes dans l'état 2 et prenons l'action d'aller à droite, nous arrivons à l'état 3 et allons ensuite à gauche depuis l'état 3, puis à gauche depuis l'état 2. Finalement, nous obtenons une récompense de 100. Par conséquent, Q de l'état 2 et en allant à droite est égal au retour, qui est zéro plus 0,5 fois cela plus 0,5 au carré fois cela plus 0,5 au cube fois 100, soit 12,5.

Prenons maintenant un exemple. Supposons que nous avons un monde en grille simple avec quatre états : A, B, C et D. Chaque état a deux actions disponibles : monter ou aller à droite. Les récompenses sont les suivantes :

Monter depuis l'état A ou B donne une récompense de 0, et aller à droite donne une récompense de 1.
Monter ou aller à droite depuis l'état C donne une récompense de 5.
Monter ou aller à droite depuis l'état D donne une récompense de 10.

Le facteur de réduction est de 0,9, ce qui signifie que les récompenses futures sont réduites de 0,9 pour chaque pas de temps.

Nous pouvons calculer les valeurs Q pour chaque paire état-action comme suit. Commençons par l'état A et l'action haut. Si nous prenons cette action, nous finissons à nouveau à l'état A et recevons une récompense de 0. Le retour attendu est donc :

Q(A, haut) = E[R | A, haut] = 0 + 0,9 * Q(A, haut) + 0,1 * Q(B, haut), où le premier terme est la récompense immédiate, le deuxième terme est la récompense future actualisée si nous restons dans l'état A et prenons à nouveau l'action haut, et le troisième terme est la récompense future actualisée si nous passons à l'état B et prenons l'action haut là-bas. Nous pouvons écrire de manière similaire les valeurs Q pour les autres paires état-action :

Q(A, droite) = E[R | A, droite] = 1 + 0,9 * Q(B, droite) + 0,1 * Q(A, droite),
Q(B, haut) = E[R | B, haut] = 0 + 0,9 * Q(A, haut) + 0,1 * Q(C, haut),
Q(B, droite) = E[R | B, droite] = 1 + 0,9 * Q(C, droite) + 0,1 * Q(B, droite),
Q(C, haut) = E[R | C, haut] = 5 + 0,9 * Q(B, haut) + 0,1 * Q(D, haut),
Q(C, droite) = E[R | C, droite] = 5 + 0,9 * Q(D, droite) + 0,1 * Q(C, droite),
Q(D, haut) = E[R | D, haut] = 10 + 0,9 * Q(C, haut) + 0,1 * Q(D, haut),
Q(D, droite) = E[R | D, droite] = 10 + 0,9 * Q(D, droite) + 0,1 * Q(C, droite).

Nous pouvons résoudre ce système d'équations en utilisant des méthodes itératives ou l'inversion de matrice pour trouver les valeurs Q pour chaque paire état-action. Une fois que nous avons les valeurs Q, nous pouvons les utiliser pour déterminer la politique optimale, qui est l'action qui maximise la valeur Q pour chaque état. Dans ce cas, la politique optimale est la suivante :

À l'état A, prendre l'action droite.
À l'état B, prendre l'action droite.
À l'état C, prendre l'action haut.
À l'état D, prendre l'action haut.

Nous pouvons voir que cette politique correspond au choix de l'action ayant la valeur Q la plus élevée pour chaque état. Par exemple, dans l'état A, la valeur Q pour prendre l'action droite est de 1, ce qui est supérieur à la valeur Q pour prendre l'action haut (qui est 0). Par conséquent, la politique optimale est de prendre l'action droite à l'état A.

En résumé, la fonction Q nous permet de calculer le rendement attendu pour chaque paire état-action, ce qui est essentiel pour déterminer la politique optimale. Dans l'exemple ci-dessus, nous avons utilisé la fonction Q pour trouver la politique optimale pour un monde de grille simple. Nous pouvons utiliser des techniques similaires pour résoudre des problèmes d'apprentissage par renforcement plus complexes.

Les équations de Bellman

Si vous pouvez calculer la fonction de valeur d'état-action Q de S, A, vous pouvez déterminer la meilleure action à prendre à partir de n'importe quel état donné en sélectionnant l'action A qui donne la plus grande valeur de Q de S, A. Cependant, la question est de savoir comment calculer ces valeurs de Q de S,A ? En apprentissage par renforcement, l'équation de Bellman est une équation clé qui aide à calculer la fonction de valeur d'état-action.

Pour expliquer l'équation de Bellman, reformulons l'équation de Bellman pour la valeur Q d'une manière légèrement différente, ce qui pourrait rendre les mathématiques un peu plus claires. Rappelons que Q(S,A) représente la récompense cumulative attendue si nous commençons dans l'état S, prenons l'action A, puis suivons la politique optimale à partir de ce point. Ensuite, nous pouvons écrire l'équation de Bellman comme suit :

Q(S,A) = E[R(S,A) + γ * max(Q(S', A'))],

où E[] représente l'espérance, R(S,A) est la récompense immédiate obtenue lors de la prise de l'action A dans l'état S, γ est le facteur de réduction (qui détermine le poids à accorder aux récompenses futures), max(Q(S', A')) représente la récompense cumulative attendue maximale que nous pouvons obtenir à partir de l'état suivant S' en prenant n'importe quelle action possible A', et Q(S', A') représente la récompense cumulative attendue si nous commençons dans l'état S', prenons l'action A', puis suivons la politique optimale à partir de ce point.

Considérons maintenant un exemple. Supposons que nous avons un problème de grille simple, où l'agent peut se déplacer vers le haut, le bas, la gauche ou la droite, et chaque mouvement a une récompense de -1. Il y a également un état final spécial qui a une récompense de +10. Le facteur de réduction γ est fixé à 0,9. Voici un diagramme de la grille :

 --------------
|  |  |  | 10|
--------------
|  | -1|  | -1|
--------------
|  |  |  | -1|
--------------
|  | -1|  | -1|
--------------

Supposons que nous voulions calculer la valeur Q pour l'état (1,1) (c'est-à-dire le coin supérieur gauche) et l'action "droite". Pour ce faire, nous appliquons l'équation de Bellman comme suit:

Q(1,1,"droite") = E[R(1,1,"droite") + γ * max(Q(S', A'))]

= E[-1 + 0,9 * max(Q(1,2,"haut"), Q(2,1,"gauche"), Q(1,1,"bas"))]

= -1 + 0,9 * max(Q(1,2,"haut"), Q(2,1,"gauche"), Q(1,1,"bas")),

où nous avons utilisé le fait que la récompense immédiate pour se déplacer vers la droite à partir de l'état (1,1) est -1, et nous avons considéré tous les états et actions possibles.

Maintenant, supposons que nous ayons déjà calculé les valeurs Q pour tous les autres états et actions. Voici un tableau des valeurs Q que nous avons calculées jusqu'à présent :

 ---------------------
|  | up | dwn| lft| rt |
---------------------
| 1|  6 |  7 |  5 |  ? |
---------------------
| 2|  1 |  ? |  2 |  6 |
---------------------
| 3|  0 |  1 |  1 |  1 |
---------------------
| 4|  ? |  2 |  ? |  2 |
---------------------

Notez que la valeur Q pour l'état (1,1) et l'action "droite" est actuellement inconnue et est représentée par "?". Nous voulons utiliser l'équation de Bellman pour calculer cette valeur Q. Pour ce faire, nous évaluons d'abord les valeurs Q pour tous les états et actions possibles :

Q(1,2,"haut") = 7 Q(2,1,"gauche") = 1 Q(1,1,"bas") = 5

Ensuite, nous substituons ces valeurs dans l'équation de Bellman et obtenons :

Q(1,1,"droite") = -1 + 0,9 * max(7, 1, 5)

= -1 + 0,9 * 7

= 5,3.

Ainsi, la valeur Q pour l'état (1,1) et l'action "droite" est de 5,3. Nous pouvons mettre à jour notre tableau en conséquence :

 ---------------------
|  | up | dwn| lft| rt |
---------------------
| 1|  6 |  7 |  5 |  5.3 |
---------------------
| 2|  1 |  ? |  2 |  6 |
---------------------
| 3|  0 |  1 |  1 |  1 |
---------------------
| 4|  ? |  2 |  ? |  2 |
---------------------

Nous pouvons répéter ce processus pour toutes les autres valeurs Q inconnues jusqu'à ce que nous ayons calculé les valeurs Q pour tous les états et actions.

En résumé, l'équation de Bellman fournit un moyen de calculer les valeurs Q pour tous les états et actions dans un problème d'apprentissage par renforcement, donné les récompenses et la politique optimale. Nous pouvons utiliser cette équation pour mettre à jour de manière itérative les valeurs Q jusqu'à ce qu'elles convergent vers leurs valeurs réelles. Le processus de mise à jour itérative des valeurs Q est appelé itération de la valeur, et c'est l'un des algorithmes d'apprentissage par renforcement les plus courants.

Espace d'état continu

Lors de la conception de véhicules autonomes ou d'autres systèmes robotiques, il est important de prendre en compte l'espace d'état dans lequel le système opère. Dans le cas d'un rover sur Mars, l'espace d'état est discret et ne comprend que six positions possibles. Cependant, pour la plupart des systèmes robotiques, l'espace d'état est continu et peut prendre n'importe quel nombre de valeurs dans une plage donnée.

Par exemple, supposons que nous avons un système qui peut se déplacer le long d'une ligne, et sa position est indiquée par un nombre allant de 0 à 1. C'est un exemple d'espace d'état continu, car n'importe quel nombre entre 0 et 1 est une position valide pour le système. En revanche, si le système ne pouvait être que dans l'une des deux positions - disons, 0 ou 1 - alors l'espace d'état serait discret.

Lorsque l'on travaille avec des vecteurs dans des espaces d'état continus, chaque composante du vecteur peut être représentée à l'aide d'un nombre réel. Par exemple, si nous avons un système qui peut se déplacer en deux dimensions, son état pourrait être représenté par un vecteur (x, y), où x et y sont tous deux des nombres réels. Toute combinaison de valeurs réelles pour x et y dans une plage valide serait un état valide pour le système.

En apprentissage par renforcement, l'espace d'état est souvent utilisé pour représenter l'état actuel du système, et l'espace d'action est utilisé pour représenter l'ensemble des actions possibles que le système peut prendre. L'objectif de l'algorithme d'apprentissage par renforcement est de trouver une politique optimale - c'est-à-dire une correspondance entre les états et les actions - qui maximise une fonction d'objectif, telle que la récompense totale obtenue au fil du temps.

Par exemple, supposons que nous avons un bras robotique qui peut se déplacer en trois dimensions. Son état pourrait être représenté par un vecteur (x, y, z), où x, y et z sont tous des nombres réels représentant la position du bras dans l'espace tridimensionnel. L'espace d'action pourrait être représenté par un autre vecteur (dx, dy, dz), où dx, dy et dz sont tous des nombres réels représentant le changement de position du bras dans chaque dimension. L'algorithme d'apprentissage par renforcement tenterait alors de trouver une politique optimale qui associe chaque état à une action, afin d'atteindre un objectif souhaité, tel que l'atteinte d'un emplacement particulier dans l'espace ou l'évitement d'obstacles.

Exemple de simulation Lunar Lander

Prenons un exemple : lunar lander

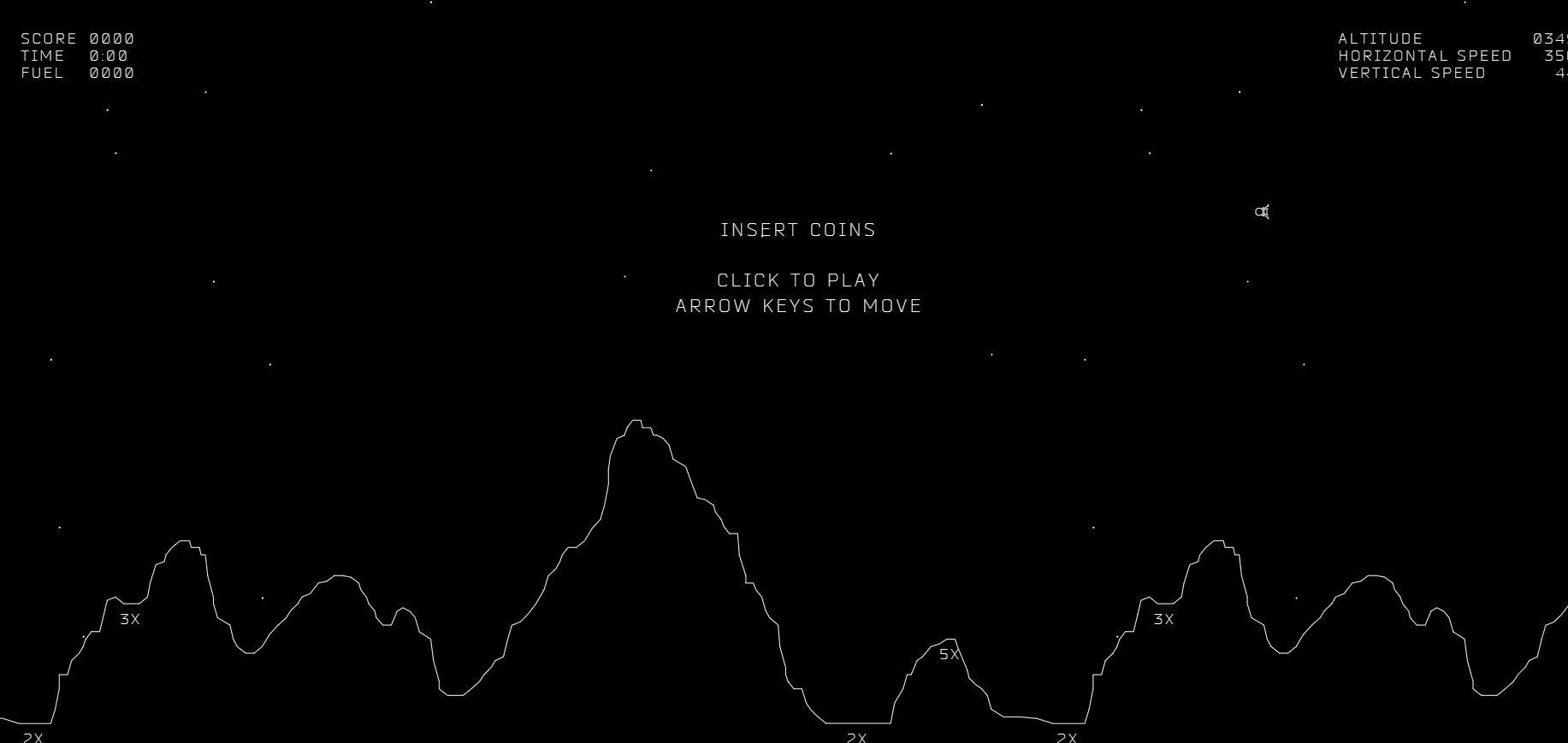
Le Lunar Lander est une simulation qui permet aux chercheurs d'étudier l'apprentissage par renforcement. Il est similaire à un jeu vidéo, où vous contrôlez un atterrisseur lunaire qui descend rapidement vers la surface de la lune. Votre objectif est de le faire atterrir en toute sécurité sur la plateforme d'atterrissage en utilisant les propulseurs aux moments appropriés.

Regardons de plus près comment fonctionne la simulation Lunar Lander. Vous contrôlez un atterrisseur lunaire qui descend rapidement vers la surface de la lune. Votre objectif est de le faire atterrir en toute sécurité sur la plateforme d'atterrissage en utilisant les propulseurs aux moments appropriés.

Il y a quatre actions possibles dans la simulation : "rien", "gauche", "principal" et "droite". Si vous ne faites rien, l'atterrisseur lunaire sera attiré vers la surface de la lune par les forces d'inertie et de gravité. Si vous utilisez le propulseur gauche, l'atterrisseur se déplacera vers la droite. Si vous utilisez le propulseur droit, l'atterrisseur se déplacera vers la gauche. Si vous utilisez le moteur principal, l'atterrisseur poussera vers le bas.

Le vecteur d'état de l'atterrisseur lunaire comprend sa position, sa vitesse, son angle, et s'il y a une jambe gauche ou droite posée sur le sol. La position indique la distance à gauche ou à droite et la hauteur de l'atterrisseur. La vitesse indique la vitesse à laquelle l'atterrisseur se déplace dans les directions horizontale et verticale. L'angle indique l'inclinaison de l'atterrisseur vers la gauche ou la droite. Les variables l et r indiquent si la jambe gauche ou droite touche le sol, et elles ont une valeur binaire et ne peuvent prendre que les valeurs de zéro ou un.

La fonction de récompense de la simulation est conçue pour encourager les comportements souhaités par les concepteurs et décourager ceux qu'ils ne veulent pas. Si l'atterrisseur atterrit en toute sécurité sur la plateforme d'atterrissage, il reçoit une récompense entre 100 et 140, en fonction de sa performance. Si l'atterrisseur se rapproche de la plateforme d'atterrissage, il reçoit une récompense positive, et s'il s'éloigne, il reçoit une récompense négative. S'il y a une collision, l'atterrisseur reçoit une grosse récompense négative de -100. S'il y a un atterrissage en douceur (c'est-à-dire pas de collision), il reçoit une récompense de +100 pour chaque jambe posée sur le sol. Il reçoit également une récompense de +10 pour chaque jambe posée sur le sol, et enfin, il reçoit une récompense négative chaque fois qu'il utilise les propulseurs latéraux gauche ou droit (-0,03) ou le moteur principal (-0,3).

Le but du problème du Lunar Lander est d'apprendre une politique π qui sélectionne l'action optimale a pour un état donné s. La politique π doit maximiser la somme des récompenses actualisées, qui est calculée à l'aide du paramètre gamma. Pour la simulation Lunar Lander, une valeur de gamma de 0,985 est utilisée. L'algorithme d'apprentissage utilisé pour trouver la politique optimale implique l'utilisation de l'apprentissage profond ou les réseaux de neurones pour approximer la fonction de politique optimale. L'algorithme d'apprentissage met à jour de manière itérative la fonction de politique en fonction des états et des récompenses observés, en utilisant des techniques telles que l'apprentissage par renforcement Q, les méthodes de gradient de politique, ou les méthodes de l'acteur-critique. L'objectif est de trouver une politique qui peut faire atterrir avec succès l'atterrisseur lunaire sur la plateforme d'atterrissage avec la plus grande récompense totale possible, tout en minimisant l'utilisation de carburant et en évitant les collisions. Le problème du Lunar Lander est une application stimulante et passionnante de l'apprentissage par renforcement, avec de nombreuses applications dans le monde réel telles que le contrôle de robots, la conduite autonome, et les jeux.

Apprentissage de la fonction état-action

L'apprentissage par renforcement est un type d'apprentissage automatique dans lequel un agent apprend à prendre des décisions en interagissant avec son environnement. L'agent reçoit des récompenses ou des punitions de l'environnement en fonction de ses actions, et il apprend à maximiser les récompenses au fil du temps en ajustant son comportement.

Dans l'exemple du Lunar Lander, l'agent est le réseau de neurones, et l'environnement est la simulation du Lunar Lander. L'objectif de l'agent est d'apprendre une politique qui lui indique quelle action prendre dans chaque état pour maximiser sa récompense totale. La politique est apprise en estimant la fonction Q valeur état-action, qui donne la récompense totale attendue pour prendre une action particulière dans un état particulier et suivre la politique optimale par la suite.

L'idée clé derrière l'algorithme d'apprentissage par renforcement utilisé dans cet exemple est d'utiliser les équations de Bellman pour créer un ensemble d'exemples d'états-actions-récompenses auxprochains états, puis de former un réseau de neurones pour approximer la fonction Q valeur état-action en utilisant l'apprentissage supervisé.

Les équations de Bellman sont un ensemble d'équations récursives qui relient la valeur d'un état ou d'une paire état-action aux valeurs de ses états ou paires état-action voisins. Dans le contexte de l'exemple du Lunar Lander, l'équation de Bellman pour la fonction Q valeur état-action est :

Q(s,a) = R(s) + γ max_a' Q(s',a')

où s est l'état actuel, a est l'action actuelle, R(s) est la récompense immédiate pour prendre l'action a dans l'état s, γ est un facteur de réduction qui échange les récompenses immédiates contre les récompenses futures, s' est le prochain état, et max_a' Q(s',a') est la récompense attendue maximale pour toute action a' dans le prochain état s'.

Pour former le réseau de neurones pour approximer Q, nous utilisons les tuples état-action-récompense-prochain état que nous recueillons en interagissant avec l'environnement. Chaque tuple se compose d'une paire état-action (s,a), d'une récompense immédiate R(s) et du prochain état s'. Nous utilisons ces tuples pour créer un ensemble d'exemples de formation avec des entrées x = (s,a) et des cibles y = R(s) + γ max_a' Q(s',a'). Nous formons ensuite le réseau de neurones pour minimiser l'erreur quadratique moyenne entre ses prédictions pour y et les vraies valeurs de y.

Par exemple, supposons que nous avons le tuple suivant :

s = [0,5, -0,2, 0,3, 0,7, 0,2, 1, 0, 1] a = [0, 1, 0, 0] r = 10 s' = [0,6, -0,1, 0,2, 0,6, 0,3, 1, 0, 1]

Nous utiliserions ce tuple pour créer un exemple de formation avec des paramètres aléatoires, nous utilisons un tampon de lecture pour stocker les tuples d'expérience les plus récents, qui se composent de l'état actuel, de l'action entreprise, de la récompense obtenue et de l'état suivant. Ces tuples d'expérience sont utilisés pour créer un ensemble d'entraînement de paires d'entrée-sortie (x, y), où x est la paire état-action et y est la valeur Q cible calculée à l'aide de l'équation de Bellman.

Pour être plus précis, l'équation de Bellman indique que la valeur Q pour une paire état-action (s, a) est égale à la récompense immédiate pour cette action plus la valeur Q maximale actualisée pour l'état suivant (s') et toutes les actions possibles (a'). Mathématiquement, cela peut être écrit comme :

Q(s, a) = r + γ * max(Q(s', a'))

où r est la récompense immédiate pour l'action a dans l'état s, γ (gamma) est un facteur d'actualisation qui détermine l'importance des récompenses futures, et max(Q(s', a')) est la valeur Q maximale pour toutes les actions possibles a' dans l'état suivant s'.

Pendant l'entraînement, nous utilisons le tampon de lecture pour échantillonner aléatoirement un lot de tuples d'expérience (s, a, r, s') à partir du tampon, et les utilisons pour mettre à jour les paramètres du réseau Q. Le but est de minimiser la différence entre la valeur Q prédite et la valeur Q cible, qui est donnée par l'équation de Bellman.

Pour y parvenir, nous utilisons une fonction de perte qui mesure l'erreur quadratique moyenne entre la valeur Q prédite et la valeur Q cible pour chaque paire état-action dans le lot. Mathématiquement, la fonction de perte peut être écrite comme :

L = 1/N * Σ[(y - Q(s, a))^2]

où N est la taille du lot, y est la valeur Q cible calculée à l'aide de l'équation de Bellman, et Q(s, a) est la valeur Q prédite pour la paire état-action (s, a).

Le réseau neuronal est entraîné à l'aide de la descente de gradient pour minimiser la fonction de perte, et les paramètres du réseau Q sont mis à jour après chaque itération d'entraînement. En répétant ce processus avec différents lots de tuples d'expérience, le réseau Q apprend progressivement à approximer la fonction Q optimale pour la tâche donnée.

Par exemple, dans le cas du problème Lunar Lander, le réseau Q prend en entrée l'état actuel du module lunaire et les actions possibles, et renvoie la valeur Q pour chaque action. Pendant l'entraînement, le réseau Q est mis à jour à l'aide de lots de tuples d'expérience qui se composent de l'état actuel, de l'action entreprise, de la récompense obtenue et de l'état suivant. Au fil du temps, le réseau Q apprend à approximer la fonction Q optimale, qui peut être utilisée pour sélectionner la meilleure action pour l'état actuel du module lunaire.

Greedy Policy

La fonction Q est définie comme Q(s, a) = E[R + γ maxa' Q(s', a')], où R est la récompense immédiate, γ est le facteur d'actualisation et s' est l'état suivant résultant de l'action a prise dans l'état s.

Le but de l'algorithme d'apprentissage est d'estimer la fonction Q et d'apprendre la politique optimale qui maximise la récompense cumulative attendue. Une approche courante consiste à utiliser un réseau neuronal pour approximer la fonction Q, avec l'entrée étant l'état et l'action, et la sortie étant la valeur Q estimée.

La politique Epsilon-greedy peut être formalisée comme suit :

Avec une probabilité Epsilon, sélectionnez une action aléatoire.
Avec une probabilité 1 - Epsilon, sélectionnez l'action qui maximise la valeur Q estimée pour l'état actuel.

Par exemple, supposons que nous avons un environnement lunar lander avec quatre actions possibles : allumer le propulseur principal, allumer le propulseur gauche, allumer le propulseur droit et ne rien faire. Si nous fixons Epsilon à 0,1, alors 10 % du temps, nous choisirons une action aléatoire, et 90 % du temps, nous choisirons l'action ayant la plus grande valeur Q estimée.

Supposons que l'état actuel est tel que les valeurs Q estimées pour les quatre actions sont les suivantes : Q(s, main) = 0,5, Q(s, left) = 0,8, Q(s, right) = 0,6 et Q(s, none) = 0,2. Avec une probabilité de 0,9, nous choisirons l'action "left" car elle a la valeur Q estimée la plus élevée. Avec une probabilité de 0,1, nous choisirons une action aléatoire, qui pourrait être l'une des quatre actions.

Le choix d'Epsilon est crucial pour équilibrer l'exploration et l'exploitation. Une valeur élevée d'Epsilon signifie que l'agent explorera davantage et essayera de nouvelles actions, ce qui peut être utile dans les premiers stades de l'apprentissage lorsque les valeurs Q ne sont pas encore précises. Cependant, une faible valeur d'Epsilon signifie que l'agent exploitera les connaissances actuelles et choisira l'action qui est censée donner la plus grande récompense.

En pratique, il est courant de commencer avec une valeur élevée d'Epsilon et de la diminuer progressivement au fil du temps à mesure que l'agent en apprend davantage sur l'environnement. Cela est souvent appelé un calendrier d'annealing Epsilon-greedy. Par exemple, nous pourrions commencer avec Epsilon = 1,0 et le diminuer légèrement après chaque épisode jusqu'à ce qu'il atteigne une valeur minimale.

Les limites de l'apprentissage par renforcement

L'apprentissage par renforcement est une technologie passionnante qui suscite un grand intérêt de ma part. Cependant, il y a souvent beaucoup d'excitation autour de l'apprentissage par renforcement et de son utilité pour les applications pratiques. Dans cette section, mon objectif est de fournir une perspective pratique sur la place qu'occupe l'apprentissage par renforcement aujourd'hui.

Une des raisons de l'excitation autour de l'apprentissage par renforcement est que de nombreuses publications de recherche se sont concentrées sur des environnements simulés. Bien que ces simulations puissent être utiles pour les tests et la prototypage, il est important de noter que l'obtention d'algorithmes d'apprentissage par renforcement pour fonctionner dans le monde réel peut être beaucoup plus difficile. Cela est particulièrement vrai pour les applications impliquant des robots physiques. Par conséquent, il est important de prêter attention à cette limitation et de s'assurer que tout algorithme d'apprentissage par renforcement est testé et validé dans le monde réel.

Malgré la couverture médiatique autour de l'apprentissage par renforcement, il est également important de noter qu'il existe actuellement moins d'applications pratiques d'apprentissage par renforcement que d'apprentissage supervisé et non supervisé. Par conséquent, si vous construisez une application pratique, il est plus probable que l'apprentissage supervisé ou non supervisé sera l'outil approprié pour le travail. Bien que l'apprentissage par renforcement puisse être utile pour certaines applications, ce n'est pas toujours l'approche la plus appropriée.

L'apprentissage par renforcement reste l'un des principaux piliers de l'apprentissage machine, et c'est un domaine de recherche passionnant avec beaucoup de potentiel pour les applications futures. En développant vos propres algorithmes d'apprentissage machine, l'intégration de l'apprentissage par renforcement en tant que cadre peut vous aider à construire des systèmes plus efficaces. Bien qu'il puisse être difficile d'obtenir des algorithmes d'apprentissage par renforcement pour fonctionner dans le monde réel, voir vos algorithmes accomplir avec succès une tâche telle que l'atterrissage en sécurité d'un atterrisseur lunaire sur la lune peut être une expérience enrichissante.