L'apprentissage par renforcement

En Machine Learning, nous définissons un environnement dans lequel notre intelligence artificielle (IA) va prendre des actions, apprendre et évoluer. Ainsi, notre "agent", qui sera notre IA, prendra des actions et obtiendra des récompenses (et des états) en fonction de ces actions.

Le but du Machine Learning est de permettre à l'agent d'apprendre à prendre les meilleures actions possibles dans cet environnement afin d'optimiser ses récompenses à long terme. Cela nécessite une exploration active de l'environnement par l'agent afin de découvrir les actions qui maximiseront ses récompenses à long terme.

Ainsi, l'agent saura, dans un environnement, comment une action peut lui rapporter une récompense et quelles actions ne lui en rapporteront pas. Comme dans la vraie vie, lorsque nous réalisons des actions, nous sommes récompensés pour nos actions réussies, mais nous apprenons également de nos erreurs pour progresser vers nos objectifs.

L'équation de Bellman est en effet un principe fondamental de l'apprentissage par renforcement. Elle permet de formaliser le calcul de la récompense attendue par l'agent pour une action donnée dans un état donné de l'environnement.

L'équation de Bellman

Commençons:

• S : État (state)
• S' : État final (final state)
• A : Action
• R : Récompense (reward)
• Y : Remise (discount)

Prenons l'exemple d'un agent qui doit se rendre à un point d'arrivée :

Lorsqu'un agent effectue une action (A) dans un état (S), il reçoit une récompense (R) et se retrouve dans un nouvel état (S'). Le but de l'agent est de maximiser la somme des récompenses qu'il reçoit tout au long de ses actions, en prenant en compte le fait que les récompenses futures sont remises (discounted) par un facteur Y. Ainsi, l'agent doit apprendre à choisir les meilleures actions dans chaque état pour maximiser la somme des récompenses qu'il recevra jusqu'à atteindre l'état final (S').

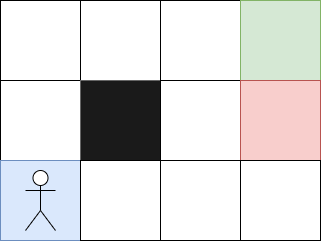
Ici, si l'agent se rend sur la case rouge, il recevra un malus, et s'il arrive sur la case verte, il recevra une récompense. La case noire ne peut pas être franchie. Dans un premier temps, l'agent prendra des actions aléatoires car il ne saura pas quoi faire. Puis, il apprendra progressivement quelles actions prendre pour atteindre le point d'arrivée.

Chaque étape pour atteindre la case finale aura une valeur de 1. Ces valeurs permettront alors à l'agent de reproduire le chemin à l'infini.

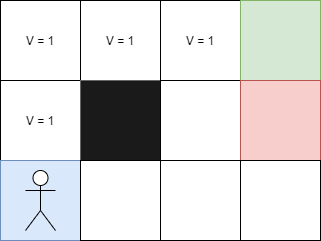
Mais que se passe-t-il si l'agent change de place et commence en haut à gauche ? Dans ce cas-là, l'approche ne fonctionne pas spécialement bien. Pour remédier à cela, il convient d'utiliser l'équation de Bellman :

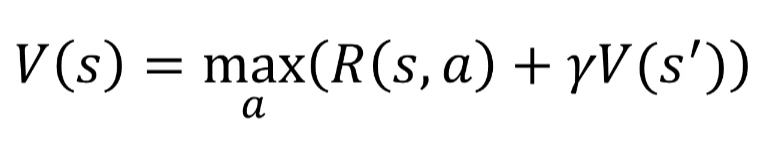
Dans notre problème précédent, chaque case correspond à un état. Ainsi, si je prends le carré suivant, quelle sera sa valeur ?

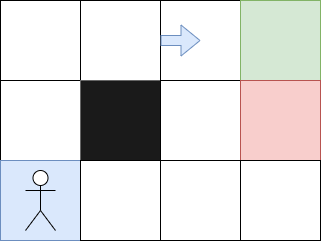
Considérons l'exemple suivant : la récompense pour aller à droite est de +1 car cela correspond à l'arrivée. Comme nous sommes à la fin, il n'y a pas de remise à appliquer et la valeur de cet état est donc de V = 1.

Maintenant, prenons la case de gauche : la récompense pour aller à droite est de 0 car cette case blanche ne donne pas de récompense. On applique la remise Y de 0,9 (valeur arbitraire choisie ici) à la valeur de l'état suivant, qui est de 1, et nous obtenons Y * V de la case suivante, soit 0,9 * 1 = 0,9. Ainsi, la valeur de cet état est de V = 0,9.

Poursuivons avec la case de gauche : si nous allons à droite, nous n'aurons pas de récompense car il s'agit d'une case blanche. Nous appliquons la remise Y de 0,9 à la valeur de l'état suivant à droite, qui est de 0,9, et nous obtenons Y * V de la case suivante, soit 0,9 * 0,9 = 0,81. Ainsi, la valeur de cet état est de V = 0,81.

Et ainsi de suite pour calculer la valeur de chaque état en utilisant l'équation de Bellman, qui permet de calculer la valeur d'un état en fonction de la récompense obtenue pour l'action entreprise dans cet état et de la valeur des états suivants pondérée par la remise Y.

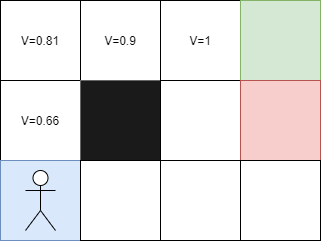
Voici une correction de l'orthographe et une proposition de réécriture pour développer une structure plus claire et facile à comprendre concernant l'équation de Bellman :

Ainsi, plus je m'éloigne de l'arrivée, plus la valeur de V diminue, ce qui est normal. Désormais, chaque case a une valeur plus grande si elle est proche de l'arrivée et donc je peux commencer sur n'importe quelle case.

Mais quelle est la valeur de la case à gauche de la case rouge ? Étant donné qu'il est impossible d'aller à gauche depuis la case rouge, nous avons trois directions possibles. Si je vais vers le haut, j'aurai une valeur V de 0,9 car nous savons que la case du haut a une valeur de 1.

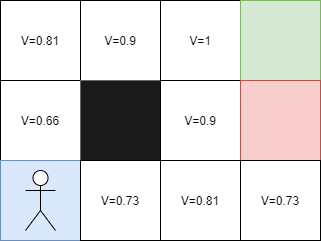
L'équation de Bellman permet de calculer la valeur d'un état en fonction de la récompense obtenue pour l'action entreprise dans cet état et de la valeur des états suivants pondérée par la remise Y. Plus l'agent s'éloigne de l'arrivée, plus la valeur de l'état diminue, et inversement, plus l'agent se rapproche de l'arrivée, plus la valeur de l'état augmente. Ainsi, en utilisant cette équation, nous pouvons calculer la valeur de chaque état et déterminer la meilleure action à prendre dans chaque état pour maximiser les récompenses obtenues.

Le plan et Markov

Le plan consiste à remplacer les valeurs des cases par des flèches pour obtenir le chemin optimal. Pour ce faire, nous évaluons la direction à prendre à partir d'une case en regardant la case adjacente qui a la valeur la plus élevée. Cela nous permet de déterminer les directions résultant de l'équation de Bellman et d'obtenir un chemin clair pour notre agent.

Cependant, est-ce que cela suffit pour définir l'intelligence artificielle ? Pas du tout ! Nous devons parler des processus impliqués.

Dans un processus déterministe, si l'agent se déplace vers le haut, il aura une probabilité de 100% d'y arriver car il s'y dirige directement. Cependant, dans un processus non déterministe, il y a une différence entre ce que l'on veut et ce qui se passe réellement. En général, nous ne pouvons pas prédire à 100% ce qui va se passer.

Le processus de Markov est un processus stochastique dans lequel le futur ne dépend que de l'état présent et non pas des états passés. Ainsi, toutes les actions passées n'ont aucune influence sur l'état actuel. Dans le processus de décision Markovien (MDP), l'agent ne peut pas contrôler complètement le résultat de sa décision, mais il peut choisir la décision à prendre en utilisant un processus de Markov pour déterminer la direction la plus probable à suivre.

Pour intégrer ce facteur avec l'équation de bellman :

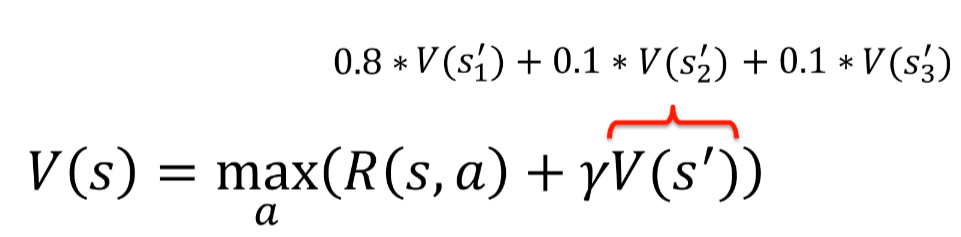
OU (plus compliqué à comprendre mais équivalent)

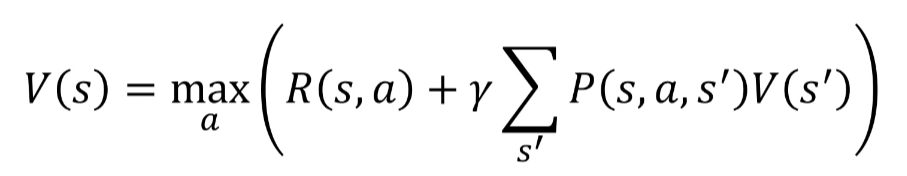
Dans l'équation de Bellman, nous utilisons la remise Y pour pondérer les valeurs des états futurs en fonction de leur probabilité d'occurrence. Ainsi, nous pouvons prendre en compte la probabilité d'arriver à un état final donné en ajoutant des probabilités d'action. Par exemple, si nous avons une probabilité qu'une action nous mène à la case rouge, nous devons prendre en compte cette probabilité dans notre schéma de décision.

Cela nous amène à nous poser les bonnes questions. Étant donné que nous avons une probabilité qu'une direction puisse nous faire tomber sur la case rouge, notre schéma de décision doit tenir compte de cette probabilité pour éviter les pertes potentielles. Ainsi, le processus de décision Markovien (MDP) est utilisé pour prendre en compte les probabilités d'occurrence et les risques potentiels dans la prise de décisions pour un agent en utilisant le processus de Markov:

Pénalité de vie

Il est important de se rappeler que dans le cadre de l'apprentissage par renforcement, l'IA reçoit une pénalité à la fin de son parcours. Cependant, dans la réalité, nous devons plutôt ajouter de petites récompenses à chaque étape pour aider l'IA à naviguer dans l'environnement. Par exemple, dans le cas d'un labyrinthe, l'agent accumulera des récompenses à chaque mouvement, ce qui l'aidera à progresser vers la sortie. Dans ce cas, les récompenses seront de -0,04 car le but de l'IA est de sortir du labyrinthe le plus rapidement possible. Ainsi, en ajoutant des récompenses à chaque étape, nous pouvons aider l'IA à trouver le meilleur chemin vers la sortie.

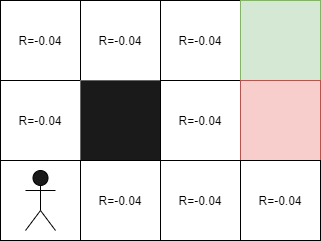
Lorsque nous ajoutons des récompenses négatives à chaque étape, notre objectif est de "presser" l'IA à trouver le chemin le plus rapide vers l'arrivée. Cependant, que se passerait-il si nous utilisions des récompenses négatives plus importantes ?

• Lorsque R(s) = 0, nous évitons la case rouge et nous prenons même le risque de foncer dans des murs pour éviter d'aller directement vers le haut, et ainsi aller vers la droite ou la gauche.

• Lorsque R(s) = -0,04, nous ne prenons plus le temps de foncer dans les murs, mais nous essayons toujours d'éviter au maximum la case rouge.

• Lorsque R(s) = -0,5, nous tentons d'aller à la case de départ par tous les moyens, même si cela signifie prendre le risque de passer près de la case rouge.

• Lorsque R(s) = -2,0, notre objectif est de terminer le jeu le plus rapidement possible, car -2 est une pénalité plus importante que celle de la case rouge. Ainsi, le moins pire peut être de tomber dans la case rouge pour terminer le jeu plus rapidement.

En utilisant des récompenses négatives plus importantes, nous poussons l'IA à prendre des risques plus importants pour atteindre son objectif le plus rapidement possible. Cela peut avoir des avantages et des inconvénients, en fonction de l'objectif de l'IA et des contraintes du problème à résoudre.

Qlearning intuition

On mesure ici une qualité quand on est dans un état (S). Ainsi :

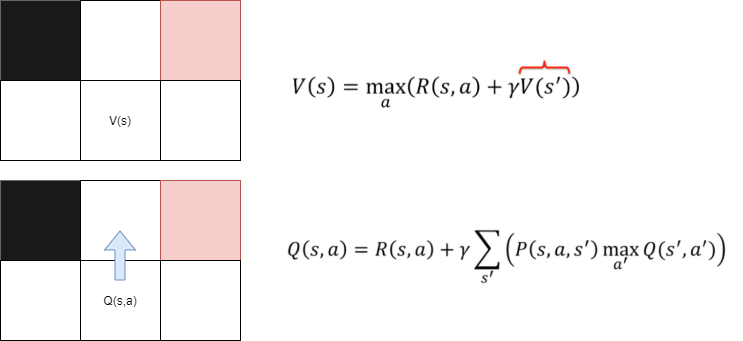
Pour calculer la valeur optimale d'une case, nous utilisons la même méthode que précédemment avec l'équation de Bellman. Nous calculons la moyenne pondérée d'arriver sur une case pour trouver la meilleure action possible.

Ainsi, la valeur de Q(s,a) est égale à la valeur de V(s), où V(s) est le maximum possible pour la case s. En utilisant Q(s,a), nous pouvons calculer la meilleure action possible pour l'état s. Cela dépend de la valeur de V(s') pour les états futurs s'. Ainsi, nous pouvons dire que la valeur de Q(s,a) dépend de la valeur de V(s') pour trouver la meilleure action à prendre.

Différence temporelle

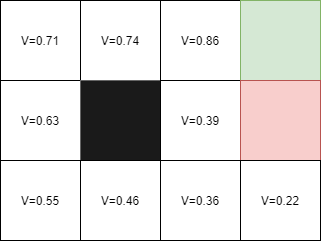
En se souvenant de la méthode déterministe et non déterministe, nous pouvons prendre l'exemple de la dernière case, dont la valeur était :

• Déterministe : V = 1, car nous avions une récompense de +1 pour atteindre cette case.
• Non déterministe : V = 0,86, avec une probabilité de 80 % d'arriver à la case finale. Pour trouver la valeur précédente de V = 0,86, nous devons calculer la valeur de V = 0,39 et ainsi de suite. Cela peut nous amener à tomber dans une boucle de calcul pour déterminer les valeurs des états.

En utilisant notre nouvelle fonction de mise à jour des valeurs, la différence temporelle, nous pouvons résoudre ce problème en mettant à jour les valeurs des états en fonction de la différence entre les valeurs actuelles et les valeurs futures. En utilisant cette méthode, nous pouvons calculer rapidement les valeurs des états sans avoir besoin de calculer toutes les valeurs précédentes. Cela nous permet d'économiser du temps et de l'énergie dans le processus d'apprentissage par renforcement.

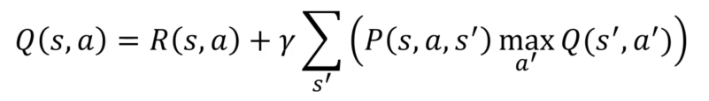
OU

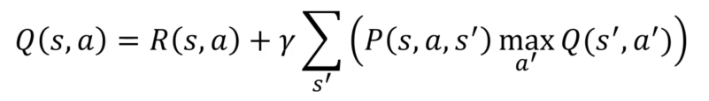
Prenons un exemple, imaginons que dans notre environnement nous démarrons commençons sur cette case :

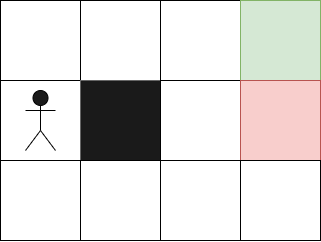
Notre IA a déjà effectué des calculs pour trouver les valeurs optimales pour chaque état. Dans le cas de notre premier essai, les valeurs initiales pour chaque état seront des valeurs aléatoires.

Avant de prendre une action, nous calculons la valeur de Q(s,a) pour trouver la meilleure action possible pour l'état actuel s. Une fois que l'action a été prise, nous utilisons la différence temporelle pour mettre à jour les valeurs des états.

Après la prise l'action nous pouvons appliquer :

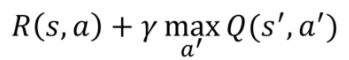
Après avoir pris une action dans l'état S, nous recevons une récompense. En utilisant cette récompense, nous pouvons calculer l'état temporel, qui est la différence entre l'état futur après avoir pris l'action et l'état actuel avant d'avoir pris l'action. Cette différence temporelle peut être écrite comme :

Lorsque la différence temporelle est égale à 0, cela signifie que la valeur de l'état actuel est égale à la somme des valeurs des états futurs pondérées par leurs probabilités et leurs récompenses, tel que défini par l'équation de Bellman. Cela peut être le cas si notre IA a été entraînée avec succès pendant un certain temps, mais ce ne sera pas toujours le cas au début.

Si nous rencontrons une situation où nous obtenons une valeur que nous n'attendions pas (par exemple, un événement aléatoire de 10 %), nous ne voulons pas perdre la valeur précédente en mettant à jour la valeur de l'état immédiatement. Pour éviter cela, nous utilisons un coefficient temporel, que nous multiplions par alpha (un paramètre entre 0 et 1). Cela nous permet de mettre à jour la valeur de l'état lentement, en donnant moins d'importance à la valeur aléatoire, tout en conservant une trace de la valeur précédente. Cela rend le processus d'apprentissage par renforcement plus robuste et plus efficace.

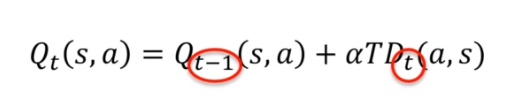
Si l'on combine tout :

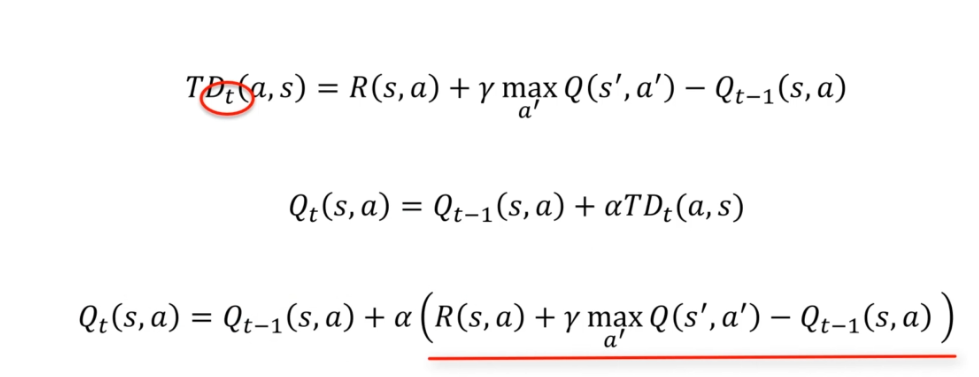
Lorsque nous utilisons le coefficient temporel alpha, nous devons trouver un équilibre entre l'exploitation des valeurs précédentes et la mise à jour des nouvelles valeurs. Si nous prenons un alpha de 0, l'expression temporelle est annulée, et l'agent ne pourra rien apprendre. Si nous prenons un alpha de 1, les valeurs précédentes de Qt-1(s, a) sont complètement annulées, et l'agent se concentre uniquement sur les nouvelles valeurs.

Nous devons donc choisir un alpha qui se situe entre ces deux extrêmes, afin de conserver une mémoire du passé et du présent. Le but est de rendre la valeur de Q aussi stable que possible, tout en gardant à l'esprit que l'environnement peut changer et que la valeur de Q peut devoir être réévaluée.

Un exemple de Q-learning pourrait être le suivant :

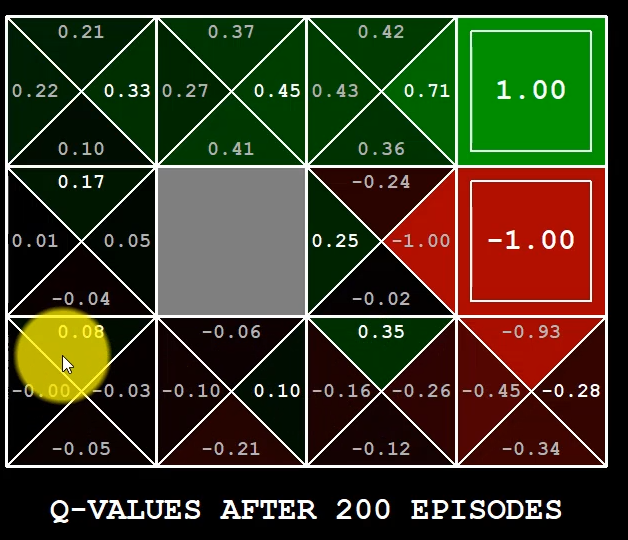
Deep learning intuition

Dans l'exemple précédent, notre agent avait des récompenses constantes en fonction de chaque action, ce qui a permis à l'agent d'attribuer des valeurs à chaque case et de développer une stratégie pour atteindre le point d'arrivée.

Cependant, dans des cas plus complexes tels que la conduite autonome, il peut y avoir de nombreux facteurs imprévus tels que des piétons, des animaux, etc. Il serait impossible de créer un état pour chaque possibilité.

Pour résoudre ce problème, nous pouvons créer des états avec deux dimensions dans le cas de notre labyrinthe, par exemple (X1, X2). Cette méthode est appelée Deep Q-Learning, et elle permet à notre agent d'apprendre à naviguer dans un environnement plus complexe en créant des états abstraits qui encapsulent plusieurs états réels. En d'autres termes, notre agent peut apprendre à identifier les situations similaires et à prendre des décisions en conséquence, même s'il n'a jamais été confronté à une situation exactement identique.

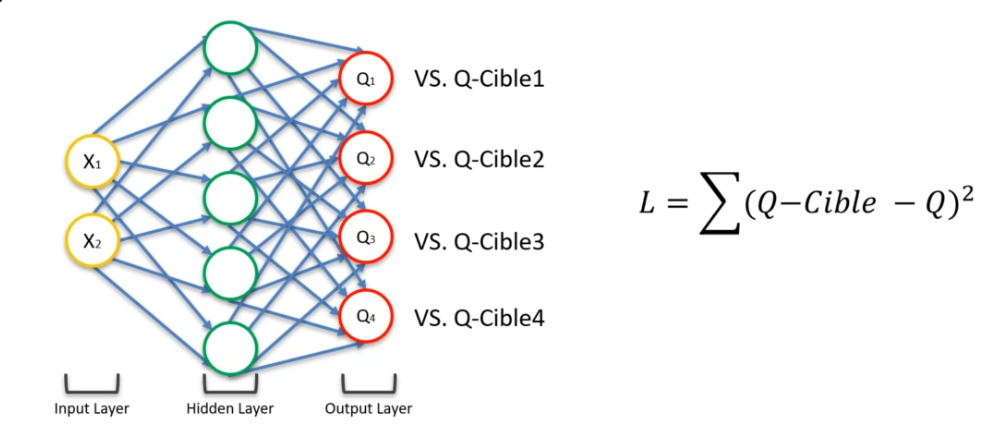
Dans le Deep Q-Learning, il n'y a plus la notion d'avant et après. Ici, le réseau de neurones va sortir 4 prédictions pour le Q(s,a) : Q1, Q2, Q3, Q4. Au début, nous n'avons pas de valeurs pour ces prédictions. Pour ce faire, nous allons récupérer les valeurs que nous avons déjà reçues grâce à l'algorithme de Bellman. Ainsi, nous pourrons comparer nos valeurs avec les Q-cibles. Nous calculerons donc une fonction de coût via ces Q-cibles. Nous ferons ensuite notre rétropropagation, ce qui mettra à jour nos poids sur nos Hidden layer.

L'expérience replay

Lorsqu'on utilise le Deep Q-Learning, le réseau de neurones peut être instable et ne pas converger facilement. De plus, il doit traiter une grande quantité d'informations en un instant. Pour remédier à ces problèmes, on utilise la technique de l'expérience replay. Cette méthode consiste à rejouer des expériences passées de manière aléatoire pour que l'agent puisse apprendre à partir de situations similaires rencontrées dans le passé.

L'expérience replay est une technique utilisée en apprentissage par renforcement pour améliorer la stabilité et la performance des algorithmes de deep Q-learning. Cette technique consiste à stocker toutes les expériences passées (observations de l'environnement, actions prises par l'agent, récompenses obtenues et états suivants) dans une mémoire tampon appelée "replay buffer".

Au lieu de mettre à jour les poids du réseau de neurones à chaque nouvelle expérience, on va sélectionner des expériences passées de manière aléatoire dans le replay buffer et les utiliser pour entraîner le réseau. Cette technique permet d'éviter que le réseau de neurones ne soit biaisé par des expériences spécifiques et d'assurer une diversité des données d'entraînement.

L'expérience replay permet de réutiliser efficacement les données d'entraînement et de minimiser le temps d'entraînement du réseau de neurones. En effet, en réutilisant les expériences passées, on limite le nombre de mises à jour nécessaires pour atteindre une performance optimale.

Stratégie de sélection d'actions

L'idée de la fonction est de trouver un juste équilibre entre l'exploration et l'exploitation. En général, on a plusieurs valeurs possibles pour une action, et l'on choisira la plus élevée. Toutefois, cela peut poser des problèmes car de nouveaux événements pourraient totalement changer la donne. Dans le cas de l'exploration, on cherche justement à trouver de nouvelles solutions qui pourraient apparaître. Ainsi, il existe plusieurs stratégies de sélection d'actions :

• ε-greedy : on choisit une valeur ε entre 0 et 1, qui représente un pourcentage. Par exemple, si ε = 10%, alors 10% du temps, on prend une décision totalement aléatoire, et le reste du temps, on prend la meilleure décision possible. Ainsi, 10% du temps, on fait de l'exploration (on teste de possibles nouveautés), et 90% du temps, on se base sur ce qu'on a appris (on fait de l'exploitation).

• ε-soft(1-ε) : cette stratégie est exactement pareille que la précédente, mais on inverse la valeur de ε. Ainsi, 90% du temps, on prend la meilleure décision possible, et 10% du temps, on fait de l'exploration.

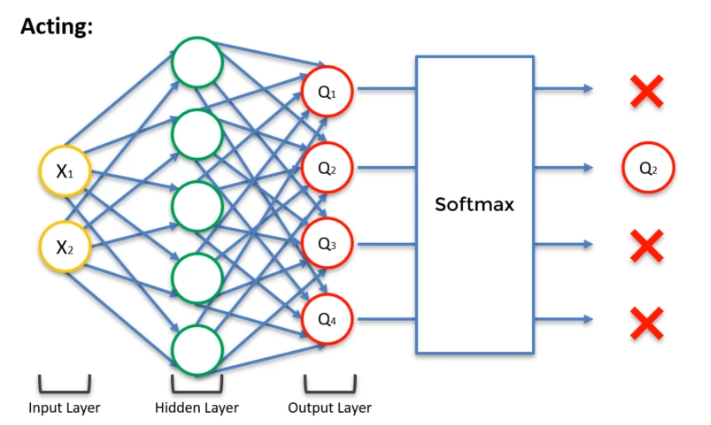
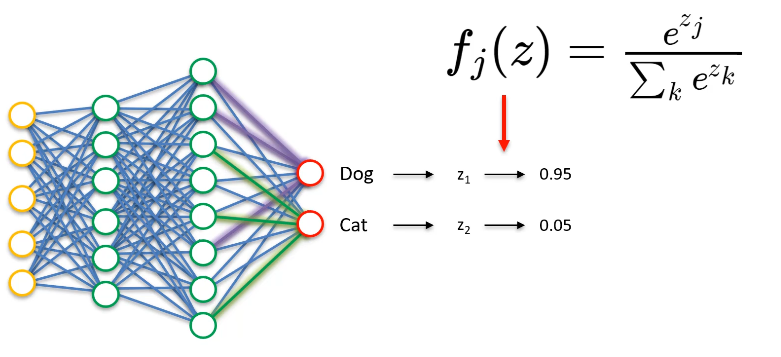
• Softmax : pour chaque neurone de sortie, on aura une valeur z qui représente la qualité de l'action correspondante. On applique ensuite une fonction exponentielle à chacune de ces valeurs, et on normalise le résultat pour avoir une somme égale à 1. Cela nous donne une probabilité pour chaque action possible. On choisit alors une action au hasard, en suivant ces probabilités. Cette stratégie est intéressante car elle permet de choisir des actions de manière moins déterministe que les stratégies précédentes, tout en gardant une certaine cohérence.

On a donc le concept d'exploration contre exploitation, c'est à dire de savoir lequel de ces deux conceptes nous devons utiliser le plus souvent. Prenons un exemple :

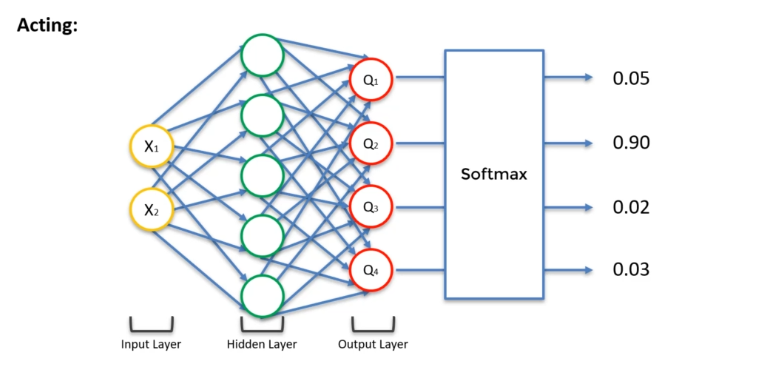
La réponse ici ne dit pas que Q2 sera obligatoirement la bonne valeur, mais qu'il y a 90 % de chances que ce soit la bonne. Q1 pourrait également être la bonne valeur. En clair, chaque action a un pourcentage de chances d'être choisie. Ainsi, il y a un juste milieu entre l'exploration et l'exploitation. Au début, il faut faire beaucoup d'exploration pour déterminer la valeur de Q la plus probable.

Trace d'éligibilité

La trace d'éligibilité est une méthode d'apprentissage en renforcement qui permet de mesurer la contribution de chaque action dans l'obtention d'une récompense. Elle est utilisée pour optimiser l'apprentissage et la prise de décision du système en renforcement.

La trace d'éligibilité est calculée en attribuant à chaque étape ou action une valeur d'éligibilité, qui représente la contribution de cette action à l'obtention de la récompense. Cette valeur est mise à jour à chaque étape en fonction de l'importance de l'action dans l'obtention de la récompense.

La trace d'éligibilité permet de prendre en compte l'historique des actions et des récompenses pour optimiser la prise de décision. Elle permet de pondérer les actions en fonction de leur importance dans l'obtention de la récompense et de favoriser les actions qui ont le plus contribué à l'obtention de la récompense.

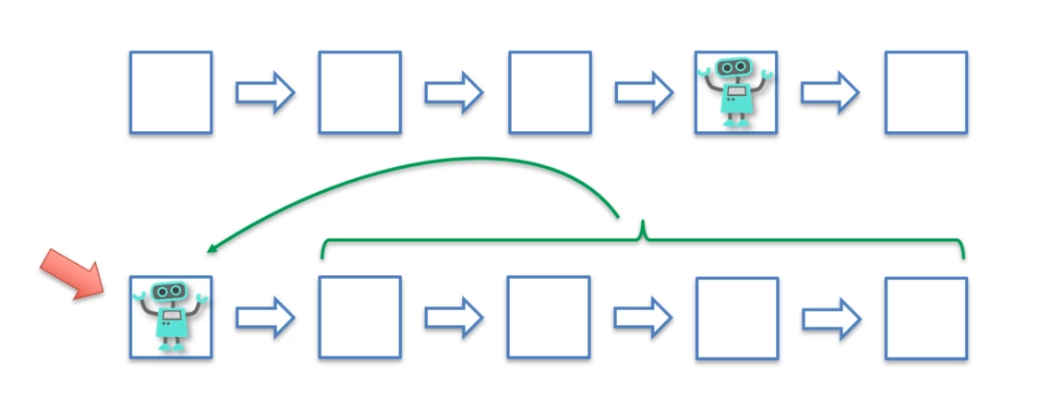
Dans le premier cas, le robot se déplace de case en case en se basant sur les récompenses qu'il obtient à chaque étape. Dans le deuxième cas, le robot teste différentes combinaisons de cases et évalue si elles sont bénéfiques ou non.

Dans le premier cas, le robot se contente d'acquérir des récompenses au fur et à mesure sans prendre assez de recul pour optimiser ses choix. Dans le deuxième cas, le robot analyse les combinaisons d'étapes qui ont bien fonctionné, mais aussi celles qui ont mal fonctionné afin de corriger ses choix pour atteindre la meilleure étape possible. Cette analyse est rendue possible grâce à la trace d'éligibilité qui permet de retracer les étapes qui ont conduit à la récompense obtenue. Ainsi, le robot peut facilement corriger ses erreurs et trouver la meilleure étape.

A3C : acteur-critique asynchrone avec avantage

L'A3C (Asynchronous Advantage Actor-Critic) est l'un des algorithmes les plus puissants dans le domaine de l'intelligence artificielle. Il s'agit d'un algorithme d'apprentissage par renforcement développé par Google en 2016. Il est plus efficace que les algorithmes précédemment utilisés et permet une phase d'apprentissage plus rapide.

L'A3C combine plusieurs techniques d'apprentissage par renforcement, notamment l'acteur-critique et l'avantage asynchrone.

Acteur critique

Changeons notre représentation du réseau de neurones :

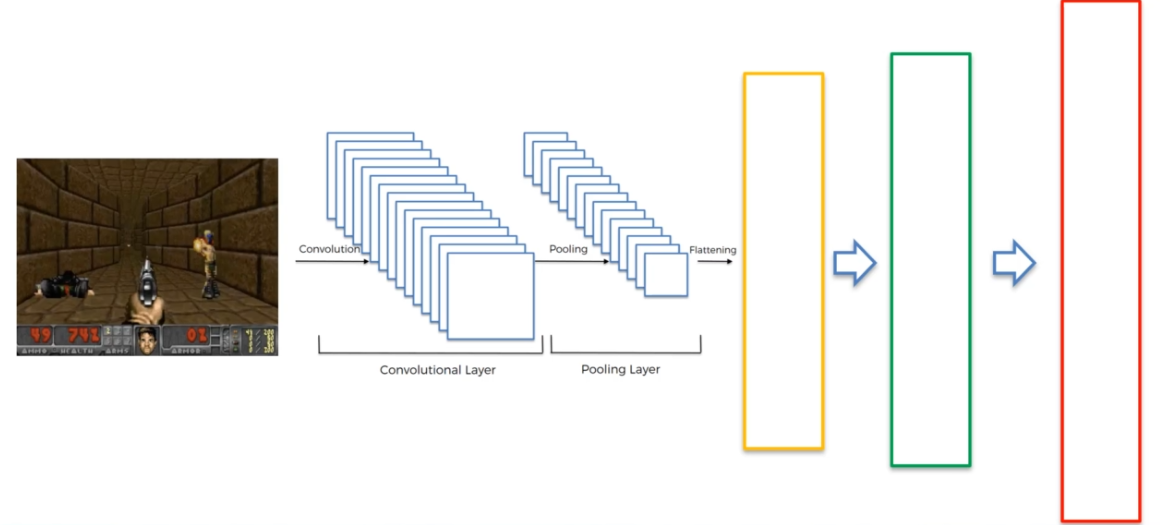
Dans l'algorithme Acteur critique, la partie fondamentale consiste à ajouter une deuxième sortie. La première sortie est la représentation des valeurs Q, qui est gérée par l'acteur. La deuxième sortie est la valeur de V, qui représente la valeur d'un état particulier et qui est gérée par le critique.

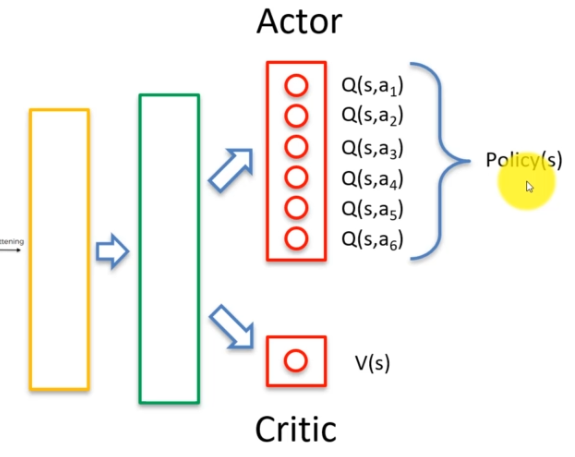
Le rôle de l'acteur est de choisir les actions à effectuer, tandis que le rôle du critique est d'évaluer la qualité de ces actions. En combinant les deux sorties, l'algorithme Acteur critique peut à la fois apprendre à choisir les meilleures actions possibles et évaluer la qualité de ces actions en temps réel.

L'algorithme Actor-Critic est couramment utilisé en apprentissage par renforcement et a permis de résoudre de nombreux problèmes complexes en intelligence artificielle. En combinant les avantages de l'acteur et du critique, il permet d'obtenir une meilleure performance d'apprentissage et une prise de décision plus efficace.

Asynchrone

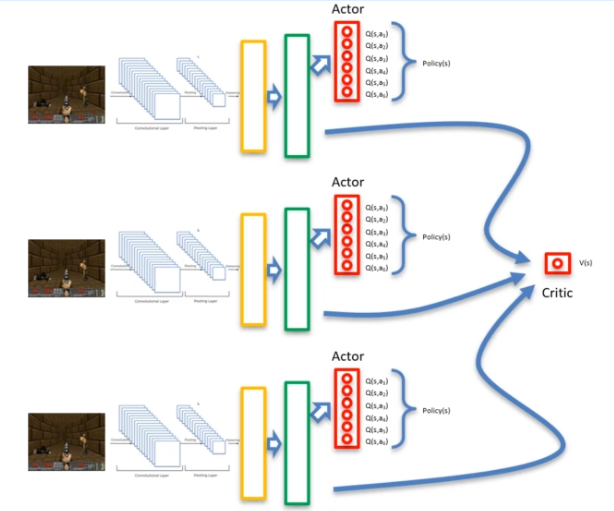
Au lieu d'utiliser un seul agent, la méthode consiste à utiliser deux agents qui partent d'un point différent. Cela permet d'augmenter le nombre d'explorations et de réduire les risques qu'un agent se bloque. Les agents peuvent alors apprendre les uns des autres grâce à leurs explorations et partager la valeur critique. Cette valeur V est associée à un réseau de neurones partagé, qui est mis à la disposition des réseaux de neurones des agents.

Ainsi, en utilisant cette méthode, nous avons N agents, chacun avec leur propre réseau de neurones, ainsi qu'un réseau de neurones partagé. Cette approche permet d'optimiser l'apprentissage en renforcement et d'obtenir de meilleures performances en utilisant la collaboration entre agents.

Avantage

Lorsque la fonction V apparaît dans l'algorithme, il est nécessaire de lui donner une notion de coût. C'est là qu'intervient la valeur de Policy Loss, qui permet de quantifier à quel point une action est bonne ou non.

Tout d'abord, il convient de rappeler la formule de l'avantage : A = Q(s,a) - V(s). Ensuite, on peut expliquer les valeurs de coûts :

Value Loss : Cette fonction de coût permet de comparer la valeur Q estimée à la valeur Q obtenue en appliquant la méthode de Bellman.

Policy Loss : Cette fonction de coût permet de quantifier à quel point une action est bonne ou non. Si la valeur Q est supérieure à 2, cela signifie que l'action choisie est meilleure que prévu. À l'inverse, si la valeur Q est inférieure à 1, cela signifie que l'action choisie n'est pas bonne.

Ces fonctions de coût sont ensuite rétropropagées dans les réseaux de neurones pour améliorer la valeur critique de V ainsi que la valeur de s et a, afin de maximiser l'avantage de l'équation. Cela permet d'optimiser la prise de décision et d'améliorer les performances de l'algorithme en renforcement.

Large Mémoire Court-Terme (LSTM)

Une modification importante a été apportée au niveau de la couche cachée en ajoutant une couche LSTM. Cette couche permet au réseau de neurones de disposer d'une mémoire, lui permettant ainsi de se souvenir de ce qui s'est passé précédemment. Lorsque l'on donne une image en entrée au réseau, il peut maintenant se rappeler des événements passés ainsi que des souvenirs des états précédents.

En utilisant une couche LSTM, le réseau de neurones peut améliorer ses performances en apprentissage par renforcement en prenant en compte l'historique des états précédents. Cela permet au réseau de neurones de mieux comprendre les enchaînements d'actions et de prendre des décisions plus efficaces en fonction des événements passés. La mémoire à long terme permet ainsi au réseau de neurones de mieux modéliser le contexte et d'améliorer sa capacité à prendre des décisions précises en fonction de la situation actuelle.

Comment cela fonctionne ? ![][https://res.cloudinary.com/dw6srr9v6/image/upload/v1636693594/lstms_eaf9a1baa5.png)

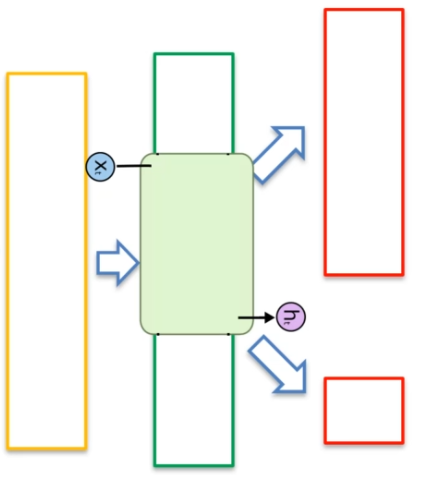
Dans un réseau de neurones LSTM, nous avons une entrée Xt qui correspond à la couche précédente et une sortie Ht qui correspond à la couche suivante (flèche vers le haut du schéma). En plus de ces entrées et sorties, nous avons deux autres entrées :

• Ht-1 : Cette entrée permet au réseau de neurones de se souvenir de l'étape précédente et d'apprendre de cette étape. C'est une valeur qui est réutilisée pour l'étape suivante.
• Ct-1 : Cette entrée correspond à la mémoire de l'étape précédente. Il s'agit d'une information persistante qui permet au réseau de neurones de se souvenir des événements passés.

Le réseau de neurones LSTM dispose également de deux sorties :

• Ct : Cette sortie correspond à la mémoire de sortie. Elle permet au réseau de neurones de stocker des informations pour une utilisation ultérieure.
• Ht : Cette sortie est réutilisée pour l'étape suivante du réseau de neurones. Elle permet au réseau de neurones de se souvenir de l'état précédent et d'utiliser ces informations pour prendre des décisions plus précises en fonction du contexte actuel.

En utilisant ces entrées et sorties, le réseau de neurones LSTM peut améliorer sa capacité à prendre en compte l'historique des événements passés et à prendre des décisions plus précises en fonction du contexte actuel.