Surapprentissage et sous-apprentissage

Qu'est-ce que c'est ?

L'apprentissage automatique est un outil puissant qui peut être utilisé pour faire des prévisions et des décisions basées sur des données. Cependant, comme pour tout outil, il est important de l'utiliser correctement pour obtenir les meilleurs résultats. Dans cet article, nous allons explorer deux problèmes courants qui peuvent survenir lors de l'utilisation d'algorithmes d'apprentissage automatique : le surapprentissage et le sous-apprentissage.

Le surapprentissage et le sous-apprentissage

Tout d'abord, regardons le surapprentissage. Le surapprentissage se produit lorsqu'un modèle est trop complexe pour les données qu'il essaie de s'adapter. Cela peut se produire lorsqu'il y a trop de caractéristiques ou lorsque le modèle est trop flexible. Le résultat est que le modèle s'adapte parfaitement aux données d'entraînement, mais se comporte mal sur de nouvelles données.

Pour illustrer ce concept, considérons un exemple de prédiction des prix de l'immobilier avec la régression linéaire. Supposons que nos données ressemblent à cela:

Taille de la maison (x)	Prix (y))
1000	200,000
1200	250,000
1400	300,000
1600	350,000
1800	400,000

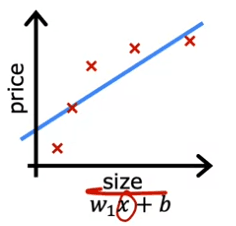
Une chose que nous pourrions faire est d'ajuster une fonction linéaire à ces données. Si nous faisons cela, nous obtenons une courbe droite qui ressemble à cela :

y = 200 000 + 0,2x

Mais ce n'est pas un très bon modèle. En regardant les données, il semble évident que lorsque la taille de la maison augmente, le prix de l'immobilier s'aplatit. Cet algorithme ne s'adapte pas très bien aux données d'entraînement. Le terme technique pour cela est que le modèle sous-ajuste les données d'entraînement. Un autre terme est que l'algorithme a une forte biais.

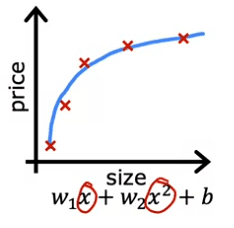
Maintenant, regardons une deuxième variation de modèle, qui est si nous insérons une fonction quadratique dans les données avec deux caractéristiques, x et x^2. Ensuite, lorsque nous ajustons les paramètres W1 et W2, nous pouvons obtenir une courbe qui s'adapte aux données un peu mieux. Peut-être que cela ressemble à ceci :

y = 200 000 + 0,2x + 0,001x^2

De plus, si nous avions une nouvelle maison qui n'est pas dans cet ensemble de cinq exemples d'entraînement, ce modèle ferait probablement bien sur cette nouvelle maison. Si vous êtes des agents immobiliers, l'idée que vous voulez que votre algorithme d'apprentissage fonctionne bien, même sur des exemples qui ne sont pas sur l'ensemble d'entraînement, cela s'appelle la généralisation. Techniquement, nous disons que vous voulez que votre algorithme d'apprentissage généralise bien, ce qui signifie faire de bonnes prévisions même sur de nouveaux exemples qu'il n'a jamais vus auparavant. Ces modèles quadratiques semblent s'adapter à l'ensemble d'entraînement pas parfaitement, mais assez bien.

Maintenant, regardons l'autre extrême. Que se passerait-il si nous devions adapter un polynôme de quatrième degré aux données? Vous avez x, x^2, x^3 et x^4 comme caractéristiques. Avec ce polynôme de quatrième degré, nous pouvons en fait adapter la courbe qui passe à travers les cinq exemples d'entraînement. Mais ceci est clairement en sur-apprentissage des données. Ce modèle est trop complexe et flexible pour les données et il est susceptible de se comporter mal sur de nouvelles données.

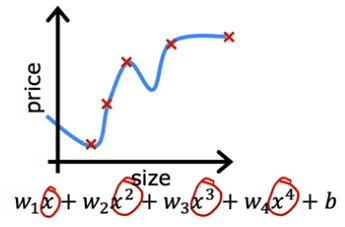
Pour éviter le surapprentissage, nous pouvons utiliser des techniques telles que la régularisation. La régularisation est une technique qui nous aide à minimiser le problème de surapprentissage et à améliorer les performances de nos algorithmes d'apprentissage.

Il est important de garder à l'esprit que le surapprentissage et le sous-apprentissage ne sont pas toujours faciles à reconnaître et qu'il peut parfois être nécessaire de faire des expérimentations pour trouver le bon équilibre entre le surapprentissage et le sous-apprentissage. C'est pourquoi il est important également de vérifier les performances du modèle sur l'ensemble de test, qui n'est pas utilisé pour l'entraînement, pour voir comment le modèle généralise à de nouveaux exemples non vus.

Example

Importons nos différentes dépendances. Ici, nous utilisons une librairie que vous pouvez retrouver sur le github

 import matplotlib.pyplot as plt
from ipywidgets import Output
from plt_overfit import overfit_example, output

plt.close("all")
display(output)
ofit = overfit_example(False)

Le graphique suivant devrait s'afficher:

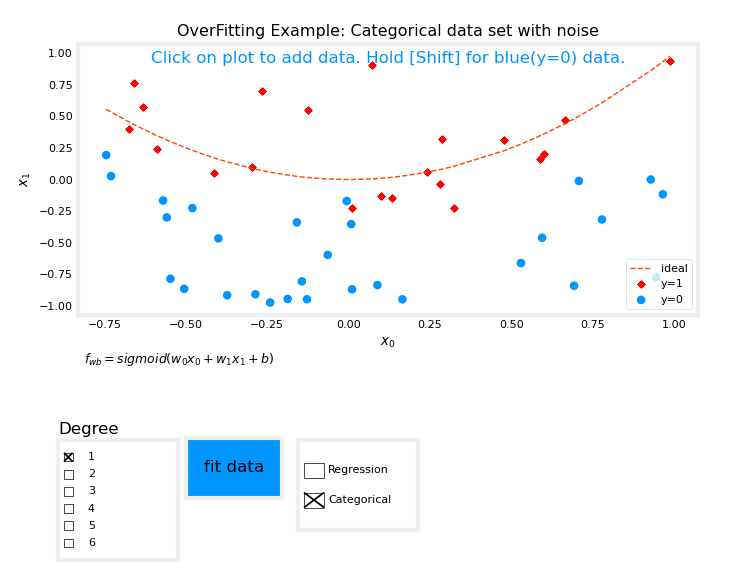
Le graphique ci-dessus vous permet de basculer entre les exemples de régression et de catégorisation, d'ajouter des données, de sélectionner le degré du modèle et d'ajuster le modèle aux données.

Vous devriez essayer d'ajuster les données avec un degré = 1 et de noter le "sous-entrainement", d'ajuster les données avec un degré = 6 et de noter le "surentrainement" et de régler le degré pour obtenir le "meilleur apprentissage".

L'ajout de données telles que des exemples extrêmes peut augmenter le surentrainement, tandis que des exemples nominaux peuvent le réduire. Les courbes "idéales" représentent le modèle générateur auquel du bruit a été ajouté pour créer l'ensemble de données, et la fonction "ajustement" utilise une méthode autre que la descente de gradient pure pour une vitesse améliorée et peut être utilisée sur des jeux de données plus petits.

Comment le traiter ?

Le surapprentissage est un problème courant lorsque l'on travaille avec des algorithmes d'apprentissage automatique. Il se produit lorsqu'un modèle est trop bien formé sur les données d'entraînement et, en conséquence, il se comporte mal sur les nouvelles données non vues. Dans cet article, nous discuterons des moyens de traiter le surapprentissage et de rendre votre modèle plus robuste.

Collecter plus de données d'entraînement

Une façon de traiter le surapprentissage consiste à collecter plus de données d'entraînement. Plus le nombre d'exemples d'entraînement augmente, plus l'algorithme d'apprentissage apprendra à adapter une fonction qui est moins sinueuse et donc moins sujette au surapprentissage. Par exemple, si nous essayons de prévoir les prix des maisons et que nous avons un nombre limité de points de données, nous pouvons rassembler plus de données sur les tailles et les prix des maisons pour rendre notre modèle plus robuste. Cependant, obtenir plus de données peut ne pas être toujours une option, et dans de tels cas, nous pouvons explorer d'autres options.

Utiliser moins de caractéristiques

Un autre moyen de traiter le surapprentissage consiste à utiliser moins de caractéristiques. Dans certains cas, le surapprentissage peut se produire lorsqu'il y a trop de caractéristiques et pas assez de données. Dans de tels cas, nous pouvons sélectionner un sous-ensemble des caractéristiques les plus utiles et utiliser seulement cela pour entraîner notre modèle. Ce processus est connu sous le nom de sélection de caractéristiques. Il est important de noter que la sélection de caractéristiques peut entraîner la suppression de certaines des informations que vous avez sur les maisons.

Régularisation

La troisième option pour réduire le surapprentissage est la régularisation. La régularisation est une technique qui encourage l'algorithme d'apprentissage à réduire les valeurs des paramètres sans nécessairement les éliminer. Cela rend le modèle moins complexe et moins sujet au surapprentissage. Dans la prochaine section, nous discuterons de la régularisation en détail et verrons comment elle peut être utilisée pour améliorer nos modèles.

En résumé, le surapprentissage est un problème courant lorsque l'on travaille avec des algorithmes d'apprentissage automatique, et il peut être traité en collectant plus de données, en utilisant moins de caractéristiques ou en utilisant une régularisation. Chacune de ces options a ses propres avantages et inconvénients, et il est essentiel de choisir celle qui convient le mieux à votre problème. Dans les cours ultérieurs, nous discuterons également de techniques plus avancées pour traiter le surapprentissage, telles que la validation croisée et l'arrêt prématuré.

Comment cela marche avec la fonction de coût ?

La régularisation est une technique utilisée pour lutter contre le surapprentissage dans les algorithmes d'apprentissage automatique. Elle consiste à ajouter un terme de pénalité à la fonction coût, ce qui incite le modèle à avoir des valeurs de paramètres plus petites. Dans cet article, nous allons discuter de la manière dont la régularisation peut être appliquée à votre algorithme d'apprentissage pour rendre votre modèle plus robuste.

Tout d'abord, rappelons un exemple de la section précédente, dans laquelle nous avons vu qu'en ajustant une fonction quadratique aux données, cela donne un bon ajustement. Mais si vous ajustez une fonction polynomiale très élevée, vous obtenez une courbe qui surapprend les données. Pour résoudre ce problème, nous pouvons modifier la fonction coût et ajouter un terme qui pénalise le modèle si les paramètres W3 et W4 sont importants. Par exemple, nous pouvons ajouter 1000 fois W3 carré plus 1000 fois W4 carré à la fonction coût. Cette fonction coût modifiée incitera le modèle à avoir des valeurs plus petites pour W3 et W4, ce qui est équivalent à avoir un modèle plus simple avec moins de caractéristiques et donc moins sujet au surapprentissage.

L'idée derrière la régularisation est de pénaliser tous les paramètres Wj, au lieu de seulement W3 et W4. De cette façon, nous n'avons pas besoin de savoir quelles caractéristiques sont les plus importantes et nous pouvons utiliser toutes les caractéristiques sans s'inquiéter de surapprendre. Par exemple, si nous avons des données avec 100 caractéristiques pour chaque maison, il peut être difficile de choisir les caractéristiques à inclure et lesquelles à exclure. Donc, construisons un modèle qui utilise toutes les 100 caractéristiques et pénalisons-les toutes en ajoutant un nouveau terme lambda fois la somme de wj carré. Cette valeur lambda est appelée le paramètre de régularisation et doit être choisie avec soin.

En conclusion, la régularisation est une technique qui peut être utilisée pour lutter contre le surapprentissage dans les algorithmes d'apprentissage automatique. Elle fonctionne en ajoutant un terme de pénalité à la fonction coût, ce qui incite le modèle à avoir des valeurs de paramètres plus petites. En convention, le terme de régularisation est divisé par 2m, ce qui facilite le choix d'une bonne valeur pour lambda, et il est également indépendant de l'échelle, ce qui signifie que la même valeur de lambda peut être utilisée indépendamment de la taille de l'ensemble d'entraînement. Dans les cours ultérieurs, nous discuterons également des techniques plus avancées de régularisation, telles que la régularisation L1 et L2.

Linear regression régulée

La régression linéaire est une méthode couramment utilisée pour modéliser la relation entre une variable dépendante et une ou plusieurs variables indépendantes. Cependant, dans certains cas, le modèle peut devenir trop ajusté, ce qui signifie qu'il s'adapte trop bien aux données d'entraînement et qu'il ne peut pas bien fonctionner sur de nouvelles données. Pour éviter cela, nous pouvons ajouter un terme de régularisation à la fonction de coût.

La fonction de coût pour la régression linéaire régularisée est une combinaison de la fonction de coût d'erreur carrée habituelle et d'un terme de régularisation supplémentaire. Le terme de régularisation est contrôlé par un paramètre, Lambda, et l'objectif est de trouver les paramètres w et b qui minimisent la fonction de coût régularisée.

Nous pouvons définir notre fonction comme :

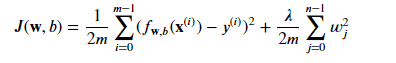
Où: 𝑓𝐰,𝑏(𝐱(𝑖))=𝐰⋅𝐱(𝑖)+𝑏

Nous pouvons alors implémenter cet fonction comme :

 def compute_cost_linear_reg(X, y, w, b, lambda_ = 1):
    """
    Computes the cost over all examples
    """

    m  = X.shape[0]
    n  = len(w)
    cost = 0.
    for i in range(m):
        f_wb_i = np.dot(X[i], w) + b                               
        cost = cost + (f_wb_i - y[i])**2                               
    cost = cost / (2 * m)                                             
 
    reg_cost = 0
    for j in range(n):
        reg_cost += (w[j]**2)                                          
    reg_cost = (lambda_/(2*m)) * reg_cost                            
    
    total_cost = cost + reg_cost                                   
    return total_cost

Auparavant, nous avons utilisé la descente de gradient pour la fonction de coût originale. Cependant, maintenant que nous avons ajouté le terme de régularisation, les mises à jour pour les paramètres w et b sont légèrement différentes. La mise à jour pour w est donnée par la formule suivante : w_j = w_j * (1 - Alpha * Lambda / m) - Alpha * (1/m) * term

où Alpha est un petit nombre positif appelé taux d'apprentissage, m est la taille de l'ensemble d'entraînement et term est une expression spécifique pour la dérivée de la fonction de coût par rapport à w_j. La mise à jour pour b reste la même qu'avant.

Il est important de noter que le terme de régularisation n'affecte que la mise à jour pour w, pas b. C'est parce que l'objectif de la régularisation est de réduire les paramètres, et dans ce cas, nous essayons de réduire les paramètres w, mais pas b.

Pour mettre en œuvre la descente de gradient pour la régression linéaire régularisée, les mises à jour pour w et b doivent être effectuées simultanément. La mise à jour pour w doit être effectuée pour toutes les valeurs de j de 1 à n, et la mise à jour pour b doit être effectuée selon la formule précédente.

Nous pouvons définir notre fonction comme :

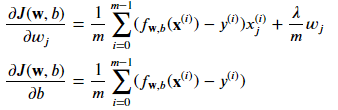
Nous pouvons alors implémenter cet fonction comme :

 def compute_gradient_linear_reg(X, y, w, b, lambda_): 
    """
    Computes the gradient for linear regression 
    """
    m,n = X.shape           #(number of examples, number of features)
    dj_dw = np.zeros((n,))
    dj_db = 0.

    for i in range(m):                             
        err = (np.dot(X[i], w) + b) - y[i]                 
        for j in range(n):                         
            dj_dw[j] = dj_dw[j] + err * X[i, j]               
        dj_db = dj_db + err                        
    dj_dw = dj_dw / m                                
    dj_db = dj_db / m   
    
    for j in range(n):
        dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]

En résumé, la régression linéaire régularisée est une méthode pour éviter le surajustement dans les modèles de régression linéaire. Il est mis en œuvre en ajoutant un terme de régularisation à la fonction de coût et en mettant à jour les paramètres à l'aide de la descente de gradient. Les mises à jour pour les paramètres sont légèrement différentes de celles d'avant, le terme de régularisation n'affectant que les mises à jour pour w, pas b. Cela nous permet de réduire les paramètres w pour améliorer les performances du modèle sur de nouvelles données.

Logistic regression régulée

Dans cette section, nous allons discuter de la régression logistique régularisée et de la manière de l'implémenter en utilisant la descente de gradient. La régression logistique est une méthode couramment utilisée pour modéliser la relation entre une variable dépendante et une ou plusieurs variables indépendantes dans les problèmes de classification. Cependant, dans certains cas, le modèle peut devenir surajusté, ce qui signifie qu'il s'adapte trop bien aux données d'entraînement et peut ne pas fonctionner bien sur de nouvelles données. Pour éviter le surajustement, nous pouvons ajouter un terme de régularisation à la fonction de coût.

La fonction de coût pour la régression logistique régularisée est une combinaison de la fonction de coût habituelle de la régression logistique et d'un terme de régularisation supplémentaire. Le terme de régularisation est contrôlé par un paramètre, Lambda, et l'objectif est de trouver les paramètres w et b qui minimisent la fonction de coût régularisée.

Nous pouvons définir notre fonction comme :

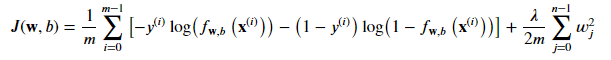
Où: 𝑓𝐰,𝑏(𝐱(𝑖))=𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝐰⋅𝐱(𝑖)+𝑏)

We can imagine to implement it like this :

 def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):
    """
    Computes the cost 
    """

    m,n  = X.shape
    cost = 0.
    for i in range(m):
        z_i = np.dot(X[i], w) + b                                      
        f_wb_i = sigmoid(z_i)                                         
        cost +=  -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)      
             
    cost = cost/m                                                      

    reg_cost = 0
    for j in range(n):
        reg_cost += (w[j]**2)                                          
    reg_cost = (lambda_/(2*m)) * reg_cost                              
    
    total_cost = cost + reg_cost                                       
    return total_cost

Tout comme la régression linéaire régularisée, la mise à jour de la descente de gradient pour la régression logistique régularisée ressemblera également. La mise à jour pour w est donnée par la formule suivante :

*w_j = w_j - Alpha * (1/m) * (term + (Lambda/m)w_j)

paramètres w pour améliorer les performances du modèle sur de nouvelles données.

Il est important de noter que le terme de régularisation n'affecte que la mise à jour de w, pas b. Cela est dû au fait que l'objectif de la régularisation est de réduire les paramètres, et dans ce cas, nous essayons de réduire les paramètres w, mais pas b.

Pour implémenter la descente de gradient pour la régression logistique régularisée, les mises à jour de w et b doivent être effectuées simultanément. La mise à jour de w doit être effectuée pour toutes les valeurs de j de 1 à n, et la mise à jour de b doit être effectuée selon la formule précédente.

Nous pouvons définir notre fonction comme :

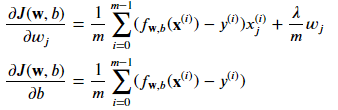
Nous pouvons alors implémenter cet fonction comme :

 def compute_gradient_logistic_reg(X, y, w, b, lambda_): 
    """
    Computes the gradient for linear regression 
    """
    m,n = X.shape
    dj_dw = np.zeros((n,))                            #(n,)
    dj_db = 0.0                                       #scalar

    for i in range(m):
        f_wb_i = sigmoid(np.dot(X[i],w) + b)          #(n,)(n,)=scalar
        err_i  = f_wb_i  - y[i]                       #scalar
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err_i * X[i,j]      #scalar
        dj_db = dj_db + err_i
    dj_dw = dj_dw/m                                   #(n,)
    dj_db = dj_db/m                                   #scalar

    for j in range(n):
        dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]

    return dj_db, dj_dw

En résumé, la régression logistique régularisée est une méthode pour éviter le surajustement dans les modèles de régression logistique. Il est implémenté en ajoutant un terme de régularisation à la fonction de coût et en mettant à jour les paramètres à l'aide de la descente de gradient. Les mises à jour des paramètres sont similaires à la régression linéaire régularisée, avec le terme de régularisation n'affectant que les mises à jour de w, pas b. Cela nous permet de réduire les paramètres w pour améliorer les performances du modèle sur de nouvelles données.

En comprenant et en étant capable d'appliquer la régression logistique régularisée, vous aurez la capacité de créer des applications précieuses dans le domaine de l'apprentissage automatique. Bien que les résultats d'apprentissage spécifiques soient importants, savoir quand et comment réduire le surajustement s'avère être l'une des compétences très importantes dans le monde réel aussi.

J'espère que vous avez apprécié cet article et avez acquis une compréhension plus profonde de la régression logistique régularisée et de la manière de l'implémenter en utilisant la descente de gradient.