Introduction

Lorsque les réseaux de neurones ont été inventés pour la première fois, le but était de créer un logiciel qui pourrait imiter la façon dont le cerveau humain apprend et pense. Bien que les réseaux de neurones d'aujourd'hui soient considérablement différents du cerveau biologique, les motivations originales jouent encore un rôle important dans la façon dont nous les considérons.

Le cerveau humain est considéré comme la forme la plus avancée d'intelligence, et les réseaux de neurones ont été créés dans le but de construire un logiciel qui pourrait en imiter le fonctionnement. Les travaux sur les réseaux de neurones ont commencé dans les années 1950, mais ils sont tombés en désuétude pendant un certain temps. Dans les années 1980 et au début des années 1990, ils ont retrouvé leur popularité et ont montré des résultats prometteurs dans des applications telles que la reconnaissance de chiffres manuscrits. Cependant, ils sont tombés à nouveau en désuétude à la fin des années 1990.

Ce n'est qu'en 2005 que les réseaux de neurones ont connu un regain d'intérêt et ont été rebaptisés "apprentissage profond". Le terme "apprentissage profond" a pris de l'ampleur car il sonne plus impressionnant que "réseaux de neurones". Depuis lors, les réseaux de neurones ont été utilisés dans une grande variété de domaines d'application, notamment la reconnaissance de la parole, la vision par ordinateur, le traitement du langage naturel, et bien plus encore.

Bien que les réseaux de neurones modernes n'aient presque rien à voir avec la façon dont le cerveau apprend réellement, la motivation initiale de tenter de l'imiter reste importante. Pour comprendre comment fonctionne le cerveau, il est important de comprendre la structure des neurones. Les neurones sont les blocs de construction de base du cerveau et sont responsables de l'envoi d'impulsions électriques qui composent la pensée humaine.

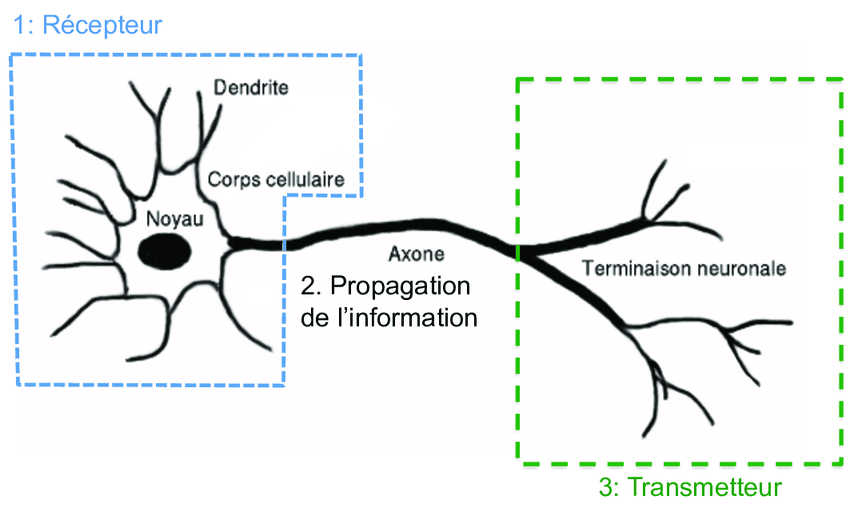
Un diagramme simplifié d'un neurone biologique montre qu'il comprend un corps cellulaire, des entrées (appelées dendrites) et des sorties (appelées axones). Le neurone reçoit des impulsions électriques provenant d'autres neurones à travers ses dendrites, les traite et envoie des impulsions de sortie à d'autres neurones à travers ses axones. Ce processus est répété encore et encore, avec la sortie d'un neurone devenant l'entrée d'un autre, et ainsi de suite.

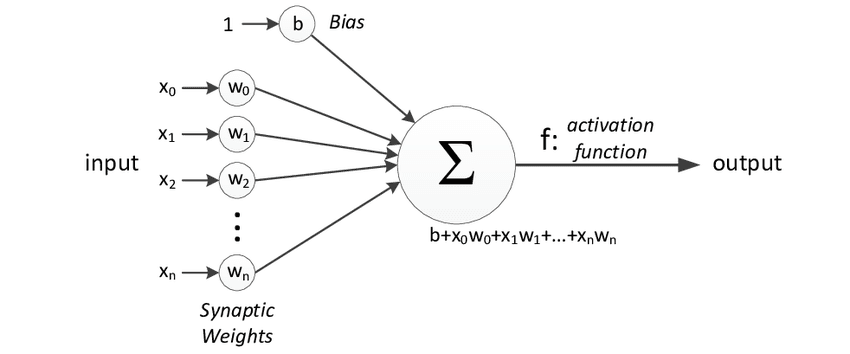
Lors de la construction d'un réseau de neurones artificiel ou d'un algorithme d'apprentissage profond, le bloc de construction de base est le neurone. Un neurone prend un ou plusieurs entrées, qui sont simplement des nombres, effectue une certaine computation et produit un autre nombre. Ces sorties peuvent ensuite être utilisées comme entrées pour d'autres neurones. De cette façon, de nombreux neurones peuvent être simulés en même temps pour créer un réseau.

Dans ce diagramme, trois neurones sont montrés travaillant ensemble. Ils prennent quelques nombres en entrée, effectuent une computation et produisent d'autres nombres en sortie. Cependant, il est important de noter qu'il existe une analogie imparfaite entre les neurones biologiques et les neurones artificiels, et que nous avons actuellement une compréhension limitée de la façon dont le cerveau humain fonctionne réellement.

En résumé, les réseaux de neurones ont été créés dans le but de mimer la façon dont le cerveau humain apprend et pense. Bien que la technologie ait beaucoup évolué depuis sa création, les motivations originales restent un élément important de la façon dont nous pensons aux réseaux de neurones aujourd'hui.

Demande de prediction

Lors de la construction d'un réseau neuronal, il est important de comprendre le bloc de base : le neurone. Un neurone prend un ou plusieurs entrées, qui sont simplement des nombres, effectue une computation et produit une autre sortie. Ces sorties peuvent ensuite être utilisées en tant qu'entrées pour d'autres neurones. De cette manière, de nombreux neurones peuvent être simulés en même temps pour créer un réseau.

• Pour illustrer ce concept, prenons un exemple de prédiction de la demande pour les T-shirts.
• L'objectif est de prédire si un T-shirt sera un best-seller ou non, en se basant sur des données telles que le prix du T-shirt et s'il est devenu ou non un best-seller par le passé.

Ce type d'application est utilisé par les détaillants pour planifier de meilleurs niveaux d'inventaire et des campagnes publicitaires.

Dans cet exemple, la caractéristique d'entrée x est le prix du T-shirt et l'objectif est de prédire si un T-shirt particulier sera un best-seller ou non. Pour ce faire, nous utilisons la régression logistique pour ajuster une fonction sigmoïde aux données. La sortie de la prédiction est représentée par la formule : f(x) = 1/1 + e^(-wx + b) où w et b sont des paramètres appris lors de la formation du modèle.

Cette sortie, que nous notons a, représente la probabilité que le T-shirt soit un best-seller. Autre manière de le considérer est que cette unité de régression logistique peut être considérée comme un modèle simplifié d'un neurone unique dans le cerveau. Il prend en entrée la caractéristique, le prix, et calcule la sortie, la probabilité que le T-shirt soit un best-seller.

Pour créer un réseau neuronal, nous prenons un certain nombre de ces unités de régression logistique et les connectons ensemble pour faire une prédiction finale.

Dans cet exemple, nous avons 4 caractéristiques pour prédire si un T-shirt sera un best-seller ou non. Les caractéristiques sont :

• Le prix du T-shirt
• Les coûts d'expédition
• Les montants de la publicité d'un T-shirt particulier
• La qualité du matériau, est-ce un coton de haute qualité épais ou peut-être un matériau de qualité inférieure ?

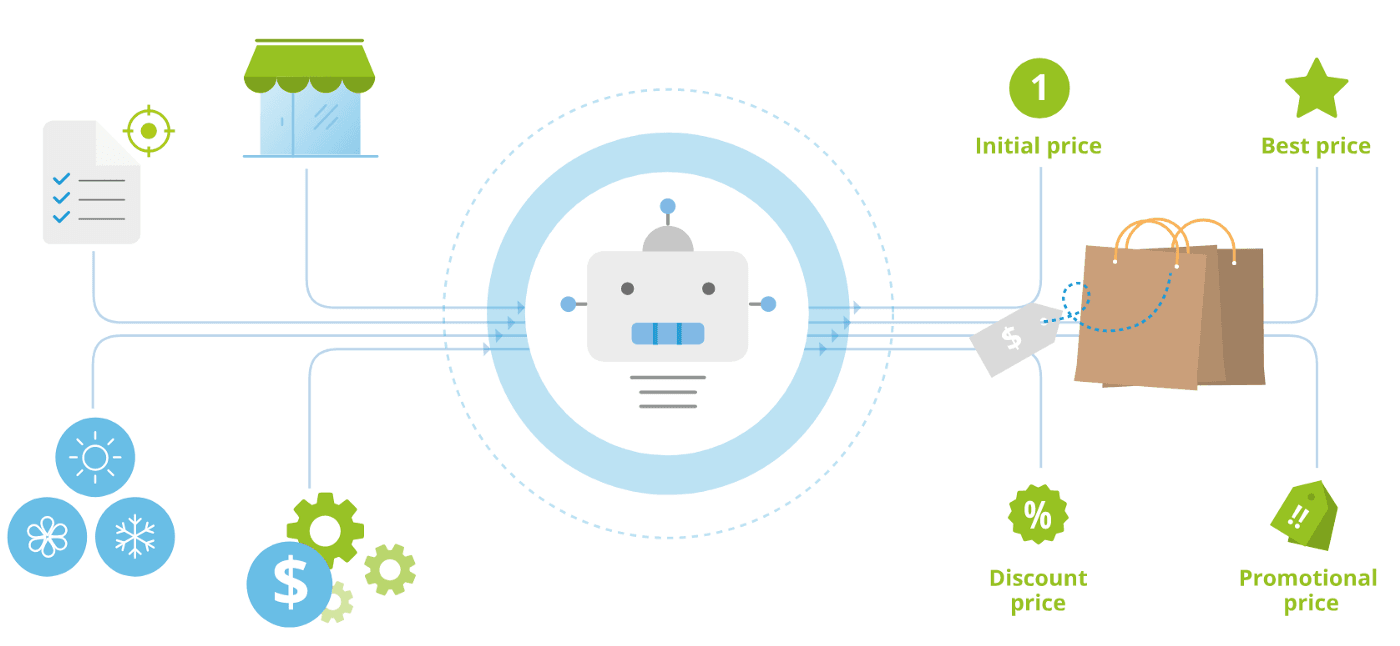
Chacune de ces caractéristiques est entrée dans une unité de régression logistique séparée, qui calcule la probabilité que le T-shirt soit abordable, ait une forte visibilité ou soit perçu comme de haute qualité. Ces probabilités sont ensuite combinées pour faire une prédiction finale de si le T-shirt sera un best-seller ou non.

chaque features est appelées, couche d'entrée et est représenté par un vecteurX (X->). Il existe des couches cachees, appelée vecteur (A->) ou activations, pour finir sur la couche de probalité A.

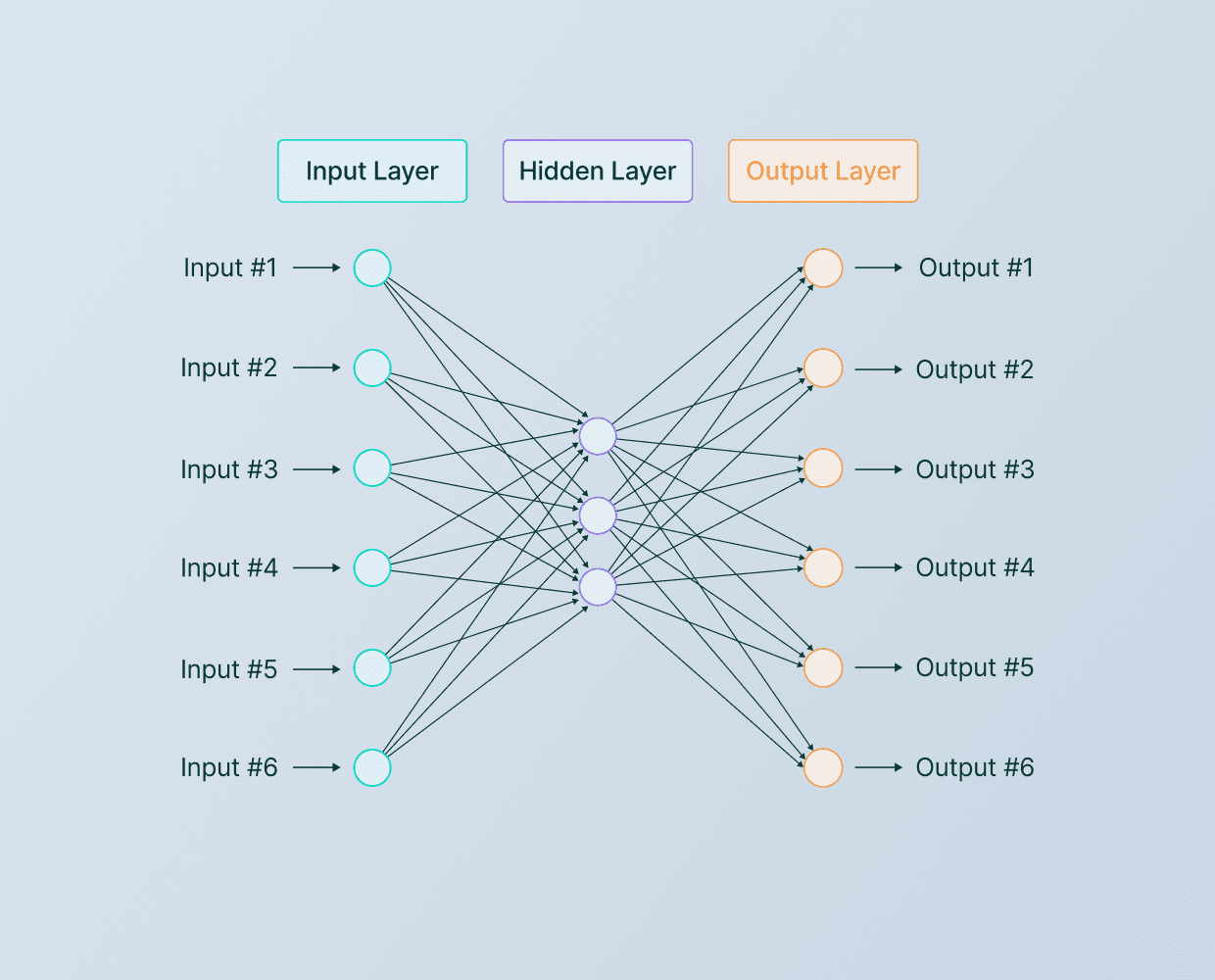
Il est important de noter que, bien que l'algorithme de régression logistique soit un modèle simplifié d'un seul neurone dans le cerveau, les algorithmes d'apprentissage profond fonctionnent très bien en pratique. Construire un réseau neuronal consiste à prendre un certain nombre de ces neurones et à les relier ensemble pour faire une prédiction.

Modèle d'un réseau de neurones

Les blocs de construction de la plupart des réseaux neuronaux sont des couches de neurones. Dans cet article, nous allons explorer comment construire une couche de neurones et comment utiliser ces blocs de construction pour créer un réseau neuronal plus grand.

Comme exemple, prenons un problème de prédiction de la demande où nous avons quatre caractéristiques d'entrée qui sont envoyées à une couche cachée avec trois neurones. Ces trois neurones envoient ensuite leur sortie à une couche de sortie avec un neurone.

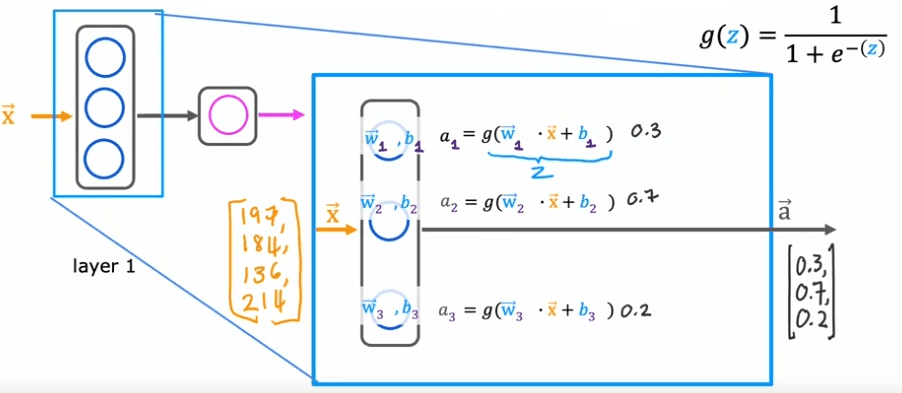
Pour comprendre comment fonctionne la couche cachée, examinons de plus près les calculs. La couche cachée prend en entrée quatre nombres, qui sont ensuite transmis à chacun des trois neurones. Chaque neurone est essentiellement une unité de régression logistique, avec ses propres paramètres (w et b). Par exemple, le premier neurone a les paramètres w_1 et b_1, et il produit une valeur d'activation a, qui est calculée comme g(w_1 * x + b_1), où g est la fonction logistique et x est l'entrée. Cette valeur d'activation, a_1, représente la probabilité que l'entrée soit très abordable.

De manière similaire, le deuxième neurone a les paramètres w_2 et b_2 et calcule une valeur d'activation a_2, qui représente la probabilité que les acheteurs potentiels connaissent le produit. Le troisième neurone a les paramètres w_3 et b_3 et calcule une valeur d'activation a_3. Le vecteur de ces trois valeurs d'activation, [a_1, a_2, a_3], est ensuite transmis à la couche de sortie finale du réseau neuronal.

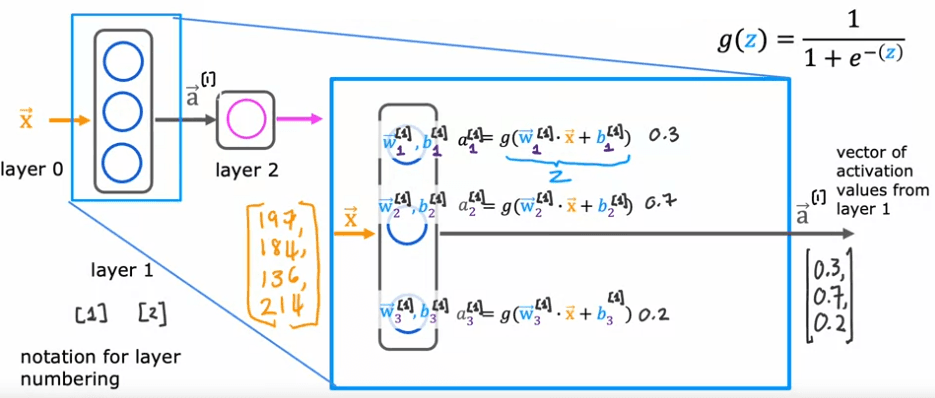
Lors de la construction de réseaux neuronaux à plusieurs couches, il est utile de donner des numéros différents aux couches. Par convention, la couche d'entrée est appelée couche 0, cette couche cachée est appelée couche 1 et la couche de sortie est appelée couche 2. Cependant, aujourd'hui les réseaux neuronaux peuvent avoir des dizaines voir même des centaines de couches. Pour suivre les différentes couches, nous pouvons utiliser des crochets carrés exponentiels pour indiquer à quelle couche nous nous référons. Par exemple, a¹ se réfère à la sortie de la couche 1, w²_1 se réfère aux paramètres de la première unité de la couche 1 et a³_1 se réfère à la valeur d'activation du premier neurone de la couche 1.

En résumé, une couche de neurones dans un réseau neuronal est un bloc de construction fondamental, et en comprenant comment construire une couche et comment utiliser ces blocs de construction, nous pouvons créer des réseaux neuronaux importants. De plus, l'utilisation de notations telles que les crochets carrés exponentiels peut nous aider à suivre les différentes couches dans un réseau neuronal.

Réseau complexe

nous allons explorer le concept des couches de réseaux neuronaux et comment elles fonctionnent pour construire des réseaux neuronaux plus complexes. Un réseau neuronal est un système d'algorithmes conçu pour reconnaître des motifs dans les données. Il est composé de couches de nœuds interconnectés, chacun exécutant une fonction spécifique.

Pour mieux comprendre ce concept, examinons un exemple d'un réseau neuronal plus complexe. Ce réseau a quatre couches, sans compter la couche d'entrée, également appelée couche 0. Les couches 1, 2 et 3 sont des couches cachées et la couche 4 est la couche de sortie. Par convention, lorsque nous disons qu'un réseau neuronal a quatre couches, cela inclut toutes les couches cachées et la couche de sortie, mais nous ne comptons pas la couche d'entrée.

Maintenant, concentrons-nous sur la couche 3, qui est la troisième et dernière couche cachée, pour regarder les calculs de cette couche. La couche 3 prend en entrée un vecteur, a_2, qui a été calculé par la couche précédente, et en sortie un vecteur a_3. Les calculs que la couche 3 effectue pour passer de a_2 à a_3 est en utilisant trois neurones ou nous appelons cela trois unités cachées, alors il a des paramètres w_1, b_1, w_2, b_2, et w_3, b_3 et il calcule a_1 égal à la fonction sigmoïde de w_1. produit avec cette entrée de la couche plus b_1, et il calcule a_2 égal à la fonction sigmoïde de w_2. produit avec à nouveau a_2, l'entrée de la couche plus b_2 et ainsi de suite pour obtenir a_3. Alors la sortie de cette couche est un vecteur comprenant a_1, a_2 et a_3.

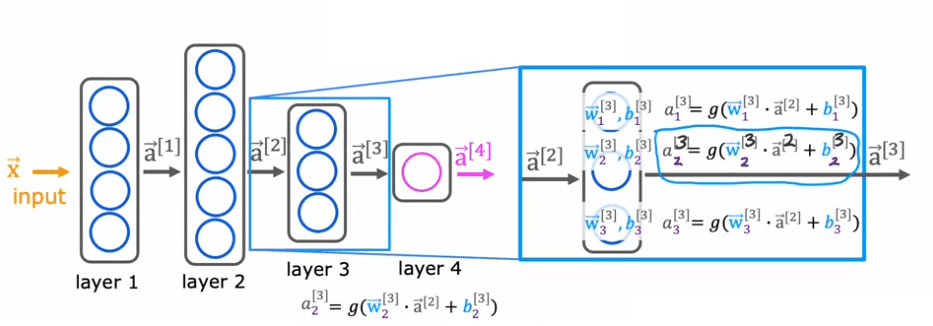
Pour utiliser la fonction d'activation, g, utilisons les paramètres de ce même neurone. Donc w et b auront le même indice 2 et crochets carrés exponentiels 3. Les caractéristiques d'entrée seront le vecteur de sortie de la couche précédente, qui est la couche 2. Ce sera donc le vecteur 'a' exposant 2.

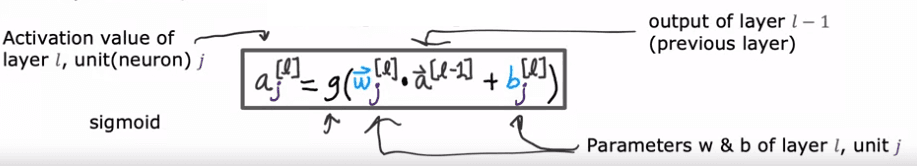
En résumé, un réseau neuronal est un système d'algorithmes conçu pour reconnaître des motifs dans les données. Il est composé de couches de nœuds interconnectés, chacun exécutant une fonction spécifique.

Dans cet section, nous avons utilisé un exemple de réseau neuronal plus complexe avec quatre couches et avons zoomé sur la couche 3 pour comprendre les calculs qui se produisent dans chaque couche. Nous avons également discuté de la façon dont la fonction d'activation et les paramètres sont utilisés pour passer d'une couche à l'autre. Comprendre le concept des couches de réseaux neuronaux et comment elles fonctionnent est crucial pour construire des réseaux neuronaux plus avancés.

Prédiction - Forward propagation

L'algorithme de propagation avant est utilisé pour faire des inférences ou des prévisions avec un réseau neuronal. Dans cet algorithme, les données d'entrée sont passées à travers les couches du réseau, effectuant des calculs à chaque couche, jusqu'à ce que la sortie finale soit produite.

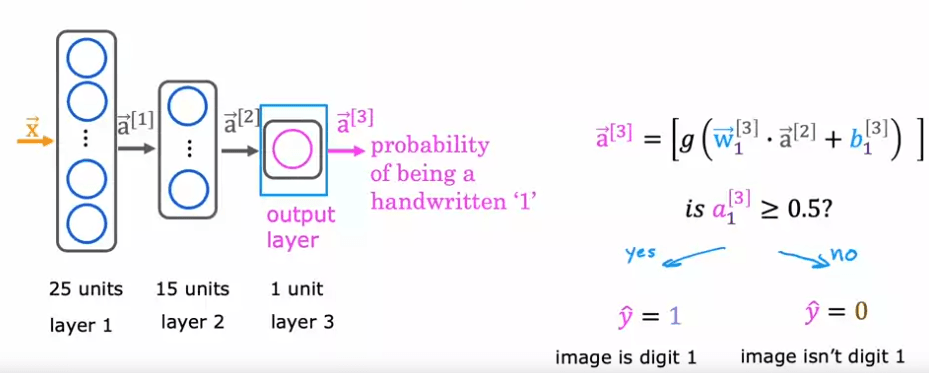
Par exemple, dans un problème de classification binaire de la distinction entre les chiffres manuscrits zéro et un, une image de huit par huit est entrée dans le réseau sous forme de 64 valeurs d'intensité de pixels. Le réseau neuronal utilisé dans cet exemple a deux couches cachées, avec la première couche cachée ayant 25 neurones et la seconde couche cachée ayant 15 neurones. La couche de sortie produit la probabilité prédite de l'image étant le chiffre un par rapport à zéro.

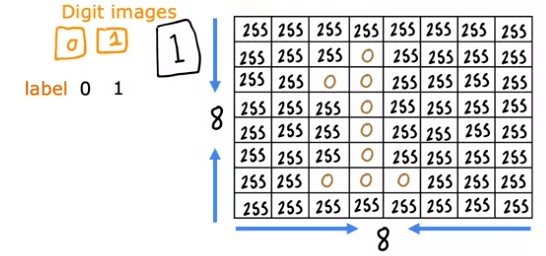
Nous pouvons définir :

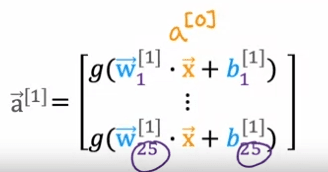
La première opération est de passer de l'entrée, X, à a1, qui est effectuée par la première couche de la première couche cachée en utilisant la formule à droite. La seconde étape consiste à calculer a2, qui est effectuée par la seconde couche cachée en utilisant une opération similaire. La dernière étape est de calculer a3, qui est effectuée par la couche de sortie en utilisant une opération similaire. La sortie, a3, est également la sortie du réseau neuronal et peut être écrite sous la forme f(x).

Implementation avec tensorflow

Le torréfaction des grains de café à la maison peut être une expérience amusante et enrichissante, surtout lorsque vous utilisez les bonnes techniques et outils pour obtenir la torréfaction parfaite. Un outil de ce type est l'utilisation d'un algorithme d'apprentissage pour optimiser la qualité des grains pendant le processus de torréfaction. La température et la durée de la torréfaction sont les entrées de l'algorithme et la sortie est la qualité des grains de café torréfiés.

En utilisant un jeu de données de différentes températures et durées, ainsi que des étiquettes indiquant la qualité des grains de café torréfiés, un algorithme d'apprentissage supervisé tel qu'un algorithme de régression peut être formé pour prédire la qualité de la torréfaction en fonction des entrées de température et de durée. Cela peut aider à garantir que les grains de café sont torréfiés à la perfection à chaque fois.

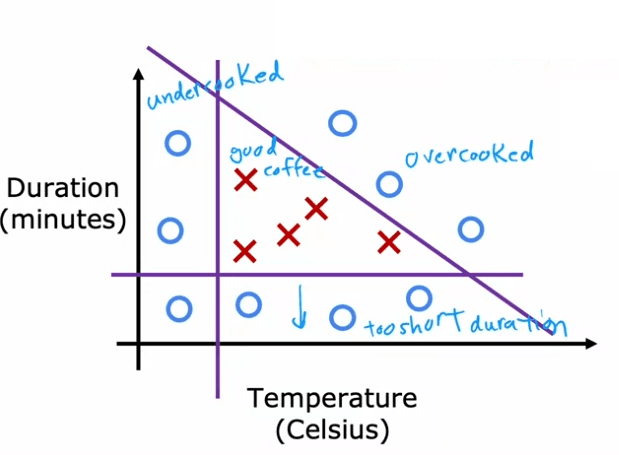
Dans un exemple simplifié, le jeu de données montre que si les grains sont cuits à une température trop basse, ils seront mal cuits. S'ils ne sont pas cuits assez longtemps, ils seront également mal cuits. Et s'ils sont cuits trop longtemps ou à une température trop élevée, ils seront brûlés. Seuls les points dans une plage de température et de durée spécifique donneront un bon café. En utilisant un algorithme d'apprentissage, nous pouvons déterminer cette plage idéale et ainsi garantir une torréfaction parfaite à chaque fois.

Cet exemple est simplifié, mais en réalité, il y a eu des projets importants utilisant l'apprentissage automatique pour optimiser la torréfaction du café. En utilisant un réseau neuronal, les entrées de température et de durée sont passées à travers les couches du réseau, effectuant des calculs à chaque couche, jusqu'à ce que la sortie finale soit produite, qui est la qualité prédite de la torréfaction.

Dans cet exemple, une couche dense avec 3 unités et une fonction d'activation sigmoïde est utilisée pour la première couche cachée et une couche dense avec 1 unité et une fonction d'activation sigmoïde est utilisée pour la deuxième couche cachée. La sortie finale, a2, est ensuite seuillée à 0,5 pour produire une classification binaire de café bon ou mauvais. Les détails supplémentaires tels que comment charger la bibliothèque TensorFlow et les paramètres du réseau neuronal peuvent être trouvés dans le laboratoire.

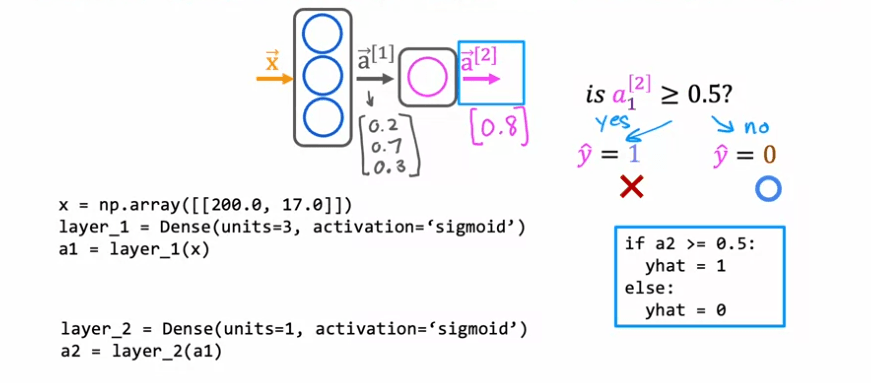
Ceci est un exemple de propagation avant, qui est la séquence de calculs effectués dans le réseau neuronal pour passer de l'entrée à la sortie finale. Il est appelé propagation avant car les activations des neurones sont propagées dans la direction avant de gauche à droite. Cela est en contraste avec un autre algorithme appelé propagation arrière ou backpropagation, qui est utilisé pour l'apprentissage. Il est important de noter que l'utilisation de l'apprentissage automatique pour optimiser la torréfaction du café est encore un domaine en développement et nécessite des recherches supplémentaires pour améliorer les résultats obtenus.

Explications avec Tensorflow

Dans cette section, nous discuterons de la façon de construire un réseau neuronal dans TensorFlow. À ce stade, vous devriez avoir une bonne compréhension de la façon de construire des couches et de réaliser une propagation avant dans TensorFlow. Nous allons prendre toutes ces connaissances et les mettre ensemble pour créer un réseau neuronal complet.

Une façon de construire un réseau neuronal dans TensorFlow consiste à initialiser les données manuellement, à créer la première couche, à calculer les activations, à créer la deuxième couche et à calculer à nouveau les activations. Cette méthode peut être chronophage et fastidieuse. Cependant, TensorFlow a une méthode plus simple de construire un réseau neuronal appelée la fonction séquentielle.

La fonction séquentielle nous permet de dire à TensorFlow de prendre deux couches et de les concaténer pour former un réseau neuronal. Cela élimine la nécessité de calculs manuels et permet à TensorFlow de faire beaucoup de travail pour nous. Par exemple, disons que nous avons un jeu d'entraînement comme celui-ci :

 X = np.array([[1,2], [3,4], [5,6], [7,8]])
Y = np.array([0, 1, 1, 0])

Prenons les données, X et Y, nous pouvons entrainer le modèle en réseau neuronal en appellant les deux fonctions suivantes :

 model.compile(...)
model.fit(X, Y)

Nous en apprendrons plus sur ces fonctions la semaine prochaine, mais pour l'instant, sachez qu'elles disent à TensorFlow de prendre le réseau neuronal que nous avons créé avec la fonction séquentielle et de l'entraîner sur les données X et Y.

Pour effectuer une inférence sur un nouvel exemple, nous appelons simplement la fonction model.predict() sur une nouvelle entrée, X_new. Cela produira la valeur correspondante de la couche finale, sans avoir besoin de calculs manuels.

En outre, TensorFlow a également une convention de ne pas attribuer explicitement les couches à des variables, mais plutôt d'utiliser le code suivant :

 model = Sequential()
model.add(Dense(3, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

Cette façon de coder est plus couramment vue dans le code TensorFlow, et c'est la même que l'exemple précédent, mais plus simple.

En résumé, construire un réseau neuronal dans TensorFlow est facilité par l'utilisation de la fonction séquentielle. Il permet un entraînement et une inférence plus rapides et efficaces, et la convention de ne pas attribuer explicitement les couches à des variables simplifie également le code. La semaine prochaine, nous plongerons plus en détail dans les paramètres spécifiques utilisés dans les fonctions model.compile() et model.fit(), ainsi que d'autres astuces et conseils pour coder en TensorFlow.

Numpy

Dans cette section, nous allons discuter de la mise en place de la propagation avant à partir de rien en Python. Cela est utile non seulement pour avoir une intuition sur ce qui se passe dans des bibliothèques comme TensorFlow et PyTorch, mais aussi pour ceux qui souhaitent construire quelque chose de mieux que ces frameworks à l'avenir.

Nous utiliserons un modèle de torréfaction de café en exemple pour démontrer le processus de propagation avant. La première étape est d'importer les bibliothèques nécessaires :

 import numpy as np

Les paramètres et les biais sont initialisés comme suit :

 w1_1, w1_2, w1_3 = 1.2, -3, 4
b1_1, b1_2, b1_3 = -1, 2, -0.5
w2_1 = -1
b2_1 = 0.5

Le vecteur de caractéristiques d'entrée est également initialisé :

 x = np.array([1, 2])

La première valeur à calculer est a1_1, qui est la première valeur d'activation de a1. Pour le calculer, nous avons les paramètres w1_1 et b1_1. Nous calculons z1_1 comme le produit scalaire entre le paramètre w1_1 et l'entrée x, et ajoutons b1_1. Enfin, a1_1 est égal à la fonction sigmoïde appliquée à z1_1 :

 z1_1 = np.dot(w1_1, x) + b1_1
a1_1 = 1 / (1 + np.exp(-z1_1))

Nous répétons le processus pour calculer a1_2 et a1_3 en utilisant les paramètres et les biais correspondants :

 z1_2 = np.dot(w1_2, x) + b1_2
a1_2 = 1 / (1 + np.exp(-z1_2))
z1_3 = np.dot(w1_3, x) + b1_3
a1_3 = 1 / (1 + np.exp(-z1_3))

Nous regroupons ensuite ces valeurs dans un tableau pour donner la sortie de la première couche, a1 :

 a1 = np.array([a1_1, a1_2, a1_3])

Nous mettons en place ensuite la seconde couche. La sortie a2 est calculée en utilisant le produit scalaire de a1 et le paramètre w2_1, en y ajoutant le terme de biais b2_1, et en appliquant la fonction sigmoïde :

 z2_1 = np.dot(w2_1, a1) + b2_1
a2_1 = 1 / (1 + np.exp(-z2_1))

Et c'est tout, c'est ainsi que vous pouvez implémenter la propagation avant à partir de rien en utilisant Python et numpy. Bien sûr, c'est un exemple très basique et pour un réseau neuronal plus général, le processus peut être simplifié à l'aide de boucles et de fonctions. Mais cet exemple fournit une base solide pour comprendre les concepts et les mécanismes sous-jacents de la propagation avant.

Nous allons explorer comment mettre en place la propagation avant à partir de zéro en Python. Cela nous aidera à mieux comprendre ce qui se passe derrière les coulisses des bibliothèques populaires telles que TensorFlow et PyTorch. Il est important de noter que ce n'est pas quelque chose que je recommande à la plupart des gens, car ces bibliothèques sont des outils puissants et efficaces. Cependant, comprendre comment mettre en place la propagation avant à partir de zéro peut être bénéfique pour toute personne souhaitant construire quelque chose de meilleur que TensorFlow et PyTorch.

Commençons par définir une fonction pour mettre en place une couche dense, qui est une seule couche d'un réseau de neurones. Nous appellerons cette fonction "dense". La fonction dense prend en entrée l'activation de la couche précédente, ainsi que les paramètres w et b pour les neurones d'une couche donnée.

Voici un exemple de la façon dont la fonction dense peut être utilisée pour mettre en place la propagation avant dans une seule couche :

 import numpy as np

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def dense(a, w, b):
    units = w.shape[1]
    a = np.zeros(units)
    for j in range(units):
        w_j = w[:, j]
        z = np.dot(w_j, a) + b[j]
        a[j] = sigmoid(z)
    return a

x = np.array([1, 2, 3])
w1 = np.array([[1, 2, -1], [-3, 4, 1], [2, -1, 3]])
b1 = np.array([-1, 1, 2])
a1 = dense(x, w1, b1)
print(a1)

Dans cet exemple, nous avons trois neurones dans la première couche et les paramètres w1, w2 et w3 sont empilés dans une matrice. De manière similaire, les paramètres b1, b2 et b3 sont empilés dans un tableau 1D. La fonction dense prend en entrée l'activation de la couche précédente, et les paramètres de la couche courante, et elle renvoie les activations pour la prochaine couche.

En utilisant la fonction dense, nous pouvons enchaîner ensemble quelques couches de manière séquentielle afin de mettre en œuvre la propagation avant dans un réseau de neurones. Par exemple, étant donné les caractéristiques d'entrée x, nous pouvons calculer les activations a1 comme a1 = dense(x, w1, b1) où w1 et b1 sont les paramètres de la première couche cachée. Ensuite, nous pouvons calculer a2 en tant que dense (a1, w2, b2) où w2 et b2 sont les paramètres de la seconde couche cachée. Nous pouvons continuer ce processus pour autant de couches que nous avons besoin dans le réseau de neurones.

Il est important de noter que ceci est un exemple simplifié et, en pratique, il existe de nombreuses techniques d'optimisation utilisées pour améliorer l'efficacité et la précision des réseaux de neurones. Cependant, en comprenant les bases de la façon dont la propagation avant peut être mise en œuvre à partir de zéro en Python, nous pouvons mieux comprendre les rouages des bibliothèques d'apprentissage profond populaires telles que TensorFlow et PyTorch.

Introduction

When neural networks were first invented, the goal was to create software that could mimic the way the human brain learns and thinks. While neural networks today are vastly different than the biological brain, the original motivations still play a role in how we think about them.

The human brain is considered the most advanced form of intelligence, and neural networks were created with the goal of building software that could mimic it. Work on neural networks began in the 1950s, but it fell out of favor for a while. In the 1980s and early 1990s, they gained popularity again and showed success in applications such as handwritten digit recognition. However, they fell out of favor again in the late 1990s.

It wasn't until about 2005 that neural networks enjoyed a resurgence and were rebranded as "deep learning." The term "deep learning" caught on because it sounds more impressive than "neural networks." Since then, neural networks have been used in a wide range of application areas including speech recognition, computer vision, natural language processing, and more.

Even though modern neural networks have little to do with how the brain actually works, the early motivation of trying to mimic the brain remains. To understand how the brain works, it's important to understand the structure of neurons. Neurons are the basic building blocks of the brain and are responsible for sending electrical impulses that make up human thought.

A simplified diagram of a biological neuron shows that it comprises a cell body, inputs (called dendrites), and outputs (called axons). The neuron receives electrical impulses from other neurons through its dendrites, processes them, and sends output impulses to other neurons through its axons. This process is repeated over and over, with the output of one neuron becoming the input of another, and so on.

When building an artificial neural network or deep learning algorithm, the basic building block is the neuron. A neuron takes one or more inputs, which are simply numbers, performs some computation, and outputs another number. These outputs can then be used as inputs for other neurons. In this way, many neurons can be simulated at the same time to create a network.

In this diagram, three neurons are shown working together. They input a few numbers, perform computation, and output other numbers. However, it's important to note that while there is a loose analogy between biological neurons and artificial neurons, we currently have a limited understanding of how the human brain actually works.

In summary, neural networks were created with the goal of mimicking the way the human brain learns and thinks. While the technology has come a long way since its inception, the original motivations remain an important part of how we think about neural networks today.

Demand Prediction

When building a neural network, it's important to understand the basic building block: the neuron. A neuron takes one or more inputs, which are simply numbers, performs some computation, and outputs another number. These outputs can then be used as inputs for other neurons. In this way, many neurons can be simulated at the same time to create a network.

To illustrate this concept, let's take an example of demand prediction for T-shirts.

• The goal is to predict if a T-shirt will be a top seller or not, based on data such as the price of the T-shirt and whether or not it became a top seller in the past.
• This type of application is used by retailers to plan better inventory levels and marketing campaigns.

In this example, the input feature x is the price of the T-shirt, and the goal is to predict if a particular T-shirt will be a top seller or not. To do this, we use logistic regression to fit a sigmoid function to the data. The output of the prediction is represented by the formula: f(x) = 1/1 + e^(-wx + b) where w and b are parameters learned during the training of the model.

This output, which we denote as a, represents the probability of the T-shirt being a top seller. Another way to think of it is that this logistic regression unit can be thought of as a simplified model of a single neuron in the brain. It takes in the input feature, price, and computes the output, probability of the T-shirt being a top seller.

To create a neural network, we take a number of these logistic regression units and wire them together to make a final prediction. In this example, we have 4 features to predict whether or not a T-shirt is a top seller. The features are:

• The price of the T-shirt
• The shipping costs
• The amounts of marketing of that particular T-shirt
• The material quality, is this a high-quality, thick cotton versus maybe a lower quality material?

Each of these features is input into a separate logistic regression unit, which compute the probability of T-shirt being affordable, having high awareness, or being perceived as high quality. These probabilities are then combined to make a final prediction of whether or not the T-shirt will be a top seller.

Each features is called, input layer as vector X (X->). They are inserted into hidden layer, called vector (A->) or activations, to go to the final output layer which provide the probability A.

It's important to note that while the logistic regression algorithm is a simplified model of a single neuron in the brain, deep learning algorithms do work very well in practice. Building a neural network involves taking a number of these neurons and wiring them together to make a prediction.

Neuronal network model

The building blocks of most neural networks are layers of neurons. In this article, we will explore how to construct a layer of neurons and how to use these building blocks to create a larger neural network.

As an example, let's consider a demand prediction problem where we have four input features fed into a hidden layer with three neurons. These three neurons then send their output to an output layer with one neuron.

To understand how the hidden layer functions, let's take a closer look at the computations. The hidden layer inputs four numbers, which are then passed to each of the three neurons. Each neuron is essentially a logistic regression unit, with its own parameters (w and b). For example, the first neuron has parameters w_1 and b_1, and it outputs an activation value a, which is calculated as g(w_1 * x + b_1), where g is the logistic function and x is the input. This activation value, a_1, represents the probability of the input being highly affordable.

Similarly, the second neuron has parameters w_2 and b_2 and calculates an activation value a_2, which represents the probability of potential buyers being aware of the product. The third neuron has parameters w_3 and b_3 and calculates an activation value a_3. The vector of these three activation values, [a_1, a_2, a_3], is then passed to the final output layer of the neural network.

When building neural networks with multiple layers, it is useful to give the layers different numbers. By convention, the input layer is called layer 0, this hidden layer is called layer 1, and the output layer is called layer 2. However, today neural networks can have dozens or even hundreds of layers. To keep track of the different layers, we can use superscript square brackets to indicate which layer we are referring to. For example, a⁴ refers to the output of layer 1, w⁵_1 refers to the parameters of the first unit in layer 1, and a⁶_1 refers to the activation value of the first neuron in layer 1.

In summary, a layer of neurons in a neural network is a fundamental building block, and by understanding how to construct a layer and how to use these building blocks, we can create large neural networks. Additionally, using notation such as superscript square brackets can help us keep track of different layers in a neural network.

More complex network

We will be exploring the concept of neural network layers and how they work to build more complex neural networks. A neural network is a system of algorithms that is designed to recognize patterns in data. It is made up of layers of interconnected nodes, each of which performs a specific function.

To better understand this concept, let's take a look at an example of a more complex neural network. This network has four layers, not counting the input layer, which is also called Layer 0. Layers 1, 2, and 3 are hidden layers, and Layer 4 is the output layer. By convention, when we say that a neural network has four layers, that includes all the hidden layers in the output layer, but we don't count the input layer.

Now, let's zoom in to Layer 3, which is the third and final hidden layer to look at the computations of that layer. Layer 3 inputs a vector, a_2, that was computed by the previous layer, and it outputs a_3, which is another vector. The computation that Layer 3 does to go from a_2 to a_3 is using three neurons or we call it three hidden units, then it has parameters w_1, b_1, w_2, b_2, and w_3, b_3 and it computes a_1 equals sigmoid of w_1. product with this input to the layer plus b_1, and it computes a_2 equals sigmoid of w_2. product with again a_2, the input to the layer plus b_2 and so on to get a_3. Then the output of this layer is a vector comprising a_1, a_2, and a_3.

To apply the activation function, g, lets use the parameters of this same neuron. So w and b will have the same subscript 2 and superscript square bracket 3. The input features will be the output vector from the previous layer, which is layer 2. So that will be the vector 'a' superscript 2.

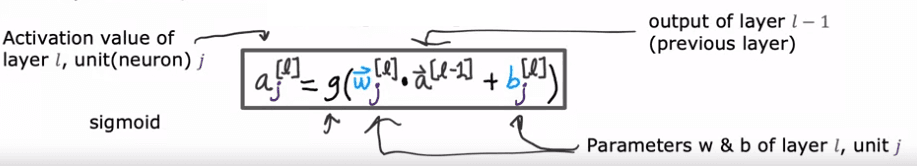
In summary, a neural network is a system of algorithms that is designed to recognize patterns in data. It is made up of layers of interconnected nodes, each of which performs a specific function. In this article, we used a more complex neural network example with four layers and zoomed in to Layer 3 to understand the computations that happen in each layer. We also discussed how the activation function and parameters are used to go from one layer to another. Understanding the concept of neural network layers and how they work is crucial in building more advanced neural networks.

Prediction - Forward propagation

The forward propagation algorithm is used to make inferences or predictions with a neural network. In this algorithm, input data is passed through the layers of the network, making computations at each layer, until the final output is produced.

For example, in a binary classification problem of distinguishing between the handwritten digits zero and one, an eight by eight image is inputted into the network as 64 pixel intensity values. The neural network used in this example has two hidden layers, with the first hidden layer having 25 neurons and the second hidden layer having 15 neurons. The output layer produces the predicted probability of the image being the digit one versus zero.

The first computation is to go from the input, X, to a1, which is done by the first layer of the first hidden layer using the formula on the right. The second step is to compute a2, which is done by the second hidden layer using a similar computation. The final step is to compute a3, which is done by the output layer using a similar computation. The output, a3, is also the output of the neural network and can be written as f(x).

We can define :

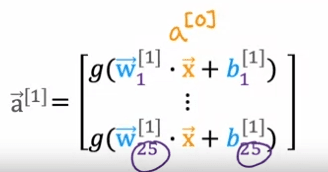
The sequence of computations made in the forward propagation algorithm is called forward propagation because the activations of the neurons are being propagated in the forward direction from left to right. This is in contrast to a different algorithm called backward propagation or backpropagation, which is used for learning. This type of neural network architecture, where the number of hidden units decreases as you get closer to the output layer, is a typical choice when choosing neural network architectures. With this understanding of forward propagation, you can now make inferences with your neural network.

Implementation with tensorflow

Roasting coffee beans at home can be a fun and rewarding experience, especially when using the right techniques and tools to achieve the perfect roast. One such tool is using a learning algorithm to optimize the quality of the beans during the roasting process. The temperature and duration of the roast are the inputs to the algorithm, and the output is the quality of the roasted coffee beans.

Using a dataset of different temperatures and durations, as well as labels indicating the quality of the roasted coffee beans, a supervised learning algorithm such as a regression algorithm can be trained to predict the quality of the roast based on the temperature and duration inputs. This can help ensure that the coffee beans are roasted to perfection every time.

In a simplified example, the dataset shows that if the beans are cooked at too low of a temperature, they will be undercooked. If they are not cooked for long enough, they will also be undercooked. And if they are cooked for too long or at too high of a temperature, they will be burnt. Only points within a specific temperature and duration range will result in good coffee.

This example is simplified, but in actuality, there have been serious projects using machine learning to optimize coffee roasting. Using a neural network, the temperature and duration inputs are passed through layers of the network, making computations at each layer, until the final output is produced, which is the predicted quality of the roast.

In this example, a dense layer with 3 units and a sigmoid activation function is used for the first hidden layer and a dense layer with 1 unit and a sigmoid activation function is used for the second hidden layer. The final output, a2, is then thresholded at 0.5 to produce a binary classification of good or bad coffee. The additional details such as how to load the TensorFlow library and the parameters of the neural network can be found in the lab.

This is an example of forward propagation, which is the sequence of computations made in the neural network to go from the input to the final output. It's called forward propagation because the activations of the neurons are being propagated in the forward direction from left to right. This is in contrast to a different algorithm called backward propagation or backpropagation, which is used for learning.

Tensorflow explications

In this sections, we will be discussing how to build a neural network in TensorFlow. By now, you should have a good understanding of how to build layers and perform forward propagation in TensorFlow. We will be taking all of that knowledge and putting it together to create a complete neural network.

One way to build a neural network in TensorFlow is to manually initialize the data, create layer one, compute the activations, create layer two, and compute the activations again. This method can be time-consuming and tedious. However, TensorFlow has a simpler way of building a neural network called the sequential function.

The sequential function allows us to tell TensorFlow to take two layers and string them together to form a neural network. This eliminates the need for manual computation and allows TensorFlow to do a lot of the work for us. For example, let's say we have a training set like this:

 X = np.array([[1,2], [3,4], [5,6], [7,8]])
Y = np.array([0, 1, 1, 0])

Given the data, X and Y, we can train the neural network by calling the following two functions:

 model.compile(...)
model.fit(X, Y)

We will learn more about these functions next week, but for now, just know that they tell TensorFlow to take the neural network we created with the sequential function and train it on the data, X and Y.

In order to perform inference on a new example, we simply call the model.predict() function on a new input, X_new. This will output the corresponding value of the final layer, without the need for manual computation.

In addition to this, TensorFlow also has a convention of not explicitly assigning the layers to variables, but instead using the following code:

 model = Sequential()
model.add(Dense(3, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

This way of coding is more commonly seen in TensorFlow code, and it's the same as the previous example, but simpler.

In summary, building a neural network in TensorFlow is made easy with the use of the sequential function. It allows for faster and more efficient training and inference, and the convention of not explicitly assigning layers to variables also simplifies the code. Next week, we will delve deeper into the specific parameters used in the model.compile() and model.fit() functions, as well as other tips and tricks for coding in TensorFlow.

Numpy

we will be discussing how to implement forward propagation from scratch in Python. This is not only useful for gaining intuition about what's happening in libraries like TensorFlow and PyTorch, but also for those who may want to build something even better than these frameworks in the future.

We will be using a coffee roasting model as an example to demonstrate the process of forward propagation. The first step is to import the necessary libraries:

 import numpy as np

The parameters and biases are initialized as follows:

 w1_1, w1_2, w1_3 = 1.2, -3, 4
b1_1, b1_2, b1_3 = -1, 2, -0.5
w2_1 = -1
b2_1 = 0.5

The input feature vector is also initialized:

 x = np.array([1, 2])

The first value to compute is a1_1, which is the first activation value of a1. To compute this, we have parameters w1_1 and b1_1. We compute z1_1 as the dot product between the parameter w1_1 and the input x, and add b1_1. Finally, a1_1 is equal to the sigmoid function applied to z1_1:

 z1_1 = np.dot(w1_1, x) + b1_1
a1_1 = 1 / (1 + np.exp(-z1_1))

We repeat the process to compute a1_2 and a1_3 using the corresponding parameters and biases:

 z1_2 = np.dot(w1_2, x) + b1_2
a1_2 = 1 / (1 + np.exp(-z1_2))
z1_3 = np.dot(w1_3, x) + b1_3
a1_3 = 1 / (1 + np.exp(-z1_3))

We then group these values together into an array to give the output of the first layer, a1:

 a1 = np.array([a1_1, a1_2, a1_3])

We then implement the second layer. The output a2 is computed using the dot product of a1 and the parameter w2_1, added to the bias term b2_1, and applying the sigmoid function:

 z2_1 = np.dot(w2_1, a1) + b2_1
a2_1 = 1 / (1 + np.exp(-z2_1))

And that's it, that's how you can implement forward propagation from scratch in Python using numpy. Of course, this is a very basic example and for a more general neural network, the process can be simplified using loops and functions. But this example provides a solid foundation for understanding the underlying concepts and mechanics of forward propagation.

we will explore how to implement forward propagation from scratch in Python. This will help us gain a better understanding of what's happening behind the scenes in popular libraries like TensorFlow and PyTorch. It's important to note that this is not something that I would recommend for most people, as these libraries are powerful and efficient tools. However, understanding how to implement forward prop from scratch can be beneficial for anyone who wants to build something even better than TensorFlow and PyTorch.

Let's start by defining a function to implement a dense layer, which is a single layer of a neural network. We will call this function "dense". The dense function takes as input the activation from the previous layer, as well as the parameters w and b for the neurons in a given layer.

Here is an example of how the dense function can be used to implement forward prop in a single layer:

 import numpy as np

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def dense(a, w, b):
    units = w.shape[1]
    a = np.zeros(units)
    for j in range(units):
        w_j = w[:, j]
        z = np.dot(w_j, a) + b[j]
        a[j] = sigmoid(z)
    return a

x = np.array([1, 2, 3])
w1 = np.array([[1, 2, -1], [-3, 4, 1], [2, -1, 3]])
b1 = np.array([-1, 1, 2])
a1 = dense(x, w1, b1)
print(a1)

In this example, we have three neurons in the first layer and the parameters w1, w2, and w3 are stacked into a matrix. Similarly, the parameters b1, b2, and b3 are stacked into a 1D array. The dense function takes as input the activation from the previous layer, and the parameters for the current layer, and it returns the activations for the next layer.

Given the dense function, we can string together a few dense layers sequentially in order to implement forward prop in a neural network. For example, given the input features x, we can compute the activations a1 as a1 = dense(x, w1, b1) where w1 and b1 are the parameters of the first hidden layer. Then we can compute a2 as dense(a1, w2, b2) where w2 and b2 are the parameters of the second hidden layer. We can continue this process for as many layers as we need in the neural network.

It's important to note that this is a simplified example and in practice, there are many optimization techniques that are used to improve the efficiency and accuracy of neural networks. However, by understanding the basics of how forward prop can be implemented from scratch in Python, we can better understand the inner workings of popular deep learning libraries like TensorFlow and PyTorch.

L'entrainement avec tensorflow

La construction d'un modèle de régression logistique implique plusieurs étapes, notamment la spécification de la façon de calculer la sortie en fonction de la variable d'entrée x et des paramètres w et b. La première étape consiste à définir la fonction de régression logistique, qui prédit f(x) comme la fonction sigmoïde appliquée au produit scalaire de w et x plus b:

La deuxième étape consiste à spécifier la fonction de perte, qui mesure la performance du modèle de régression logistique sur un exemple d'entraînement unique (x, y). La fonction coût, qui est la moyenne de la fonction de perte calculée sur l'ensemble de l'ensemble d'entraînement, est également définie à cette étape.

La dernière étape consiste à utiliser un algorithme, tel que la descente de gradient, pour minimiser la fonction coût J(w, b) en fonction des paramètres w et b. Cela se fait en mettant à jour w et b en utilisant la dérivée de J par rapport à w et b, respectivement. Ces trois étapes - spécifier la fonction de sortie, spécifier les fonctions de perte et de coût et minimiser la fonction coût - sont les étapes clés dans la construction et la formation d'un modèle de régression logistique.

Les mêmes trois étapes peuvent également être appliquées à l'entraînement d'un réseau neuronal dans TensorFlow. Pour spécifier la fonction de sortie, l'architecture du réseau neuronal est définie, y compris le nombre d'unités cachées et la fonction d'activation utilisée:

 model = Sequential(
    [
        tf.keras.Input(shape=(400,)),    #specify input size
        ### START CODE HERE ###
        Dense(25, activation='sigmoid', name = 'layer1'),
        Dense(15, activation='sigmoid', name = 'layer2'),
        Dense(1, activation='sigmoid', name = 'layer3')
        ### END CODE HERE ###
    ], name = "my_model"
)

La fonction de perte, telle que la fonction de perte d'entropie croisée binaire, est spécifiée à la deuxième étape:

 model.compile(

    loss=tf.keras.losses.BinaryCrossentropy(),

    optimizer=tf.keras.optimizers.Adam(0.001),

)

Et la dernière étape consiste à minimiser la fonction coût en utilisant une fonction telle que la descente de gradient.

 model.fit(
    X,y,
    epochs=20
)

Globalement, le processus de formation d'un modèle de régression logistique et d'un réseau neuronal dans TensorFlow sont similaires et peuvent être compris en les décomposant en ces trois étapes.