Introduction

Le machine learning, inventé dans les années 1960, est une combinaison de deux mots : "machine" qui fait référence à un ordinateur, un robot ou tout autre appareil, tandis que "learning" désigne l'activité de découvrir des motifs dans des événements où les humains excellent. Il permet aux machines d'acquérir des connaissances humaines sans les limitations des contraintes humaines telles que les grèves, la fatigue ou la maladie. Cependant, il est important de noter que le machine learning n'est pas simplement de l'automatisation. Contrairement à un mythe populaire, le machine learning n'est pas identique à l'automatisation car il implique des tâches instructives et répétitives sans réflexion au-delà. S'il était possible d'embaucher de nombreux programmeurs de logiciels et de continuer à programmer de nouvelles règles ou à étendre les anciennes, la solution deviendrait coûteuse avec le temps en raison des nombreuses variations qui pourraient apparaître.

Programmation traditionelle	Apprentissage automatique
L'ordinateur applique un ensemble prédéfini de règles pour traiter les données d'entrée et générer un résultat en conséquence.	L'ordinateur tente d'émuler le processus de pensée humaine en interagissant avec les données d'entrée, l'environnement et les résultats attendus, à partir desquels il déduit des modèles représentés par un ou plusieurs modèles mathématiques. Ces modèles sont ensuite utilisés pour interagir avec les données d'entrée futures et produire des résultats sans instruction explicite et directive.

Le domaine du machine learning est étroitement lié à des disciplines telles que l'algèbre linéaire, la théorie des probabilités, les statistiques et l'optimisation mathématique. Nous construisons souvent des modèles d'apprentissage automatique en utilisant des concepts statistiques, de probabilités et d'algèbre linéaire, puis optimisons ces modèles à travers des techniques d'optimisation mathématique.

Les types d'apprentissage

La fonction principale de l'apprentissage automatique consiste à explorer et à développer des algorithmes qui peuvent apprendre à partir de données historiques et faire des prédictions sur de nouvelles données d'entrée. Pour une solution axée sur les données, il est nécessaire de définir une fonction d'évaluation appelée fonction de perte ou de coût, qui mesure l'efficacité des modèles d'apprentissage.

Il existe trois catégories d'apprentissage :

• L'apprentissage non supervisé: dans lequel les données ne disposent pas de description préalable, nécessitant ainsi l'identification de la structure des données. Les données non étiquetées peuvent être utilisées pour détecter des anomalies, telles que des fraudes ou des équipements défectueux, ou pour regrouper des clients ayant des comportements en ligne similaires pour une campagne marketing.

• L'apprentissage supervisé: dans lequel les données sont fournies avec des descriptions, des objectifs et des résultats souhaités. Les données étiquetées sont ensuite utilisées pour apprendre une règle qui peut être utilisée pour étiqueter les nouvelles données avec une sortie inconnue. Les étiquettes sont généralement fournies par des systèmes d'enregistrement d'événements ou évaluées par des experts humains. L'apprentissage supervisé est utilisé pour la reconnaissance faciale et vocale, les recommandations de produits ou de films, les prévisions de ventes et la détection de courrier indésirable.

• L'apprentissage par renforcement: qui est utilisé pour des applications telles que la robotique industrielle, les voitures autonomes et les jeux tels que le maître d'échecs AlphaGo. La principale différence entre l'apprentissage par renforcement et l'apprentissage supervisé réside dans l'interaction avec l'environnement.

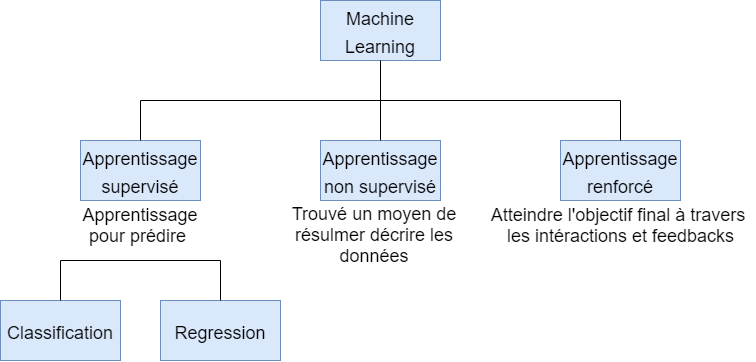
L'apprentissage non supervisé peut prendre deux formes distinctes:

• La régression non supervisée : qui permet de prédire des valeurs continues telles que les prix des logements, par exemple.

-La classification non supervisée : qui permet de trouver l'étiquette de classe appropriée, par exemple en analysant un sentiment positif/négatif et en prédisant un défaut de paiement.

Dans certains cas, certains échantillons d'apprentissage peuvent être étiquetés tandis que d'autres ne le sont pas. Cela conduit à ce qu'on appelle l'apprentissage semi-supervisé.

Les données

Le monde actuel produit une énorme quantité de données, comprenant à la fois des données de qualité et des données erronées. L'un des principaux défis dans le traitement de ces données est leur diversité et leur imprécision. Les ordinateurs fonctionnent en utilisant des signaux électriques qui sont ensuite traduits en codes binaires 0 et 1. Dans le domaine de la programmation en langage Python, par exemple, les données sont normalement représentées sous forme de nombres, d'images ou de textes. Cependant, pour les algorithmes de machine learning, il est souvent nécessaire de convertir les images et le texte en données numériques afin de les traiter efficacement.

Dans le domaine de l'apprentissage machine, les données sont souvent divisées en trois ensembles :

• les ensembles d'apprentissage
• les ensembles de validation
• les ensembles de test.

Les ensembles d'apprentissage sont utilisés pour entraîner les modèles d'apprentissage, tandis que les ensembles de validation sont utilisés pour évaluer la performance de ces modèles pendant le processus d'apprentissage. Les ensembles de test sont finalement utilisés pour mesurer la performance des modèles d'apprentissage sur des données inconnues, et ainsi déterminer leur efficacité réelle. Pour généraliser les modèles d'apprentissage et les rendre applicables à des données inconnues, il est donc crucial d'utiliser des ensembles de données variées et de qualité, tout en prenant en compte les imprécisions et les différences qui peuvent exister entre les différents types de données.

Surapprentissage, sous-apprentissage et compromis biais-variance

Surapprentissage

Le surapprentissage, également connu sous le nom de surajustement, se produit lorsque le modèle d'apprentissage est trop complexe et est entraîné sur un ensemble de données trop restreint, ce qui entraîne une correspondance excessive avec les observations existantes. Bien que le modèle puisse fonctionner parfaitement avec les données d'entraînement, il peut ne pas être capable de généraliser et de prédire de nouvelles observations à l'extérieur de cet ensemble de données.

Le surapprentissage est souvent causé par une surutilisation des données d'entraînement, ce qui peut conduire à la mémorisation plutôt qu'à la compréhension du modèle. Cela peut être évité en utilisant des techniques telles que la validation croisée et le réglage des hyperparamètres, qui permettent de sélectionner le modèle le plus approprié et d'éviter les biais.

Le biais, quant à lui, est une mesure de l'exactitude moyenne des prévisions d'un modèle par rapport aux valeurs réelles. Un modèle avec un biais élevé peut être biaisé en raison d'hypothèses erronées ou de l'utilisation d'un modèle trop simple pour capturer la complexité des données. Dans le domaine de l'apprentissage machine, il est important de trouver le bon équilibre entre le biais et la variance, afin de maximiser la performance prédictive du modèle.

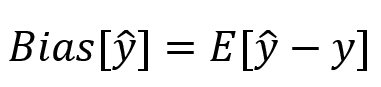
note: ^y => la prédiction

Une variance élevée dans un modèle d'apprentissage signifie qu'il fonctionne mal sur des ensembles de données qui n'ont pas été vus auparavant. La variance mesure la capacité du modèle à s'adapter à de nouvelles hypothèses, et donc la variabilité des prédictions. Un modèle avec une variance élevée peut être trop complexe et peut surapprendre les données d'entraînement, conduisant à une faible performance sur les données de test.

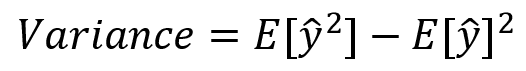
Nous pouvons représenté le surapprentissage :

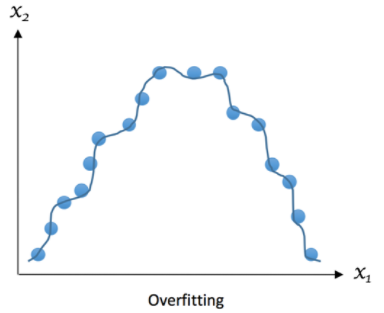
Le surapprentissage est souvent causé par une surutilisation des données d'entraînement et une complexité excessive du modèle. En essayant de décrire les règles d'apprentissage en se basant sur trop de paramètres par rapport au petit nombre d'observations, le modèle peut surapprendre les données d'entraînement au lieu de capturer la relation sous-jacente. Par exemple, si nous disposons de seulement quelques exemples d'apprentissage pour distinguer entre les pommes de terre et les tomates, et que nous essayons de déduire de nombreuses caractéristiques pour les distinguer, notre modèle risque de surapprendre les exemples d'apprentissage spécifiques plutôt que de saisir les traits distinctifs des pommes de terre et des tomates.

Le surapprentissage peut également être causé par un modèle trop complexe, qui peut s'adapter de manière excessive aux données d'entraînement, ce qui peut conduire à une mauvaise performance sur les données de test. Par exemple, si nous créons un modèle qui mémorise toutes les réponses à toutes les questions de l'ensemble d'apprentissage, il peut être très précis sur l'ensemble d'apprentissage, mais sera incapable de généraliser à de nouveaux exemples de questions.

Sous-apprentissage

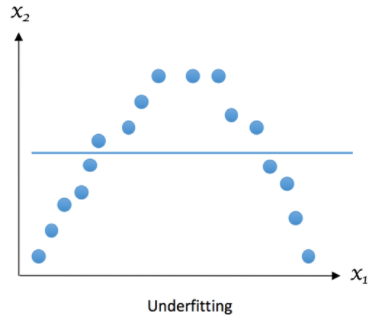
Le sous-apprentissage est un phénomène qui se produit lorsque le modèle n'est pas capable de capturer la tendance ou la structure sous-jacente des données. Cela peut se produire si le modèle est trop simple et ne contient pas suffisamment de paramètres pour capturer la complexité des données, ou si le modèle est mal choisi pour le type de données en question.

Un sous-apprentissage peut également se produire si nous n'avons pas suffisamment de données pour entraîner le modèle de manière adéquate. Dans ce cas, le modèle peut être trop généralisé et ne pas être capable de saisir les variations subtiles dans les données.

Le résultat que nous espérons peut être représenté comme ceci :

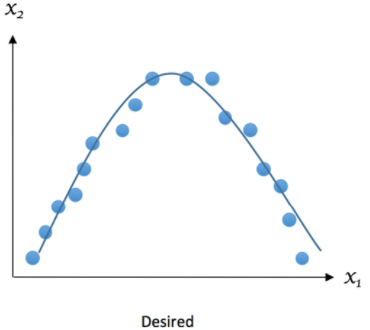
Un biais élevé est souvent associé au sous-apprentissage, car le modèle est incapable de capturer la structure sous-jacente des données. Cela peut entraîner une performance cohérente mais insuffisante sur les ensembles d'entraînement et de test, ce qui indique une faible variance. Pour résoudre le sous-apprentissage, il est souvent nécessaire d'utiliser des modèles plus complexes ou d'ajouter des fonctionnalités supplémentaires pour capturer les détails manquants dans les données. De plus, l'augmentation de la taille de l'ensemble de données peut également aider à améliorer la performance du modèle et à éviter le sous-apprentissage.

Le compromis biais-variance

Nous devons éviter les cas où le biais ou la variance deviennent élevés. Cela signifie-t-il que nous devrions toujours réduire au maximum le biais et la variance ? La réponse est oui, si c'est possible. Toutefois, dans la pratique, il y a un compromis explicite entre les deux, où la diminution de l'un augmente l'autre : c'est le compromis biais-variance.

Nous voulons créer un modèle capable de prédire l'élection d'un président. Pour cela, nous réalisons des sondages téléphoniques par code postal pour obtenir des échantillons. Nous prélevons des échantillons au hasard dans un code postal et estimons que le président X sera élu avec une probabilité de 61 %. Cependant, le président X n'est pas élu, alors pourquoi ? La première chose à laquelle nous pensons est la petite taille des échantillons d'un seul code postal, qui est également une source de biais élevé. Les personnes d'une zone géographique ont tendance à partager des données démographiques similaires, ce qui entraîne une faible variance des estimations. Est-ce que l'utilisation d'échantillons de plusieurs codes postaux peut corriger cela ? Oui, mais cela pourrait entraîner simultanément une augmentation de la variance des estimations : c'est le compromis biais-variance.

Nous pouvons mesurer l'erreur quadratique moyenne (MSE) : étant donné un ensemble d'échantillons d'apprentissage x1, x2, …, xn et leurs cibles y1, y2, …, yn, nous voulons trouver une fonction de régression (x) qui estime correctement la vraie relation y (x).

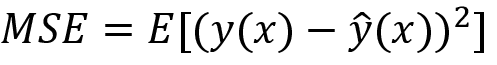
Ici E désigne l'attente. Cette erreur peut être décomposée en composants de biais et de variance à la suite de la dérivation analytique.

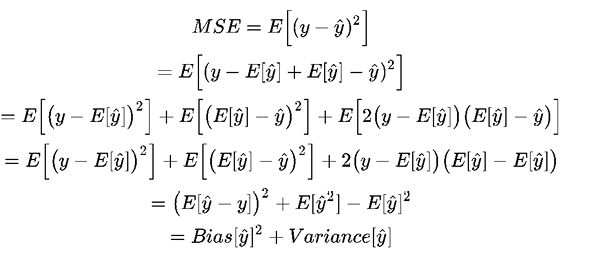
Le biais mesure l'erreur systématique des estimations, tandis que la variance décrit la quantité avec laquelle l'estimation ŷ se déplace autour de sa moyenne, E[y]. Plus le modèle d'apprentissage ŷ(x) est complexe et plus la taille des échantillons d'apprentissage est grande, plus le biais tend à diminuer. Cependant, cela peut également entraîner une augmentation de la variance du modèle pour mieux s'adapter aux points de données supplémentaires.

La validation croisée

La procédure de validation est une étape cruciale pour évaluer comment les modèles se généralisent à des ensembles de données indépendants dans un domaine donné. Dans un cadre de validation conventionnel, les données d'origine sont généralement partitionnées en trois sous-ensembles: 60 % pour l'apprentissage, 20% pour la validation et 20% pour les tests. Bien que cela soit suffisant si nous avons suffisamment d'échantillons d'apprentissage, dans le cas contraire, la validation croisée est préférable.

Dans un cycle de validation croisée, les données d'origine sont divisées en deux sous-ensembles: l'apprentissage et les tests (ou validation). La validation croisée est un moyen efficace de réduire la variabilité et donc de limiter le surapprentissage. Il y a principalement deux schémas de validation croisée utilisés : le schéma exhaustif et le schéma "k-fold".

Le schéma exhaustif consiste à émettre un nombre fixe d'observations à chaque tour comme échantillons des tests (validation), pour utiliser les observations restantes comme échantillons d'apprentissage. On répète alors ce processus jusqu'à ce que tous les différents sous-ensembles d'échantillons soient utilisés pour le test au moins une fois. Leave-One-Out-Cross-Validation (LOOCV) est un exemple de ce schéma : pour un ensemble de données de taille n, LOOCV nécessite n cycles de validation croisée. Cependant, cela peut être lent lorsque n devient grand.

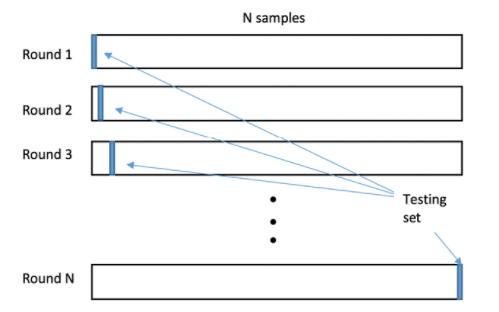
Le schéma "k-fold" consiste à diviser les données en k sous-ensembles égaux. Chaque sous-ensemble est utilisé tour à tour comme ensemble de tests, tandis que les autres sous-ensembles sont utilisés comme ensemble d'apprentissage. Ce processus est répété k fois, en utilisant chaque sous-ensemble une fois comme ensemble de tests. La validation croisée "k-fold" est généralement plus rapide que le schéma exhaustif, tout en produisant des estimations de performance plus stables.

Tour
1	Test	Entraînement	Entraînement	Entraînement	Entraînement
2	Entraînement	Test	Entraînement	Entraînement	Entraînement
3	Entraînement	Entraînement	Test	Entraînement	Entraînement
4	Entraînement	Entraînement	Entraînement	Test	Entraînement
5	Entraînement	Entraînement	Entraînement	Entraînement	Test

La validation croisée "k-fold" est généralement préférable à Leave-One-Out-Cross-Validation (LOOCV) en raison de sa variance plus faible. Cela est dû au fait que la validation croisée "k-fold" utilise un bloc d'échantillons pour la validation au lieu d'un seul, comme c'est le cas avec LOOCV.

Cependant, la validation croisée imbriquée est une combinaison de validations croisées qui comporte deux phases distinctes. La première phase, appelée validation croisée interne, est utilisée pour trouver le meilleur ajustement du modèle. Elle peut être implémentée sous la forme d'une validation croisée "k-fold". Dans cette phase, le modèle est ajusté sur des sous-ensembles d'apprentissage et évalué sur des sous-ensembles de validation.

La seconde phase, appelée validation croisée externe, est utilisée pour l'évaluation des performances et l'analyse statistique du modèle ajusté dans la phase précédente. Cette phase utilise également une validation croisée "k-fold", où le modèle est ajusté sur des sous-ensembles d'apprentissage et évalué sur des sous-ensembles de tests différents de ceux utilisés dans la phase interne.

En utilisant la validation croisée imbriquée, nous pouvons évaluer la capacité de généralisation d'un modèle de manière plus précise et plus robuste. Cela est particulièrement important lorsque la taille de l'ensemble de données est petite ou lorsque nous utilisons des modèles complexes qui peuvent surapprendre les données.

Régularisation

La régularisation est une technique qui consiste à ajouter des paramètres à la fonction d'erreur dans le but de limiter la complexité des modèles. Les modèles polynomiaux sont plus nombreux que les modèles linéaires car ces derniers sont déterminés par deux paramètres seulement : l'interception et la pente. La dimension de l'espace de recherche des coefficients pour une ligne est donc deux. En revanche, un polynôme quadratique ajoute un coefficient supplémentaire pour le terme quadratique, ce qui étend l'espace de recherche à trois dimensions. De ce fait, il est plus facile de trouver un modèle polynômial d'ordre élevé qui correspond parfaitement à l'ensemble des données d'entraînement, et donc plus sujet au surapprentissage, car son espace de recherche est plus grand que celui d'un modèle linéaire.

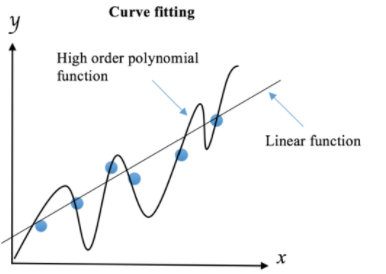
Si un data scientist souhaite doter son chien robot de la capacité à identifier les étrangers en utilisant ses connaissances, il peut utiliser plusieurs méthodes d'apprentissage automatique. Il peut commencer par entraîner un modèle linéaire, car ce type de modèle est souvent préférable en termes de généralisation sur de nouveaux points de données. Pour éviter les effets négatifs des ordres élevés du polynôme, il peut utiliser des techniques de régularisation pour réduire leur influence en imposant des pénalités. Cela permettrait de décourager la complexité et d'obtenir une règle moins précise mais plus robuste apprise à partir des données d'apprentissage.

Sexe	Jeune	Haut	Avec des lunettes	Couleurs
Femelle	Milieu	Moyenne	Avec des lunettes	En noir	Étranger

Si le robot utilise ces règles pour identifier les étrangers, il pourrait conclure que toute femme d'âge moyen de taille moyenne sans lunettes et vêtue de noir est une étrangère, ainsi que tout homme senior de petite taille sans lunettes et vêtu de noir. Le robot pourrait également identifier quelqu'un d'autre comme étant son ami. Cependant, bien que ces règles soient parfaitement conformes aux données d'entraînement, elles sont trop compliquées pour bien généraliser à de nouveaux visiteurs. Pour éviter le surapprentissage, il est recommandé de limiter la complexité du modèle en utilisant des techniques de régularisation et en arrêtant prématurément la procédure d'apprentissage. La régularisation doit être maintenue à un niveau optimal pour éviter un sous-ajustement ou une déviation excessive du modèle par rapport à la vérité.

Sélection de caractéristiques et à la réduction de la dimensionnalité

Les données sont généralement représentées sous forme de matrice où chaque colonne représente une fonctionnalité, également appelée variable, et chaque ligne représente un exemple qui peut être utilisé pour la formation ou les tests de l'apprentissage supervisé. Ainsi, la dimensionnalité des données correspond au nombre de fonctionnalités. Les données de texte et d'image ont généralement une grande dimensionnalité, tandis que les données boursières ont une dimensionnalité relativement faible.

La sélection de fonctionnalités est un processus important pour la construction d'un modèle de qualité. Elle consiste à sélectionner un sous-ensemble de fonctionnalités pertinentes pour l'entraînement du modèle, tout en supprimant les fonctionnalités redondantes ou non pertinentes. La sélection de fonctionnalités implique des décisions binaires pour l'inclusion ou l'exclusion d'une fonctionnalité. Cela peut donner lieu à un grand nombre d'ensembles de fonctionnalités possibles, allant jusqu'à 2^x pour x fonctionnalités.

Pour éviter cette explosion combinatoire, des algorithmes de sélection de caractéristiques plus avancés ont été développés pour identifier les signaux les plus utiles et ainsi réduire la dimensionnalité des données. Ces algorithmes permettent de sélectionner les ensembles de fonctionnalités les plus pertinents de manière plus efficace.

Prétraitement des données et ingénierie des fonctionnalités

Cross-Industry Standard Process for Data Mining (CRISP-DM) :

La prise en charge par des experts spécialisés dans le domaine est importante pour la compréhension commerciale et la compréhension des données, car ils ont une connaissance approfondie du domaine et peuvent contribuer à la définition du problème commercial ainsi qu'à la compréhension des données.

La préparation des données nécessite des compétences techniques pour créer des ensembles de données d'entraînement et de test, et un expert du domaine qui ne maîtrise que Microsoft Excel pourrait ne pas être suffisant pour cette phase.

La modélisation implique la formulation d'un modèle et l'adaptation des données en fonction de celui-ci.

L'évaluation est importante pour déterminer dans quelle mesure le modèle s'adapte aux données, ce qui permet de vérifier si le problème commercial a été résolu de manière satisfaisante.

Le déploiement consiste à configurer le système dans un environnement de production, afin que le modèle puisse être utilisé pour résoudre le problème commercial.

Prétraitement

Le nettoyage des données est une étape essentielle dans le processus de machine learning. Pour nettoyer les données, il est nécessaire de comprendre les données elles-mêmes. Pour ce faire, il est possible d'analyser et de visualiser les données, en fonction de leur type.

Dans le cas d'une table de nombres, il est important de vérifier s'il y a des valeurs manquantes, comment les valeurs sont distribuées et quel type de caractéristiques nous avons. Les valeurs peuvent suivre différents types de distributions, telles que la distribution normale, binomiale, de Poisson ou autre. Les caractéristiques peuvent être binaire (oui ou non, positif ou négatif, etc.), catégoriques (continent d'appartenance, etc.) ou ordonnées (élevé, moyen, faible). Les caractéristiques peuvent également être quantitatives (température en degrés ou prix en dollars).

Lorsque des valeurs manquantes sont détectées, il est important de décider comment les traiter. Il est possible d'ignorer ces valeurs manquantes, mais cela peut entraîner des erreurs de résultats. Il est également possible d'imputer les valeurs manquantes en utilisant la moyenne arithmétique, la médiane ou le mode des valeurs valides d'une certaine caractéristique.

Encodage des étiquettes

Pour que le machine learning fonctionne, il est impératif que les données soient sous forme numérique. Si l'on fournit une chaîne de caractères telle qu'"Ivan", le programme ne pourra pas traiter les données à moins d'utiliser un logiciel spécialisé. Afin de convertir une chaîne de caractères en une valeur numérique, il est possible de :

Étiqueter	Étiquette codée
Afrique	1
Europe	2
Amérique du Sud	3
Amérique du Nord	4
Autre	6

Cette méthode peut causer des problèmes dans certains cas, car l'algorithme d'apprentissage peut en déduire un ordre implicite (à moins qu'un ordre explicite soit attendu, par exemple, mauvais=0, ok=1, bon=2, excellent=3). Dans le tableau de mappage précédent, l'encodage ordinal montre une différence de 4 entre l'Asie et l'Amérique du Nord, ce qui est contre-intuitif car il est difficile de quantifier ces valeurs. Pour remédier à cela, l'encodage One-hot peut être utilisé. Cette méthode utilise des variables fictives pour encoder les caractéristiques catégorielles.

Les variables fictives sont des variables binaires, représentées sous forme de bits, qui prennent des valeurs soit 0 soit 1. Par exemple, pour encoder les continents, nous utiliserions des variables fictives telles que "is_asia", qui seraient vraies si le continent est l'Asie et fausses dans le cas contraire. Le nombre de variables fictives nécessaires est égal au nombre d'étiquettes uniques, moins une. Nous pouvons déduire automatiquement l'une des étiquettes à partir des variables fictives car celles-ci sont mutuellement exclusives. Si toutes les variables fictives sont fausses, l'étiquette correcte sera celle pour laquelle il n'y a pas de variable fictive.

Étiqueter	IsAfrique	Is_asia	Is_Afrique	Is_Europe	Is_sam	Is_nam
Afrique	1	0	0	0	0	0
Europe	0	0	1	0	0	0
Amérique du Sud	0	0	0	1	0	0
Amérique du Nord	0	0	0	0	1	0

Lorsque nous utilisons l'encodage One-hot pour encoder les données catégorielles, cela produit une matrice avec un grand nombre de zéros (représentant des valeurs fausses) et un petit nombre de valeurs non nulles (représentant des valeurs vraies). Cette matrice est appelée matrice creuse car la plupart de ses éléments sont nuls.

Mise à l'échelle

Il est fréquent que les valeurs des différentes fonctionnalités diffèrent par des ordres de grandeur, ce qui peut parfois signifier que les valeurs les plus élevées dominent les valeurs les plus petites. Dans de tels cas, il existe plusieurs stratégies pour normaliser les données :

• La normalisation consiste à soustraire la moyenne de la fonctionnalité et à diviser par l'écart type. Si les valeurs de la fonctionnalité sont normalement distribuées, la fonctionnalité normalisée sera centrée autour de zéro avec une variance de un, formant une distribution gaussienne.

• Si les valeurs des fonctionnalités ne sont pas normalement distribuées, nous pouvons utiliser la médiane et l'intervalle interquartile (IQR) pour normaliser. L'IQR est la différence entre le premier et le troisième quartile (ou le 25e et le 75e centile).

• Une autre stratégie courante est de mettre à l'échelle les fonctionnalités dans une plage allant de zéro à un. Cette méthode est souvent utilisée pour normaliser les données de manière à ce qu'elles soient comparables entre elles. Nous aborderons cette méthode dans nos exemples futurs.

Ingénierie des fonctionnalités

Le processus de création ou d'amélioration des fonctionnalités est souvent basé sur le bon sens, la connaissance du domaine ou l'expérience antérieure. Cependant, il n'y a aucune garantie que la création de nouvelles fonctionnalités améliorera les résultats. Il existe plusieurs techniques pour créer de nouvelles fonctionnalités :

• Transformation polynomiale : si deux caractéristiques ont une relation polynomiale, comme a2 + ab + b2, chaque terme peut être considéré comme une fonctionnalité. L'interaction, telle que ab, peut être une somme, une différence ou un rapport plutôt qu'un produit, et le nombre de caractéristiques et l'ordre du polynôme ne sont pas limités. Cependant, les relations polynomiales complexes peuvent être difficiles à calculer et peuvent conduire à un surajustement.

• Transformation de puissance : les fonctions de transformation peuvent être utilisées pour ajuster les caractéristiques numériques à une distribution normale. Par exemple, le logarithme est une transformation courante pour les valeurs qui varient par ordre de grandeur. La transformation de Box-Cox peut être utilisée pour trouver la meilleure puissance pour transformer les données en une distribution plus proche de la normale.

• Binning : les valeurs des caractéristiques peuvent être regroupées dans plusieurs bacs. Par exemple, si nous ne sommes intéressés que par savoir s'il a plu un jour donné, nous pouvons binariser les valeurs de précipitations afin d'obtenir une valeur vraie si la valeur de précipitations est non nulle, et une valeur fausse sinon.

Combinaison de modèles

En utilisant plusieurs modèles pour produire des prédictions, on peut améliorer la performance globale en réduisant les erreurs individuelles de chaque modèle. Cependant, il est important de trouver un équilibre entre la complexité des modèles et leur capacité à améliorer les résultats.

Le voting et l'averaging sont deux méthodes simples pour combiner les prédictions de plusieurs modèles. Ils sont souvent utilisés lorsque les modèles ont des performances similaires, mais peuvent également être pondérés pour donner plus de poids à des modèles plus fiables. Cependant, il convient de noter que cette approche peut ne pas fonctionner si les modèles sont très différents ou si l'un d'eux est beaucoup moins fiable que les autres.

Le bagging est une technique plus avancée qui peut réduire les risques de surajustement et améliorer la stabilité des prédictions. Elle implique de créer plusieurs ensembles de données d'apprentissage en échantillonnant les données avec remplacement, et de former un modèle pour chaque ensemble. Les résultats des différents modèles sont ensuite combinés pour produire une prédiction finale. Cette technique peut être particulièrement utile pour les modèles qui ont tendance à surajuster les données d'apprentissage.

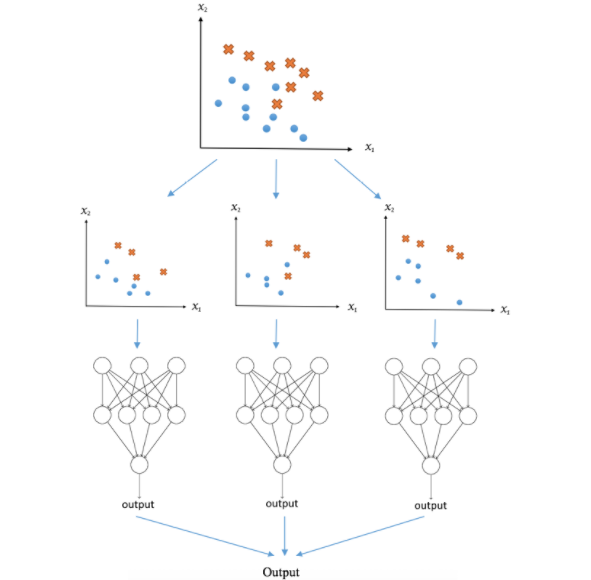
En fin de compte, le choix de la technique de combinaison dépendra des caractéristiques du modèle et des données, ainsi que des objectifs spécifiques du projet. Il est important de considérer plusieurs modèles et techniques de combinaison pour obtenir les meilleurs résultats possibles.