Description

Les graphes sont des structures informatiques utilisées dans notre vie de tous les jours :

• Les villes qui s'interconnectent
• Nos réseaux sociaux qui nous connectent les uns aux autres
• Des pages webs

Et bien d'autres cas qui représente des liens entre différents acteurs. Ces graphes ont permis à travers les ages, l'élaboration d'algorithmes visant à solutionner des cas complexes.

Prérequis Avant de commencer nous allons utiliser l'un des languages les plus utilisés dans le monde du machine learning : Python.

Voici les liste des éléments utilisés dans notre exercice :

Jupyter==1.0.0 networkx==2.5 snap-stanford==5.0.0 matplotlib==3.2.2 pandas==1.1.3 scipy==1.6.2

Networkx va nous permettre d'illuster la théorie des graphes à travers divers exemples.

Graphe simple non orienté

Un graphe non orienté (G) est définit par un ensemble de Sommets (V) et d'arêtes (E) ou liens interconnectant les sommets.

Ainsi nous pouvons dire qu'un Graph est représenté mathématiquement comme : G = (V,E) où V est représenté par un ensemble de sommets V={ V1, .., Vn} qui sont connecté par un ensemble d'arêtes qui définit les liens entre chaque sommet E= {{Vk, Vi} ... {Vi,Vn}}.

Dans le cas d'un graphe non-orienté, l'ordre des arêtes défini n'a pas d'importance, ainsi : {Vk, Vn} et {Vn, Vk} désigne la même arete (lien).

Donc retenons nos premières formules :

• G= (V, E)
• V={ V1, .., Vn}
• E= {{Vk, Vi} ... {Vi,Vn}} où l'ensemble des liens n'est pas orienté

La théorie des graphes nous permet aussi de définir :

• L'ordre : nombre de sommets (V) d'un graph.
• La taille : nombre d'aretes (E) d'un graph.
• Le degré d'un sommet : nombre d'aretes qui lui sont adjacentes.
• Les voisin d'un sommet : Sous ensemble de sommet V' induit par tous les sommets adjacents
• Le graphe de voisinage (ego) est un sous graphe de G, composé des sommets et aretes adjacentes à V.

Exemple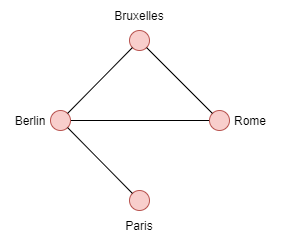

Dans le cas d'un graph non orienté les aretes reliant Berlin à Paris {Berlin, Paris} sont égales à {Paris, Berlin} il n'existe aucune distinction entre ces deux aretes.

• Ordre: 4 car nous avons 4 sommets (Berlin, Bruxelles, Paris, Rome)
• Degrée de Bruxelles, Rome : 2
• Degrée de Berlin : 3
• Degrée de Paris: 1

Les voisins de chaque sommets :

• Paris={Berlin}
• Berlin={Bruxelles, Rome, Paris}
• Bruxelles={Rome, Berlin}
• Rome={Bruxelles, Berlin}

Pour illustrer cet example nous avons besoin de créer un grah non-orienté, pour ce faire : nx.Graph() nous permet de créer ce type de graph sans spécifier un sens. Cette méthode retourne un objet où tout les sommets et aretes sont accessible. Voici quelque méthodes utiles :

| Fonction | Description | Type de retour | |---|---|---| | Graph() | Retourne un graphe non orienté | Graph | | Graph.number_of_edges() | Retourne le nombre d'aretes | Number | | Graph.number_of_nodes() | Retourne le nombre de sommets| Number | | Graph.degree() | Retourne un tableau représentant le degré de chaque sommet| Array | | Graph.neighbors() | Retourne un tableau représentant les sommets et chacun de leurs voisins | Array | | Graph.ego_graph( Graph G, String nameOfGraph) | Retourne le sous graph voisin | Array | | Graph.add_nodes_from(V) | Ajoutes des sommets | void | | Graph.add_edges_from(E) | Ajoutes des aretes | void | | Graph.remove_nodes_from(V) | Supprimes des sommets | void | | Graph.remove_edges_from(E) | Supprimes des arêtes | void |

import networkx as nx

G = nx.Graph() V = {'Dublin', 'Paris', 'Milan', 'Rome'} E = [('Milan','Dublin'), ('Milan','Paris'), ('Paris','Dublin'), ('Milan','Rome')] G.add_nodes_from(V) G.add_edges_from(E)

print(f"V = {G.nodes}") print(f"E = {G.edges}") print(f"Graph Order: {G.number_of_nodes()}") print(f"Graph Size: {G.number_of_edges()}") print(f"Degree for nodes: { {v: G.degree(v) for v in G.nodes} }") print(f"Neighbors for nodes: { {v: list(G.neighbors(v)) for v in G.nodes} }")

Resultat :

V = ['Paris', 'Rome', 'Bruxelles', 'Berlin'] E = [('Paris', 'Berlin'), ('Rome', 'Berlin'), ('Rome', 'Bruxelles'), ('Bruxelles', 'Berlin')] Graph Order: 4 Graph Size: 4 Degree for nodes: {'Berlin': 3, 'Paris': 1, 'Bruxelles': 2, 'Rome': 2} Neighbors for nodes: {'Berlin': ['Rome', 'Paris', 'Bruxelles'], 'Paris': ['Berlin'], 'Bruxelles': ['Rome', 'Berlin'], 'Rome': ['Berlin', 'Bruxelles']}

Nous pouvons également calculer un graphe d'ego d'un sommet spécifique pour le graphe G :

ego_graph_berlin = nx.ego_graph(G, "Berlin")

print(f"Nodes: {ego_graph_berlin.nodes}") print(f"Edges: {ego_graph_berlin.edges}")

Resultat :

Nodes: ['Paris', 'Milan', 'Dublin', 'Rome'] Edges: [('Paris', 'Milan'), ('Paris', 'Dublin'), ('Milan', 'Dublin'), ('Milan', 'Rome')]

Graphe simple orienté (digraphs)

Un graphe orienté (G) est définit par un ensemble de Sommets (V) et d'arêtes (E) ou liens interconnectant les sommets.

Ainsi nous pouvons dire qu'un Graph est représenté mathématiquement comme : G = (V,E) où V est représenté par un ensemble de sommets V={ V1, .., Vn} qui sont connecté par un ensemble d'arêtes qui définit les liens entre chaque sommet E= {{Vk, Vi} ... {Vi,Vn}}.

Dans le cas d'un graphe orienté, l'ordre des arêtes défini a une importance, ainsi : {Vk, Vn} et {Vn, Vk} ne désigne pas la même arête. {Vk, Vn}: Cela signifie que Vk va vers Vn et que Vn pourrait ne pas aller vers Vk si on ne le stipule pas.

Ainsi nous étendons le degré à un type de dégré intérieur et extérieux :

• deg-(v): Pour un sommet V, c'est le nombre de têtes adjacents à v
• deg+(v): Pour un sommet V, c'est le nombre de queue adjacents à v

Exemple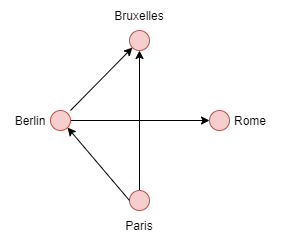

• deg-(v) de Bruxelles: 2
• deg+(v) de Bruxelles: 0
• deg-(v) de Paris: 0
• deg+(v) de Paris: 2
• deg-(v) de Rome: 1
• deg+(v) de Rome: 0
• deg-(v) de Berlin: 1
• deg+(v) de Berlin: 2

Voici quelque méthodes utiles pour le digraph :

| Fonction | Description | Type de retour | |---|---|---| | DiGraph() | Retourne un digraph | DiGraph | | DiGraph.in_degree() | Retourne un tableau avec le degré intérieur par sommet | array | | DiGraph.out_degree() | Retourne un tableau avec le degré extérieur par sommet | array |

Testons ceci :

import networkx as nx

G = nx.DiGraph() V = {'Dublin', 'Paris', 'Milan', 'Rome'} E = [('Milan','Dublin'), ('Paris','Milan'), ('Paris','Dublin'), ('Milan','Rome')] G.add_nodes_from(V) G.add_edges_from(E)

print(f"Indegree for nodes: { {v: G.in_degree(v) for v in G.nodes} }") print(f"Outdegree for nodes: { {v: G.out_degree(v) for v in G.nodes} }")

Resultat :

Indegree for nodes: {'Paris': 0, 'Dublin': 2, 'Milan': 1, 'Rome': 1} Outdegree for nodes: {'Paris': 2, 'Dublin': 0, 'Milan': 2, 'Rome': 0}

Multigraphe

C'est une généralisation du graphe qui permet à plusieurs arêtes d'avoir la même paire d'arêtes.

• C'est un graphe orienté si E est un multi ensemble de couples ordonnés
• C'est un graphe non orienté dans le cas où E est un multi-ensemble de deux-ensembles

Mutligraphe orienté :

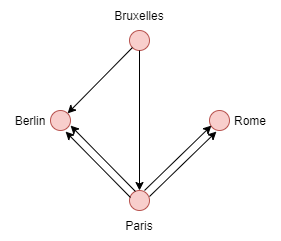
Voici quelque méthodes utiles pour le multigraphe:

| Fonction | Description | Type de retour | |---|---|---| | MultiDiGraph() | Retourne un multigraph orienté | MultiDiGraph | | MultiGraph.in_degree() | Retourne un multigraph non orienté | MultiGraph |

import networkx as nx

directed_multi_graph = nx.MultiDiGraph() undirected_multi_graph = nx.MultiGraph() V = {'Dublin', 'Paris', 'Milan', 'Rome'} E = [('Milan','Dublin'), ('Milan','Dublin'), ('Paris','Milan'), ('Paris','Dublin'), ('Milan','Rome'), ('Milan','Rome')] directed_multi_graph.add_nodes_from(V) undirected_multi_graph.add_nodes_froms/span>(V) directed_multi_graph.add_edges_from(E) undirected_multi_graph.add_edges_from(E)

Graphiques pondérés

Un graphe pondéré (G) est définit par un ensemble de Sommets (V) et d'arêtes (E) ou liens interconnectant les sommets et inclus une fonction pondérées qui accorde à chaque arête un poid exprimé en chiffre.

Ainsi nous pouvons dire qu'un Graph pondéré est représenté mathématiquement comme : G = (V,E, w) où V est représenté par un ensemble de sommets V={ V1, .., Vn} qui sont connecté par un ensemble d'arêtes qui définit les liens entre chaque sommet E= {{Vk, Vi} ... {Vi,Vn}} et dont les arêtes on une fonction pondérée attribuant un poid w: V -> R.

A savoir :

• Si E est un ensemble de couples ordonné: graphe orienté pondéré
• Si E est un ensemble de deux ensembles: graphe pondéré non orienté
• Si E est un multi-ensemble: multigraphe pondéré ( multigraphe pondéré dirigé )
• Si E est un ensemble de couples ordonné: graphe orienté pondéré

Exemple

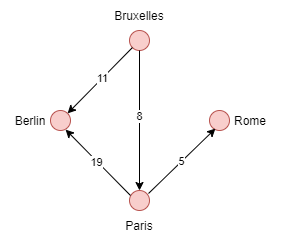
On estime le poid d'une arête comme un coup atteindre un sommet. Dans le cas présent pour que Bruxelles atteigne Berlin cela couterait 11.

import networkx as nx

G = nx.DiGraph() V = {'Dublin', 'Paris', 'Milan', 'Rome'} E = [('Milan','Dublin', 19), ('Paris','Milan', 8), ('Paris','Dublin', 11), ('Milan','Rome', 5)] G.add_nodes_from(V) G.add_weighted_edges_from(E)

Graphiques bipartites

Ce sont des graphes multiparties comme : bipartites, tripartites ou kth-partite qui sont des graphes dont les sommets peuvent être partitionnés en deux, trois ou Xieme ensemble de sommets.

Cas d'utilisations :

• Lors du traitement des documents et de la structuration des informations dans un graphe bipartite des documents et entités qui apparaissent dans les documents
• Lorsqu'il s'agit de données transactionnelles, afin d'encoder les relations entre les acheteurs et les commerçants

Exemple

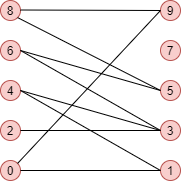
import networkx as nx import pandas as pd import numpy as np

n_nodes = 10 n_edges = 12 bottom_nodes = [ith for ith in range(n_nodes) if ith % 2 ==0] top_nodes = [ith for ith in range(n_nodes) if ith % 2 ==1] iter_edges = zip( np.random.choice(bottom_nodes, n_edges), np.random.choice(top_nodes, n_edges)) edges = pd.DataFrame([ {"source": a, "target": b} for a, b in ter_edges]) B = nx.Graph() B.add_nodes_from(bottom_nodes, bipartite=0) B.add_nodes_from(top_nodes, bipartite=1) B.add_edges_from([tuple(x) for x in edges.values])

matrice d'adjacence

Une matrice adjacente permet de créer une meilleure représentativité d'un graphe. Ainsi une matrice M d'un graphe G = (V,E) est une matrice carré des sommets (|V| x |V|) tel que Mij est égal à 1 si une arête relie I à J et 0 dans le cas contraire.

Exemple

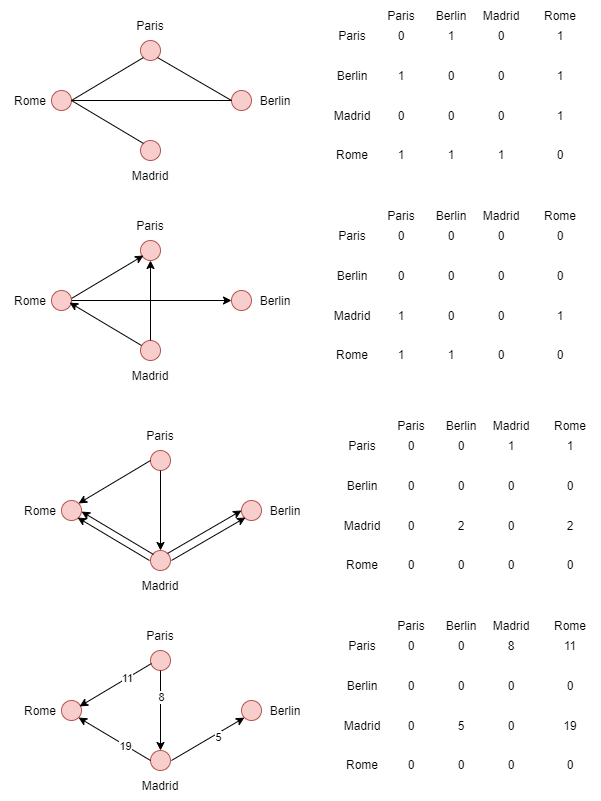
• Pour les graphes nonorientés on peut remarqué que le poid s'applique à chacun des sommets.
• Pour les graphes orientés (bigraphe) on peut remarqué que le poid s'applique au sommet de départ.
• Pour les multigraphes on remarque que la valeur change à partir du moment où plusieurs arêtes pointent vers un même sommet.
• Pour les graphes pondéré on remarque que chaque valeur de la matrice à un poid supérieur en fonction du poid défini par l'arête.

métriques

Chaque graphe représente un réseau d"une taille donnée par : le nombre de sommets et d'arêtes. Mais ces données ne sont pas suffisantes pour cela il existe 4 types de métriques :

• Métriques d'intégration: Mesure comment chaque sommet sont interconnectés les uns aux autres
• Métriques de ségrégation: Quantifie la présence de groupes de sommets qui sont connectés les uns aux autres (modules)
• Métriques de centralité: Evalue l'importance des sommets individuels
• Métriques de résilience: Mesure la capacité d'un réseau à maintenir et adapter ses performances opérationnelles face à des pannes.

Métriques d'intégration

Parlons du concepte de distance : il est lié au nombre d'arêtes à parcourir pour atteindre un sommet donné. On a dès lors :

• Un sommet de départ I
• Un sommet d'arrivé J
• Le chemin (l'ensemble des arêtes entre les deux sommets) le plus court (moins d'arêtes).
• Le diamètre (le nombre d'arêtes dans le chemin le plus court)

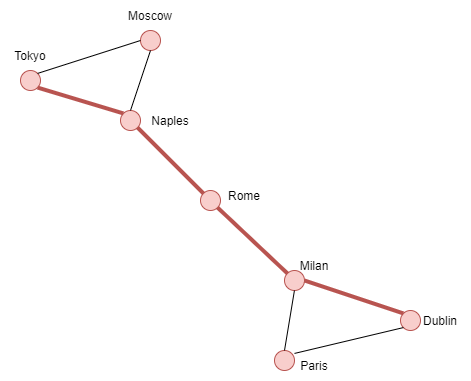
Chemin le plus court

| Fonction | Description | Type de retour | |---|---|---| | shortest_path(Graph, Number source, Number target) | Retourne les chemin le plus court d'un graphe | Array |

Exemple:

import networkx as nx

G = nx.Graph() nodes = {1:'Dublin',2:'Paris',3:'Milan',4:'Rome',5:'Naples', 6:'Moscow',7:'Tokyo'} G.add_nodes_from(nodes.keys()) G.add_edges_from([(1,2),(1,3),(2,3),(3,4),(4,5),(5,6),(6,7),(7,5)]) path = nx.shortest_path(G,source=1,target=7)

Résultat:

[1,3,4,5,6]

Longueur du chemin

Pour calculer la longueur du trajet :

• Li est la longueur moyenne du chemin entre 2 noeuds
• V est l'ensemble des sommets
• q = |V| représente l'ordre

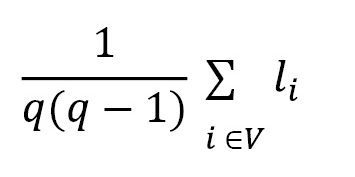
| Fonction | Description | Type de retour | |---|---|---| | average_shortest_path_length(Graph) | Retourne la longueur du chemin | Float |

Attention: Il n'est pas toujours possible de calculer un chemin parmi tous les sommets qui ne sont pas connecté.

import networkx as nx

nx.average_shortest_path_length(G)

Résultat :

2.1904761904761907

Efficacité globale et locale L'efficacite globale est la moyenne de l'inverse de la longueur du chemin le plus court pour toutes les arêtes. Ainsi :

• Lij est le chemin le plus court entre le sommet i et j

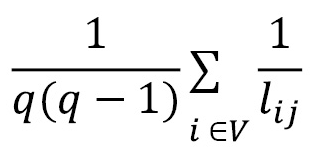
L' efficacité locale d'unnœud peut être calculé en ne considérant que le voisinage du nœud dans le calcul

| Fonction | Description | Type de retour | |---|---|---| | global_efficiency(Graph) | Retourne la longueur du chemin | Float | | local_efficiency(Graph) | Retourne la longueur du chemin | Float |

import networkx as nx

nx.global_efficiency(G) nx.local_efficiency(G)

Résultat:

0.6111111111111109 0.6666666666666667

En conclusion, nous pouvons dire que graphique entièrement connecté est plus efficace qu'un graphique circulaire. En effet dans un graphe entièrement connecté, chaque sommet atteint son objectif plus rapidement par l'utilisation d'autre sommet là où un circulaire aura besoin de passer par tout les autres sommets :

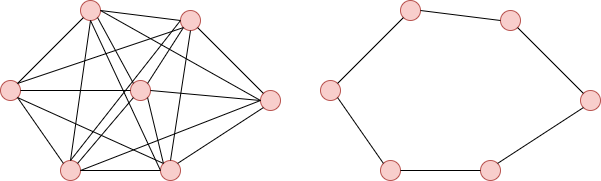
Métriques de ségrégation

Coefficient de regroupement

Permet de mesurer le nombre de sommet regrouper. Il est définit comme des triangles (3 sommets et trois arêtes) autour d'un sommet et équivaut à la fractions de sommets voisins.

| Fonction | Description | Type de retour | |---|---|---| | average_clustering(Graph) | Retourne la moyenne du voisinage | Float | | clustering(Graph) | Retourne le voisinage | Object |

import networkx as nx

nx.average_clustering(G) nx.clustering(G)

Résultat :

0.6666666666666667

{1: 1.0, 2: 1.0, 3: 0.3333333333333333, 4: 0, 5: 0.3333333333333333, 6: 1.0, 7: 1.0}

Modularité Permet de quantifier la division d'un résean en un ensemble de sommets interconnectés (ou modules, clusters,...). L'idée principale est que les réseaux ayant une modularité élevée afficheront des connexions denses au sein du module et des connexions clairsemées entre les modules.

Envisagez un social réseau tel que Reddit : les membres des communautés liées aux jeux vidéo ont tendance à interagir beaucoup plus avec les autres utilisateurs de la même communauté, en parlant des dernières nouvelles, des consoles préférées, etc. Cependant, ils interagiront probablement moins avec les utilisateurs qui parlent de mode. Contrairement à de nombreuses autres métriques de graphes, la modularité est souvent calculée au moyen d'algorithmes d'optimisation.

Les mesures de ségrégation aident à comprendre la présence de groupes. Cependant, chaque sommet d'un graphe a sa propre importance . Pour le quantifier, nous pouvons utiliser des métriques de centralité.

| Fonction | Description | Type de retour | |---|---|---| | modularity(Graph, Array communities) | Retourne la modularité | Float |

Communities est une liste d'ensembles, chacun représentant une partition du graphe.

import networkx.algorithms.community as nx_comm

nx_comm.modularity(G, communities=[{1,2,3}, {4,5,6,7}])

Résultat

0.3671875

Métriques de centralité

Centralité du sommet Cette centralité est lié au degré d'un sommet, mesurant le nombre d'arêtes sur un certain sommet. Plus un sommet est connecté à un autre, plus son degré de centralité prendra de la valeur.

| Fonction | Description | Type de retour | |---|---|---| | degree_centrality(Graph) | Retourne la centralité de chaque sommet | Object |

import networkx as nx

nx.degree_centrality(G)

Résultat:

{1: 0.3333333333333333, 2: 0.3333333333333333, 3: 0.5, 4: 0.3333333333333333, 5: 0.5, 6: 0.3333333333333333, 7: 0.3333333333333333}

Centralité de proximité Cette métrique permet de quantifier à quel point un sommet est connecté (proche) d'un autre :

• I représente la distance moyenne entre les autres sommets
• V est l'ensembre des sommets
• Si Lij est le chemin le plus court entre i et j, la centralité est définie :

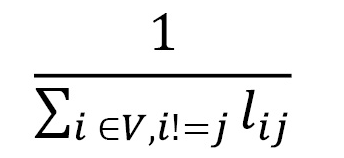
| Fonction | Description | Type de retour | |---|---|---| | closeness_centrality(Graph) | Retourne la proximité de chaque sommet | Object |

import networkx as nx

nx.closeness_centrality(G)

Résultat:

{1: 0.4, 2: 0.4, 3: 0.5454545454545454, 4: 0.6, 5: 0.5454545454545454, 6: 0.4, 7: 0.4}

Centralité d'intermédiation Elle évalue dans quelle mesure un sommet agit comme un pont entre d'autre sommets du graphe, à savoir que même mal connecté un sommet peut être connecté.

• Lwj est le nombre total de chemin les plus courts entre w et j
• Lwj(i) est le nombre total de chemins les plus courts entre w et j, mais passant par i

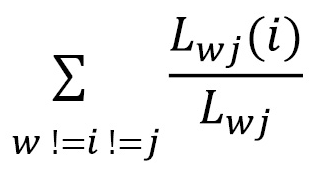
| Fonction | Description | Type de retour | |---|---|---| | betweenness_centrality(Graph) | Retourne la centralité intermédaire de chaque sommet | Object |

import networkx as nx

nx.betweenness_centrality(G)

Résultat:

{1: 0.0, 2: 0.0, 3: 0.5333333333333333, 4: 0.6, 5: 0.5333333333333333, 6: 0.0, 7: 0.0}

Métriques de résilience

Centralité d'assortativité C'est l'hatitude à quantifier la tendance des sommets à être connectés à des sommets similaires. Coefficient de corrélation de Pearson entre les sommets :

• le coefficient prend des valeurs positives lorqu'il existe une corrélation entre les sommets de degré similaire.
• le coefficient prend des valeurs négatives lorsqu'il existe une corrélation entre des sommets de degré différent.

| Fonction | Description | Type de retour | |---|---|---| | degree_pearson_correlation_coefficient(Graph) | Retourne la centralité d'assortativité| float |

import networkx as nx

nx.degree_pearson_correlation_coefficient(G)

Résultat:

-0.6

Mise en pratique

La théorie est maintenant apprise, il nous faut des cas concrets afin d'illuster notre théorie.

graphe non orienté entièrement connecté

Les graphe non orienté représente un élément fondamental qui peut apparaître dans des graphes plus grands. On a un sous-graphe entièrement connecté de n sommets à l'intérieur d'un graphe plus grand : CLIQUE de taille n.

import networkx as nx

nx.complete_graph(n=7)

Une clique C est un sous-ensemble de sommets c C v, tel que : tous les deux sommets distincts du sous-ensemble sont adjacents. Les cliques représentent l'un des concepts de base de la théorie des graphes et sont souvent également utilisées dans des problèmes mathématiques où les relations doivent être codées.

Graphe complete :

C'est un graphe entièrement connecté

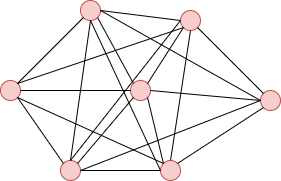
Graphe en sucette :

Il forme une clique de taille n est une branche de m sommets.

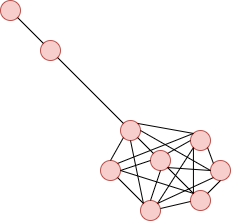
import networkx as nx

nx.lollipop_graph(m=7, n=3)

Graphe d'haltères :

Formé par deux cliques de taille m1 et m2 relié par une branche de sommets.

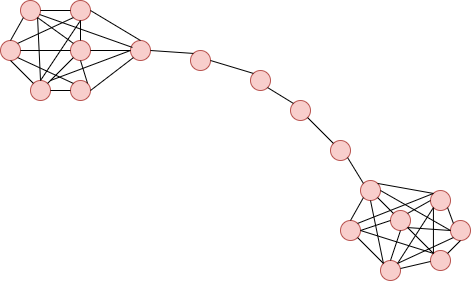
import networkx as nx

nx.barbell_graph(m1=7, m2=4)

Ces graphiques simples sont des blocs de construction de base qui peuvent être utilisés pour générer des réseaux plus complexes en les combinant.