La descente de gradient

Introduction

La descente de gradient est un algorithme qui peut être utilisé pour trouver les valeurs de w et b qui donnent la plus petite valeur possible pour la fonction coût, j, pour la régression linéaire. Il est couramment utilisé dans l'apprentissage automatique, non seulement pour la régression linéaire, mais aussi pour la formation de modèles plus avancés tels que les modèles d'apprentissage profond. La compréhension de la descente de gradient est un élément fondamental de l'apprentissage automatique.

Explication du gradient

Pour créer un gradient, nous avons la fonction coût j de w : 𝐽(𝑤,𝑏), que nous voulons minimiser. 𝐽(𝑤,𝑏) : est une fonction appelée pour la régression linéaire. La descente de gradient n'est pas limitée à la régression linéaire et peut être appliquée à une grande variété de fonctions coût et de modèles qui ont plus de deux paramètres.

Par exemple :

Nous avons une fonction coût : 𝐽(W1, W2,...Wn,𝑏), votre objectif est de minimiser J sur les paramètres. La descente de gradient est un algorithme qui peut être utilisé pour minimiser une fonction coût, 𝐽, en trouvant les valeurs optimales pour les paramètres (W1, W2, ..., Wn) et b. L'algorithme démarre avec des hypothèses initiales pour ces paramètres, qui peuvent être arbitraires. Pour la régression linéaire, il est courant de définir les valeurs initiales des paramètres à 0.

L'algorithme de descente de gradient ajuste les paramètres (W1, W2, ..., Wn) et b de manière itérative pour minimiser la fonction coût, j. L'algorithme continue à mettre à jour les paramètres jusqu'à ce que le coût atteigne un minimum ou un point proche de minimum. Il est important de noter que pour certaines fonctions, il peut y avoir plusieurs points de minimum, pas seulement un. Ce qui signifie que nous avons plus de possibilités qu'une régression linéaire.

Comment mettre en place ? La descente de gradient est un algorithme pour trouver des valeurs de paramètres w et b qui minimisent la fonction coût J. L'algorithme de descente de gradient met à jour les paramètres à chaque étape en soustrayant une petite quantité, déterminée par le taux d'apprentissage alpha, de la valeur actuelle du paramètre. Cette petite quantité est calculée comme la dérivée de la fonction coût par rapport au paramètre, multipliée par le taux d'apprentissage. Plus formalement, à chaque étape, le paramètre w est mis à jour pour prendre la valeur de w moins alpha fois la dérivée de la fonction coût J par rapport à w. Nous pouvons formuler le taux d'apprentissage comme : contrôle de la grandeur du pas que nous allons prendre quand les paramètres, W et B sont mis à jour.

Il est important de garder à l'esprit que l'opérateur d'affectation utilisé en programmation (que vous utilisez tous les jours lors de la programmation) est différent des assertions de vérité en mathématiques.

En programmation, l'opérateur d'égalité est souvent représenté par "==" (par exemple en Python), alors qu'en notation mathématique, le signe égal est utilisé à la fois pour les affectations et les assertions de vérité. Il est important de noter que, en notation mathématique, le signe égal peut avoir des significations différentes en fonction du contexte, telles que l'affectation ou la comparaison.

Parlons du symbole mathématique :

α : Le taux d'apprentissage, noté alpha, est un petit nombre positif compris entre 0 et 1 qui contrôle la taille des pas lors des mises à jour à chaque itération de l'algorithme de descente de gradient. Il est utilisé pour équilibrer le compromis entre la taille des pas et le nombre d'itérations nécessaires pour atteindre la solution optimale. Un choix courant pour le taux d'apprentissage est 0,01.

En s'appuyant sur cela, nous pouvons dire que : le taux d'apprentissage ou alpha, détermine la taille des pas lors des mises à jour des paramètres lors de l'algorithme de descente de gradient. Un taux d'apprentissage élevé correspond à des pas plus importants, ce qui entraîne une recherche plus agressive de la solution optimale. À l'inverse, un taux d'apprentissage faible correspond à des pas plus petits, ce qui entraîne une recherche plus lente mais potentiellement plus précise de la solution optimale.

On peut ajouter le terme de dérivation, qui permet de déterminer quel pas sera le prochain à effectuer, c'est-à-dire le plus petit possible : d/dw X 𝐽(w,b).

Le taux d'apprentissage alpha, avec le terme de dérivation, détermine la taille des pas lors de la descente dans le processus d'optimisation. Il est important de noter que le modèle a deux paramètres, w et b, et que le paramètre b est mis à jour en utilisant une opération d'affectation similaire. Il faut garder à l'esprit que les dérivées viennent du calcul différentiel. B est affecté à l'ancienne valeur de b moins le taux d'apprentissage alpha multiplié par ce terme de dérivation légèrement différent, d/db de J de wb.

Nous pouvons considérer cette formule de cette façon :

𝑤 = 𝑤−𝛼∂𝐽(𝑤,𝑏)∂𝑤
𝑏 = 𝑏−𝛼∂𝐽(𝑤,𝑏)∂𝑏

Pour implémenter correctement la descente de gradient, vous pouvez mettre à jour simultanément les deux paramètres en attribuant les nouvelles valeurs à des variables temporaires temp_w et temp_b. Ces dernières sont calculées en soustrayant les termes de dérivée correspondants aux valeurs actuelles de w et b. J'ai remarqué que la valeur précédente de mise à jour de w est utilisée dans le terme de dérivée pour b.

tmp_w = 𝑤 = 𝑤−𝛼∂𝐽(𝑤,𝑏)∂𝑤

tmp_b = 𝑏 = 𝑏−𝛼∂𝐽(𝑤,𝑏)∂𝑏

Ensuite, les valeurs mises à jour sont attribuées à nouveau à w et b.

w = tmp_w b = tmp_b

Faites attention à suivre ces étapes, changer l'ordre et ne pas attribuer tmp_w et tmp_b en même temps ne sera pas une implémentation correcte. Il assignera de toute façon une valeur incorrecte, déjà mise à jour, à tmp_b et n'appliquera pas la valeur correcte !

Lorsque l'on parle de la descente de gradient, on suppose généralement que les paramètres sont mis à jour simultanément. Cependant, il est possible de mettre à jour les paramètres séparément, mais cette approche n'est pas considérée comme la bonne façon d'implémenter la descente de gradient et serait considérée comme un algorithme différent avec des propriétés différentes. Il est fortement recommandé d'utiliser la méthode de mise à jour simultanée correcte.

Intuition de la descente de gradient Pour le définir et être plus clair, définissons ce graphique :

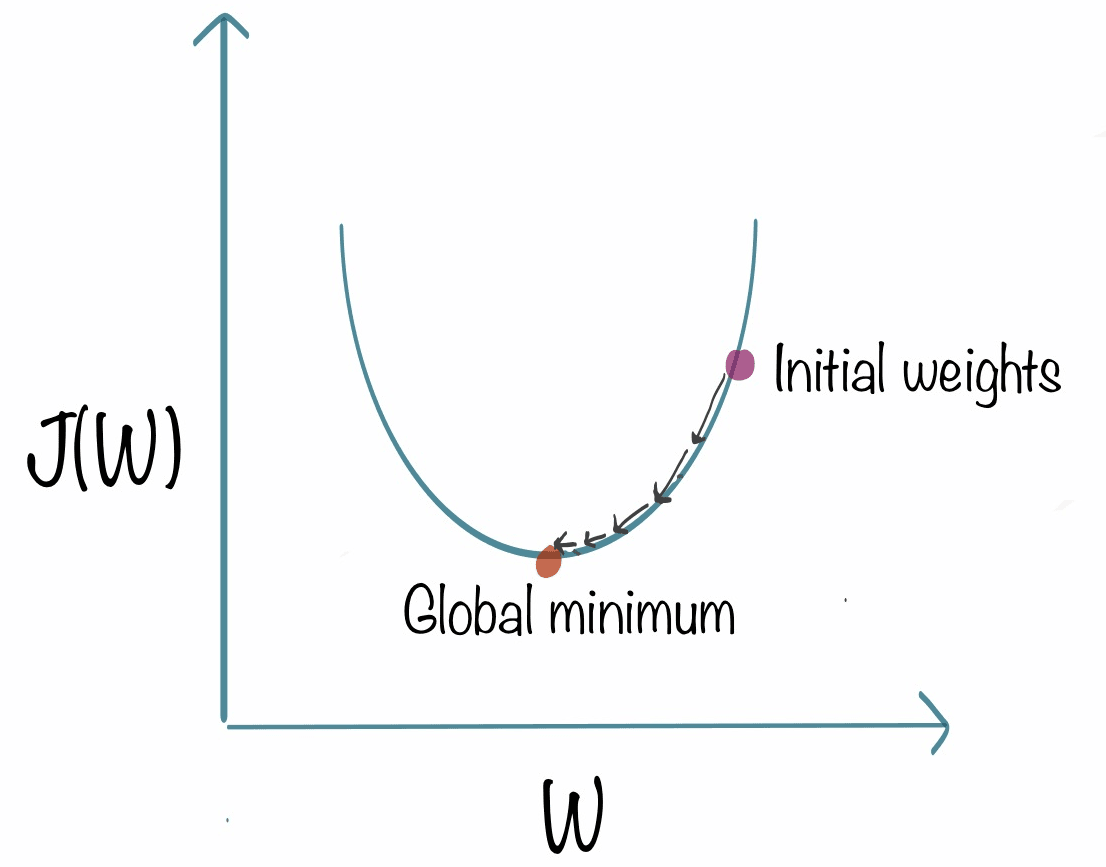
Sur l'axe horizontal, nous avons le paramètre W Sur l'axe vertical, nous avons la fonction coût de W Vous pouvez voir que nous l'avons initialisé sur les poids initiaux, ce que nous allons faire c'est d'appliquer cette formule :

𝑤 = 𝑤−𝛼∂𝐽(𝑤,𝑏)∂𝑤

Une façon de comprendre la dérivée à un point spécifique sur une ligne est de considérer la droite tangente qui touche la courbe à ce point.

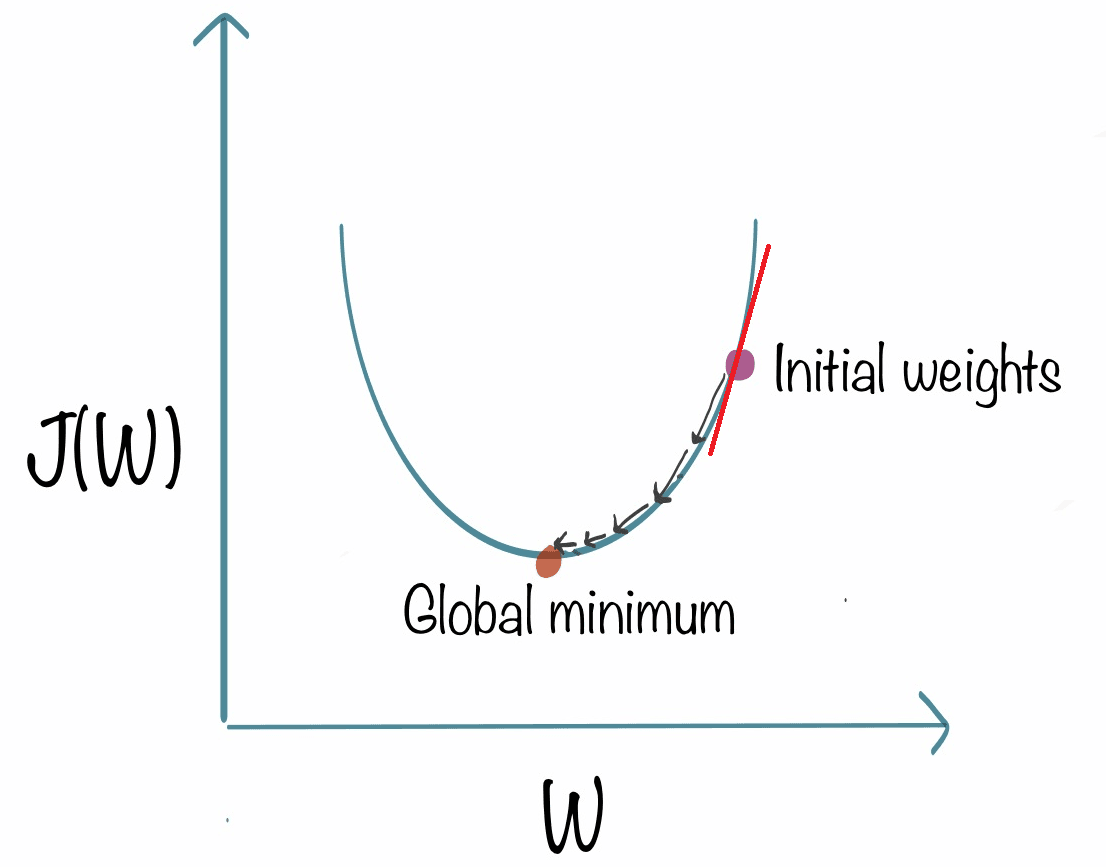
Maintenant, nous avons la pente de cette ligne et c'est la dérivée de la fonction j à ce point. Nous pouvons définir la pente en dessinant comme ceci :

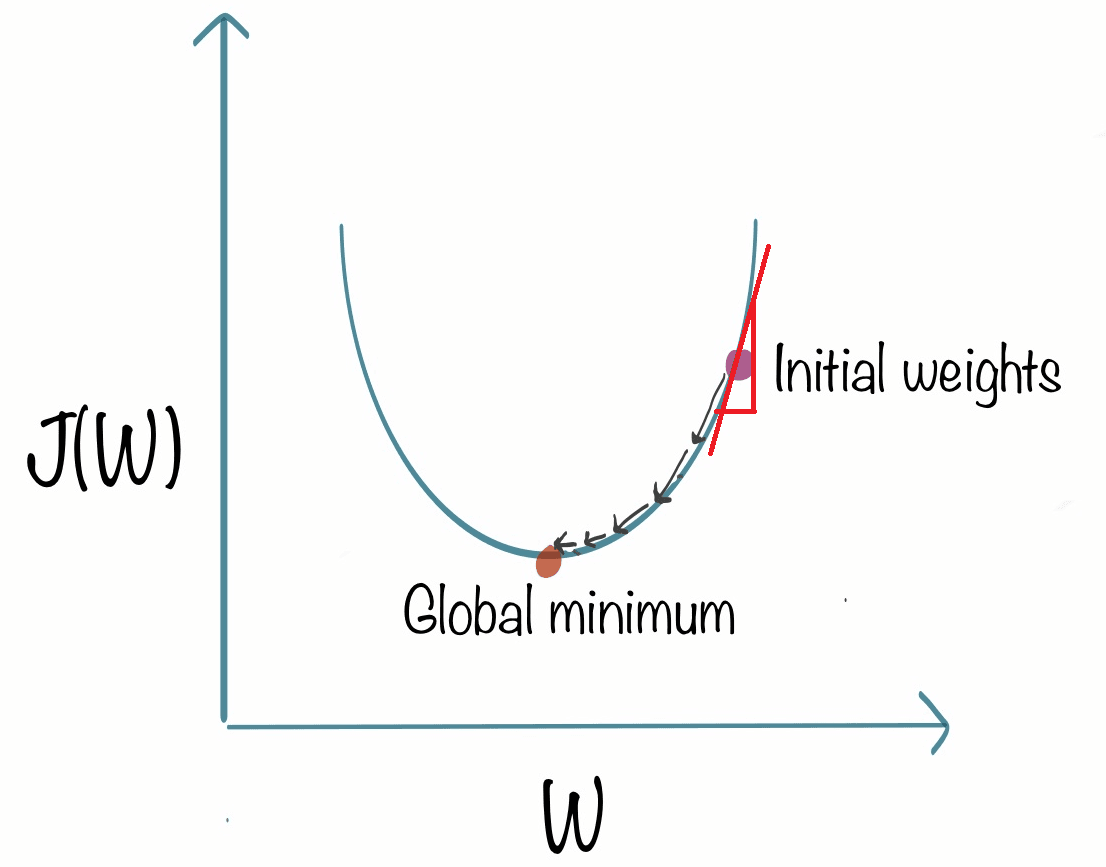
La valeur de la fente est : la hauteur divisée par la largeur du triangle. Ici, disons que c'est 2/1, ce qui donne un résultat positif.

La nouvelle valeur de w est calculée en soustrayant le produit du taux d'apprentissage et d'une valeur positive de la valeur actuelle de w. Comme le taux d'apprentissage est toujours positif, cela entraîne une valeur plus petite pour w. Cela peut être visualisé comme un déplacement vers la gauche sur un graphique, et comme le coût J diminue lorsque nous nous déplaçons vers la gauche sur la courbe, c'est le résultat souhaité car cela nous rapproche de la valeur minimale de J. La descente de gradient fonctionne donc comme prévu. Disons donc :

w = w - ∂ X (nombre positif)

La position où vous commencerez, avec cette formule, sera toujours la même dans ce cas. La différence est : lorsque vous commencerez depuis la gauche du graphique, vous aurez cette formule :

w = w - ∂ X (nombre négatif)

Pourquoi ? Parce que W est le point 0, aller à sa gauche signifie que vous allez à une valeur négative car : hauteur égale -2 et largeur est 1.

Lorsque l'on soustrait un nombre négatif à w, c'est la même chose que d'ajouter un nombre positif à w. Cela entraîne une augmentation de w, qui peut être visualisée comme un déplacement vers la droite sur un graphique. Comme le coût J diminue lorsque nous nous déplaçons vers la droite sur la courbe, c'est le résultat souhaité car cela nous rapproche de la valeur minimale de J. Ainsi, la descente de gradient fonctionne comme prévu. Dans chaque cas, nous aidons à nous rapprocher de la valeur minimale de W.

Donc quand:

Nous avons un nombre positif : nous diminuons W Nous avons un nombre négatif : nous augmentons W

Learning rate

La valeur de la vitesse d'apprentissage, alpha, joue un rôle crucial dans les performances de la descente de gradient. Si alpha n'est pas choisi correctement, la descente de gradient peut ne pas fonctionner correctement ou pas du tout. Comprendre les effets d'alpha peut aider à sélectionner une valeur appropriée pour les futures implémentations de la descente de gradient. La règle de descente de gradient met à jour w de la manière suivante: w = w - (alpha * dérivée). Si la vitesse d'apprentissage, alpha, est soit trop petite soit trop grande, cela peut affecter les performances du modèle.

Prenez notre formule:

𝑤 = 𝑤−𝛼∂𝐽(𝑤,𝑏)∂𝑤

Pour illustrer les explications à venir, nous prendrons cette image :

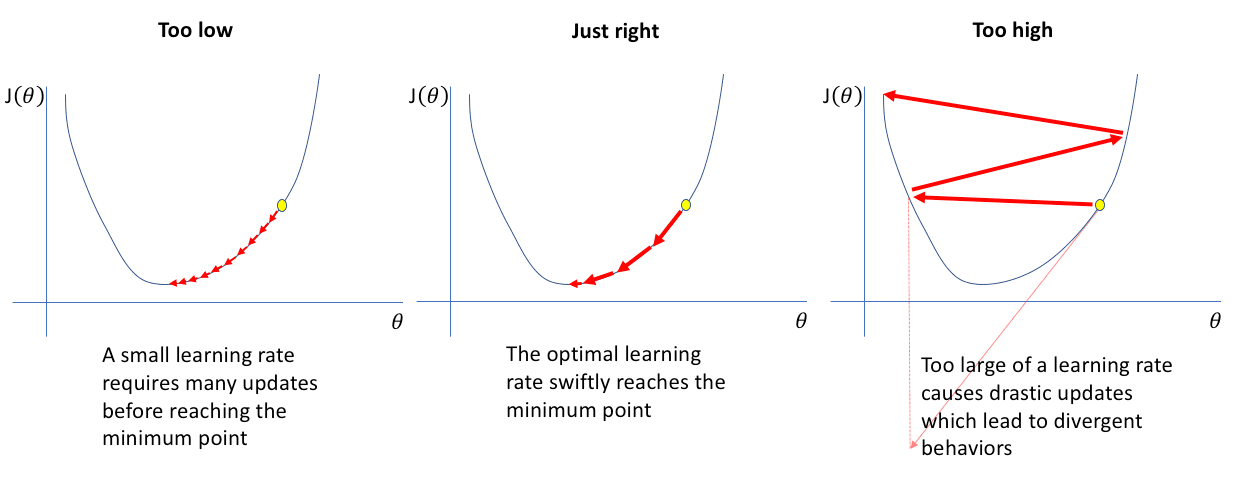
Si la vitesse d'apprentissage est trop faible :

Lorsque la vitesse d'apprentissage est trop faible, le terme dérivée est multiplié par un nombre très petit (par exemple 0,0000001), entraînant des ajustements très minimes de la valeur actuelle de w. Ces petits ajustements sont appelés "petits pas" et, étant donné que la vitesse d'apprentissage est si faible, le deuxième pas est également minuscule. Le résultat de cela est que la coût J diminue, mais à un rythme très lent. La baisse est très lente, mais fonctionnera et prendra beaucoup de temps.

Si la vitesse d'apprentissage est trop élevée :

Lorsque la vitesse d'apprentissage est trop élevée, les mises à jour de w seront très importantes et vous éloigneront du point minimum sur la fonction J. Partant d'un point proche du minimum, si la vitesse d'apprentissage est trop élevée, vous faites un grand pas et vous retrouvez à un point où le coût a en réalité augmenté.

La dérivée à ce nouveau point indique de diminuer w, mais étant donné que la vitesse d'apprentissage est trop grande, vous pouvez faire un grand pas allant d'ici jusqu'ici et surdépasser le minimum à nouveau. Cela peut entraîner un schéma de surpassement et de non-atteinte du minimum. Cela est également connu sous le nom de non-convergence ou même divergence. Nous nous éloignons de plus en plus du minimum, que nous ne pourrons pas atteindre

Une question qui peut se poser est ce qui se passe lorsqu'un des paramètres, w, est déjà à un minimum local de la fonction de coût J. Dans ce cas, une étape de descente de gradient ne changera pas la valeur de w et le coût J restera au minimum local. Considérez ce graphique :

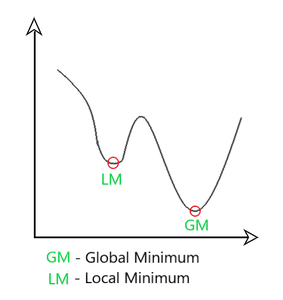
Quand vous arrivez à un minimum local, la pente est égale à 0, donc :

w = w - ∂ * 0 ou W = W.

Si la valeur de w est 5 et ∂ est 0,1, nous pouvons considérer après la première itération :

5 - 0,1 * 0 = 5, donc W est toujours égal à 5.

Si les paramètres ont déjà conduit à un minimum local, des étapes supplémentaires de descente de gradient ne changeront pas les paramètres et maintiendront la solution au minimum local. C'est pourquoi la descente de gradient peut atteindre un minimum local même avec une vitesse d'apprentissage alpha fixe, car des étapes supplémentaires ne changeront pas la solution.

A mesure que nous nous rapprochons d'un minimum local, la descente de gradient prendra automatiquement de plus petits pas. C'est parce que, en nous approchant du minimum local, la dérivée devient plus petite et, par conséquent, les étapes de mise à jour deviennent également plus petites. Cela se produit même si la vitesse d'apprentissage alpha est maintenue à une valeur fixe. C'est l'algorithme de descente de gradient, qui peut être utilisé pour minimiser toute fonction de coût J, et non pas seulement la fonction de coût d'erreur quadratique moyenne utilisée dans la régression linéaire.

Comment appliquer la descente de gradient pour la régression linéaire

Groupons tout ensemble pour nous permettre de former un modèle ! Récapitulons quelques formules :

Modèle de régression linéaire	Fonction de coût	Descente de gradient
𝑓𝑤,𝑏(𝑥(𝑖))=𝑤𝑥(𝑖)+𝑏	1/𝑚* m∑𝑖=0 * (𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))²	𝑤 = 𝑤−𝛼∂/∂𝑤 𝐽(𝑤,𝑏) and 𝑏 = 𝑏−𝛼∂/∂𝑤 𝐽(𝑤,𝑏)

Pour calculer la dérivation pour cela : nous pouvons dire que :

𝑤−𝛼*∂/∂𝑤 *𝐽(𝑤,𝑏) => ∂𝑤 𝐽(𝑤,𝑏) = 1/𝑚 m∑𝑖=0 * (𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))𝑥(𝑖)
𝑏−𝛼*∂/∂𝑤 *𝐽(𝑤,𝑏) => ∂𝑤 𝐽(𝑤,𝑏) = 1/𝑚 m∑𝑖=0 * (𝑓𝑤,𝑏(𝑥(𝑖))−𝑦(𝑖))

Le processus de descente de gradient implique de mettre à jour régulièrement les valeurs de w et b jusqu'à ce que la convergence soit atteinte. Il est important de se rappeler que ceci est un modèle de régression linéaire et f(x) = w * x + b. La dérivée de la fonction de coût par rapport à w est représentée par cette expression et la dérivée de la fonction de coût par rapport à b est représentée par cette expression. Il est important de mettre à jour w et b simultanément à chaque étape.

Une limitation de la descente de gradient est qu'elle peut conduire à un minimum local au lieu d'un minimum global. Un minimum global est le point qui a la valeur la plus basse possible pour la fonction de coût J parmi tous les points possibles. Vous vous rappelez peut-être la surface tracée qui ressemble à un parc extérieur avec des collines, représentant la fonction de coût J, avec le processus de descente de gradient apparaissant comme un chemin de détente à travers les collines.

Rappelez-vous, selon l'endroit où vous initialisez les paramètres (w, b), vous pouvez arriver à des minima locaux différents.

Lorsque l'on utilise la descente de gradient avec une fonction de coût d'erreur carrée dans la régression linéaire, la fonction de coût n'a qu'un seul minimum global. C'est parce que la fonction de coût est une fonction convexe, ce qui signifie qu'elle est en forme de bol et ne peut pas avoir de minima locaux autres que le minimum global. Cette propriété rend la descente de gradient sur une fonction convexe plus prévisible car elle converge toujours vers le minimum global tant que la vitesse d'apprentissage est choisie de manière appropriée.

La descente de gradient vous permettra donc de trouver la meilleure valeur pour former votre modèle et de l'ajuster pour qu'il fonctionne.

La descente de gradient par lots est un type spécifique de descente de gradient qui utilise tous les exemples d'entraînement à chaque étape pour mettre à jour les paramètres du modèle. Le terme "lot" fait référence au fait que l'ensemble des données est utilisé dans chaque itération du processus d'optimisation.

Dans la descente de gradient par lots, les paramètres du modèle sont mis à jour en prenant la moyenne des gradients de la fonction de perte par rapport aux paramètres, calculée sur l'ensemble des données d'entraînement. Cela est en contraste avec d'autres formes de descente de gradient, comme la descente de gradient stochastique, qui mettent à jour les paramètres en utilisant un seul exemple d'entraînement à la fois. "Lot" fait référence au fait que l'ensemble des données est utilisé pour calculer les gradients à chaque mise à jour.

Un graphique de contour de la fonction de coût peut montrer comment la fonction se comporte par rapport aux paramètres. Lorsqu'un axe (par exemple w1) a une plage étroite de valeurs (par exemple entre 0 et 1) et l'autre axe (par exemple w2) a une grande plage de valeurs (par exemple entre 10 et 100), les contours de la fonction de coût peuvent former des ovales ou des ellipses qui sont courtes d'un côté et plus longues de l'autre.

Cela est dû au fait que de petits changements de w1 peuvent avoir un grand impact sur le prix estimé et la fonction de coût (J) car w1 est souvent multiplié par un grand nombre (par exemple la taille de la maison en pieds carrés).

En revanche, il faut un changement beaucoup plus important de w2 pour changer les prévisions et donc de petits changements de w2 ne changent pas la fonction de coût presque autant. Cela peut rendre la descente de gradient peu efficace et prendre beaucoup de temps pour trouver le minimum global.

Mettre à l'échelle les caractéristiques, c'est-à-dire transformer les données d'entraînement de manière à ce que toutes les caractéristiques aient une plage de valeurs similaire, peut aider à rendre les contours de la fonction de coût plus symétriques et à faire converger la descente de gradient plus rapidement.