Introduction

Pour expliquer le fonctionnement des arbres de décision, considérons un exemple d'exécution :

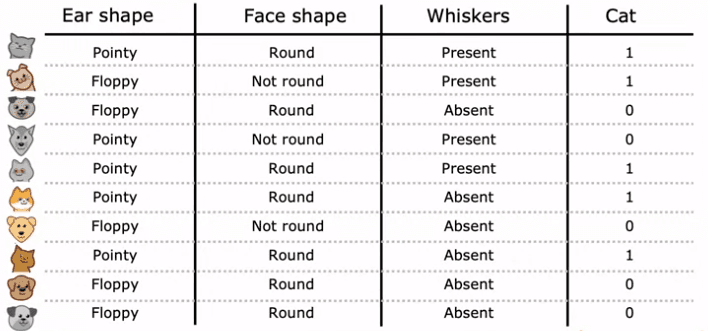
un problème de classification de chats. Imaginez que vous gérez un centre d'adoption de chats et que vous devez classer si un animal est un chat ou non en fonction de ses caractéristiques telles que la forme des oreilles, la forme du visage et la présence de moustaches. Vous avez 10 exemples d'entraînement, 5 d'entre eux étant des chats et 5 étant des chiens. Vos caractéristiques d'entrée, X, sont les valeurs pour la forme des oreilles, la forme du visage et la présence de moustaches, et votre sortie cible, Y, est l'étiquette indiquant si l'animal est un chat ou non.

Dans cet exemple, les caractéristiques X prennent des valeurs catégorielles. Par exemple, la forme des oreilles peut être soit pointue soit molle, la forme du visage peut être soit ronde soit non ronde et la présence de moustaches peut être soit présente soit absente. Il s'agit d'une tâche de classification binaire car les étiquettes sont soit 1 (chat) ou 0 (pas chat).

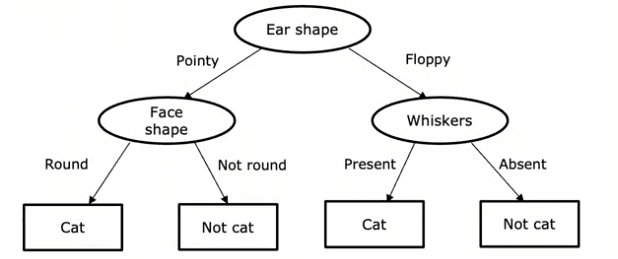
Alors, qu'est-ce qu'un arbre de décision ? C'est un modèle qui est produit par un algorithme d'apprentissage d'arbres de décision et qui ressemble à un arbre, avec des nœuds et des branches. Si vous avez un nouvel exemple de test, vous commencez au nœud racine, regardez la caractéristique écrite à l'intérieur et en fonction de sa valeur, vous allez à gauche ou à droite dans l'arbre jusqu'à ce que vous atteigniez un nœud feuille, qui fait une prédiction.

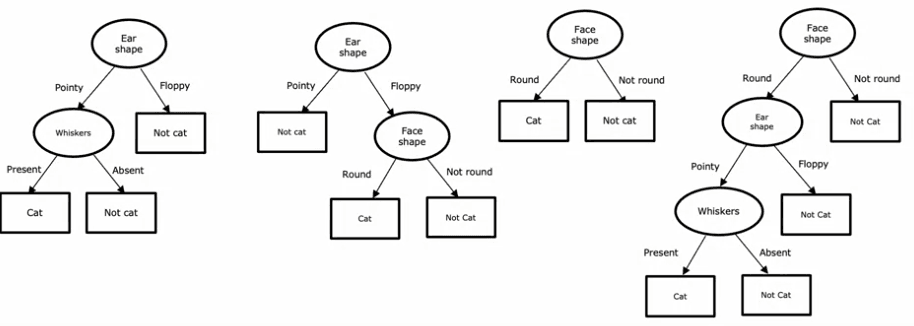
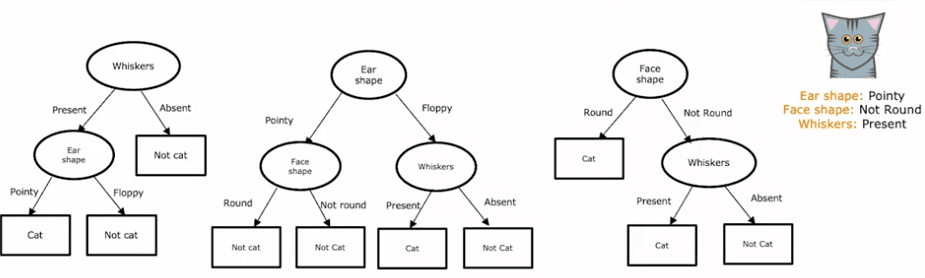
Considérons quelques exemples d'arbres de décision. Dans le premier arbre, si la forme des oreilles de l'exemple de test est pointue, vous examinerez la caractéristique des moustaches pour déterminer si l'animal est un chat ou non. Dans le second arbre, vous examinerez à la fois la forme des oreilles et les moustaches. Les troisième et quatrième arbres sont différents des deux premiers et certains se comporteront mieux que d'autres sur les jeux d'entraînement ou de test.

Les arbres de décision sont un algorithme de machine learning puissant et polyvalent que vous pouvez utiliser dans de nombreuses applications. Ils sont faciles à comprendre et à implémenter et peuvent être combinés avec d'autres algorithmes pour améliorer leur performance. Alors, n'oubliez pas de les ajouter à votre boîte à outils et de commencer à les utiliser dès aujourd'hui !

Processus d'apprentissage

Nous allons passer en revue le processus de construction d'un arbre de décision étape par étape. Nous utiliserons un ensemble d'entraînement de 10 exemples de chats et de chiens pour illustrer le processus.

Étape 1: Choix de la caractéristique pour le nœud racine

La première étape de la construction d'un arbre de décision consiste à décider quelle caractéristique utiliser au nœud racine, le premier nœud en haut de l'arbre de décision. Un algorithme est utilisé pour prendre cette décision, que nous discuterons en détail dans un futur article. Pour l'exemple, disons que nous choisissons la forme de l'oreille en tant que caractéristique au nœud racine.

Étape 2: Division des exemples d'entraînement

Une fois que nous avons décidé de la caractéristique à utiliser au nœud racine, nous divisons les exemples d'entraînement en deux sous-ensembles en fonction de la valeur de la caractéristique de forme d'oreille. Pour cet exemple, nous divisons les 10 exemples d'entraînement en deux groupes de cinq - un groupe pour les oreilles pointues et un groupe pour les oreilles souples.

Étape 3: Choix de la caractéristique pour la branche gauche

Ensuite, nous nous concentrerons sur la branche gauche de l'arbre de décision et déciderons quelle caractéristique utiliser pour diviser les exemples avec des oreilles pointues. Encore une fois, nous utiliserons un algorithme pour prendre cette décision, que nous discuterons à l'avenir. Pour cet exemple, disons que nous choisissons la forme du visage en tant que caractéristique.

Étape 4: Division de la branche gauche

Nous divisons alors les cinq exemples avec des oreilles pointues en deux sous-ensembles en fonction de la forme du visage. Nous finissons avec quatre exemples avec des visages ronds à gauche et un exemple avec un visage non rond à droite. Comme les quatre exemples sur la gauche sont des chats, nous pouvons créer un nœud feuille qui prédit "chat".

Étape 5: Création de la branche droite

Ensuite, nous allons répéter le même processus sur la branche droite de l'arbre de décision, en nous concentrant sur les cinq exemples avec des oreilles molles. Disons que nous choisissons la caractéristique des moustaches pour diviser ces exemples. Après avoir divisé les exemples en fonction de la présence ou de l'absence de moustaches, nous obtenons un exemple à gauche qui est un chat et quatre exemples à droite qui ne sont pas des chats. Nous pouvons créer des nœuds feuille qui prédisent "chat" à gauche et "pas chat" à droite.

Etape 6 : Évaluation des résultats

Tout au long de ce processus, nous avons dû prendre quelques décisions clés. La première était de choisir la caractéristique à utiliser pour diviser les exemples à chaque nœud. Nous avons dû décider de diviser sur la forme de l'oreille, la forme du visage ou les moustaches, en fonction de la caractéristique qui donnerait la plus grande "pureté" des étiquettes. La pureté dans ce contexte signifie avoir des sous-ensembles de données aussi proches que possible soit tous des chats, soit tous des chiens.

Dans la prochaine section, nous discuterons de l'entropie, qui est utilisée pour estimer l'impureté et pour la minimiser. En minimisant l'impureté, nous pouvons atteindre un sous-ensemble très pur d'exemples, ce qui nous permet de faire des prédictions précises.

Construire un arbre de décision est un processus qui implique plusieurs décisions clés. En comprenant les étapes impliquées et les décisions à prendre, vous pouvez acquérir une compréhension plus profonde de la manière dont les arbres de décision fonctionnent et comment ils peuvent être utilisés pour faire des prédictions.

Mesurer la pureté

L'entropie est un concept fondamental en apprentissage automatique qui nous aide à mesurer l'impureté d'un ensemble de données. Cette mesure est particulièrement utile lors de la construction d'arbres de décision.

Imaginons que nous ayons un ensemble de six exemples comprenant trois chats et trois chiens. Nous définissons p_1 comme la fraction d'exemples qui sont des chats (étiquetés en tant que "un").

Dans cet exemple, p_1 est égal à 3/6, ou 0,5. Pour mesurer l'impureté de cet ensemble, nous utilisons la fonction d'entropie, notée H(p_1).

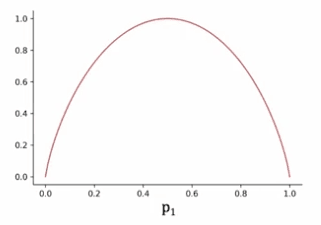
La fonction d'entropie est tracée sur un graphique avec l'axe horizontal représentant p_1 et l'axe vertical représentant la valeur de l'entropie.

Lorsque p_1 est de 0,5, l'entropie est à son plus haut, ce qui est égal à un, ce qui signifie que l'ensemble est le plus impur. Si tous les exemples de l'ensemble sont des chats ou tous les exemples sont des chiens, l'entropie est nulle, ce qui signifie que l'ensemble est pur.

Prenons un autre exemple où nous avons cinq chats et un chien, ce qui nous donne p_1 égal à 5/6 ou 0,83. L'entropie de p_1 est d'environ 0,65. Un autre exemple avec six chats a un p_1 de six sur six, ce qui signifie que l'entropie est nulle. Cela montre que à mesure que la fraction d'exemples positifs (dans ce cas, les chats) augmente, l'impureté diminue et l'ensemble devient pur.

D'un autre côté, un ensemble avec deux chats et quatre chiens a un p_1 de 2/6 ou 1/3, avec une entropie de 0,92. Cet ensemble est plus impur par rapport à l'ensemble avec cinq chats et un chien, car il est plus proche d'un mélange 50-50. Un ensemble de six chiens a un p_1 de zéro et une entropie de zéro, ce qui signifie que l'ensemble est pur.

L'équation réelle de la fonction d'entropie est définie comme négative p_1log_2(p_1) - p_0log_2(p_0), où p_0 est égal à 1 - p_1. La fonction d'entropie commence à zéro, monte à un et redescend à zéro à mesure que la fraction d'exemples positifs dans l'échantillon augmente. La fonction d'entropie est similaire à la perte logistique dans l'apprentissage automatique, mais c'est un sujet pour une autre discussion.

La fonction d'entropie est un outil important pour mesurer l'impureté d'un ensemble de données. Elle est cruciale pour construire des arbres de décision et est définie comme une fonction de la fraction d'exemples positifs dans un échantillon.

Choix d'une séparation

Lors de la construction d'un arbre de décision, le but est de choisir la caractéristique qui divisera les données en sous-ensembles aussi purs que possible. Cela se fait en calculant le gain d'information de chaque caractéristique, qui représente la réduction de l'entropie qui résulte de la division des données en fonction de cette caractéristique.

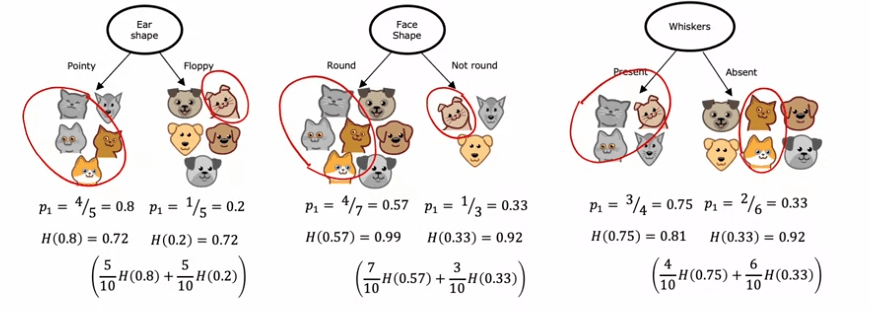
Par exemple, si nous construisons un arbre de décision pour reconnaître les chats et les non-chats, nous pouvons avoir trois caractéristiques à choisir à partir du nœud racine : forme de l'oreille, forme du visage et moustaches. Pour décider quelle caractéristique utiliser, nous calculons le gain d'information de chaque caractéristique, en prenant en compte le nombre d'exemples dans chacun des sous-ensembles résultants.

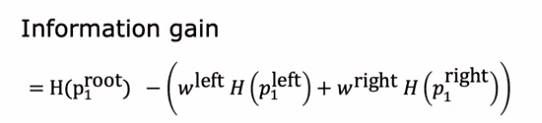
Prenons par exemple la caractéristique de la forme de l'oreille. Si nous divisons sur cette caractéristique, nous aboutirons à deux sous-ensembles, l'un contenant quatre chats sur cinq exemples et l'autre un chat sur cinq exemples. L'entropie de chaque sous-ensemble peut être calculée à l'aide de la formule d'entropie, qui mesure l'impureté des données. Dans ce cas, l'entropie de tous les sous-ensembles s'avère être de 0,72.

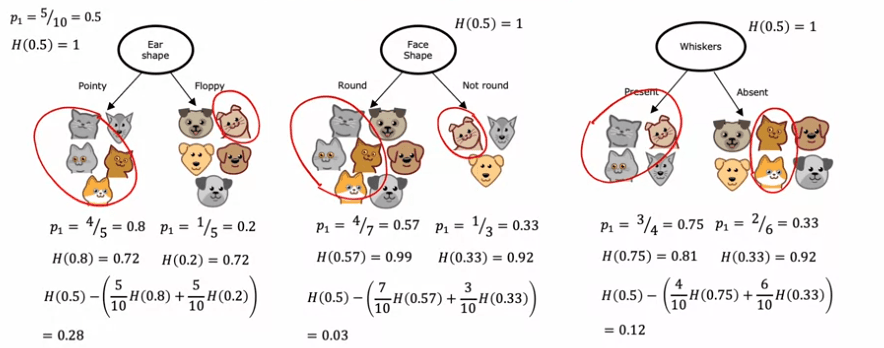
Nous pouvons répéter ce processus pour les deux autres caractéristiques, en calculant l'entropie des sous-ensembles résultants. La caractéristique ayant la moyenne pondérée d'entropie la plus faible sera choisie en tant que caractéristique à séparer au nœud racine.

Notez que dans la construction d'arbres de décision, la réduction de l'entropie est habituellement exprimée comme une réduction par rapport à l'entropie du jeu de données original, plutôt qu'en termes de moyenne pondérée. Mais de toute façon, le but est de choisir la caractéristique qui entraîne une entropie la plus faible, maximisant ainsi la pureté des sous-ensembles résultants.

Combiner la mesure et la séparation

Le processus de construction d'un arbre de décision commence avec tous les exemples d'entraînement à la racine. Ensuite, l'algorithme calcule le gain d'information pour toutes les caractéristiques possibles et la caractéristique avec le plus grand gain d'information est sélectionnée pour la division. Cette division est ensuite utilisée pour créer des branches gauches et droites de l'arbre et les exemples d'entraînement sont envoyés soit à la branche gauche soit à la branche droite en fonction de la valeur de cette caractéristique pour cet exemple.

Le processus de division continue sur les branches gauches et droites de l'arbre jusqu'à ce que le critère d'arrêt soit atteint. Les critères d'arrêt peuvent être différents pour les différentes implémentations de l'algorithme d'arbre de décision, mais les critères d'arrêt courants incluent :

• Lorsqu'un nœud est à 100 % d'une seule classe
• Lorsque l'entropie des données au nœud est nulle
• Lorsque la profondeur maximale de l'arbre a été atteinte
• Lorsque le gain d'information provenant de divisions supplémentaires est inférieur à un seuil
• Lorsque le nombre d'exemples dans un nœud est inférieur à un seuil

Le processus de construction d'un arbre de décision peut également être considéré comme un algorithme récursif, car la manière dont vous construisez un arbre de décision à la racine est en construisant d'autres arbres de décision plus petits dans les sous-branches gauches et droites. La manière dont l'algorithme construit ces sous-arbres de décision est en répétant le processus de calcul du gain d'information pour toutes les caractéristiques possibles et en divisant les données en conséquence, jusqu'à ce que les critères d'arrêt soient atteints.

One-hot encoding

Dans cette section, nous explorerons comment gérer les caractéristiques qui peuvent prendre plus de deux valeurs en apprentissage automatique. Nos exemples précédents avaient des caractéristiques telles que la forme de l'oreille, la forme du visage et les moustaches qui ne pouvaient prendre que deux valeurs possibles, soit pointues ou molles, rondes ou non rondes et présentes ou absentes, respectivement.

Cependant, que se passe-t-il si une caractéristique telle que la forme de l'oreille peut prendre trois valeurs possibles : pointues, molles ou ovales ? Pour aborder ce problème, nous utiliserons une technique appelée codage one-hot.

Le codage one-hot consiste à remplacer une caractéristique catégorique par k caractéristiques binaires, où k est le nombre de valeurs possibles pour la caractéristique d'origine. Dans ce cas, k est 3 pour la caractéristique forme d'oreille. Au lieu d'avoir une caractéristique pour la forme de l'oreille, nous créerons trois nouvelles caractéristiques, une pour les oreilles pointues, une pour les oreilles molles et une pour les oreilles ovales. Chacune de ces caractéristiques ne peut prendre que deux valeurs possibles, 0 ou 1, et une seule d'entre elles aura une valeur de 1, d'où le nom de codage one-hot.

Avec cette approche, nous sommes de retour à la configuration originale où chaque caractéristique ne peut prendre que deux valeurs. L'algorithme d'apprentissage d'arbre de décision peut être appliqué à ces données sans aucune modification. La technique de codage one-hot peut également être appliquée à d'autres types de modèles d'apprentissage automatique, tels que les réseaux de neurones.

Le codage one-hot est une technique qui permet aux arbres de décision et à d'autres modèles d'apprentissage automatique de travailler avec des caractéristiques qui peuvent prendre plus de deux valeurs. En convertissant les caractéristiques catégoriques en un ensemble de caractéristiques binaires, l'algorithme d'apprentissage automatique peut être alimenté en entrées qui sont des nombres au lieu de valeurs catégoriques.

Continous valued features

Nous allons explorer comment modifier l'algorithme d'arbre de décision pour travailler avec des caractéristiques qui ne sont pas seulement des valeurs binaires, mais des valeurs continues, c'est-à-dire des caractéristiques qui peuvent prendre n'importe quel nombre. Pour illustrer cela, utilisons une version modifiée du jeu de données du centre d'adoption de chats qui comprend une nouvelle caractéristique : le poids de l'animal en livres. Cette caractéristique est utile pour déterminer si un animal est un chat ou non.

Pour intégrer cette caractéristique dans l'algorithme d'apprentissage d'arbre de décision, nous devons considérer la division sur la caractéristique de poids ainsi que les autres caractéristiques telles que la forme de l'oreille, la forme du visage et les moustaches. Pour déterminer comment diviser sur la caractéristique de poids, nous devons considérer de nombreuses valeurs seuil différentes et choisir celle qui donne le plus grand gain d'information.

Par exemple, si nous considérons la division des données en fonction du poids étant inférieur ou égal à 8, nous allons diviser les données en deux sous-ensembles. Nous calculons ensuite le gain d'information en calculant l'entropie à la racine et en soustrayant l'entropie des deux sous-ensembles. Cependant, nous devrions essayer d'autres valeurs également et choisir celle qui donne le plus grand gain d'information.

En général, nous classons les exemples selon la valeur de la caractéristique et choisissons les milieux entre la liste triée d'exemples comme les valeurs seuil possibles à considérer. Pour chaque valeur seuil, nous calculons le gain d'information et choisissons le seuil qui donne le plus grand gain d'information. Si le gain d'information provenant de la division sur la valeur continue de la caractéristique est meilleur que celui provenant de la division sur toute autre caractéristique, alors nous choisissons de diviser à cette caractéristique.

Pour résumer, pour faire fonctionner l'arbre de décision avec des caractéristiques à valeur continue, nous essayons différentes valeurs seuil, effectuons le calcul habituel de gain d'information et divisons sur la caractéristique à valeur continue si elle donne le plus grand gain d'information possible. De cette façon, l'arbre de décision peut gérer les caractéristiques à valeur continue et faire des prévisions en fonction d'elles.

Implémenter un arbre de décision

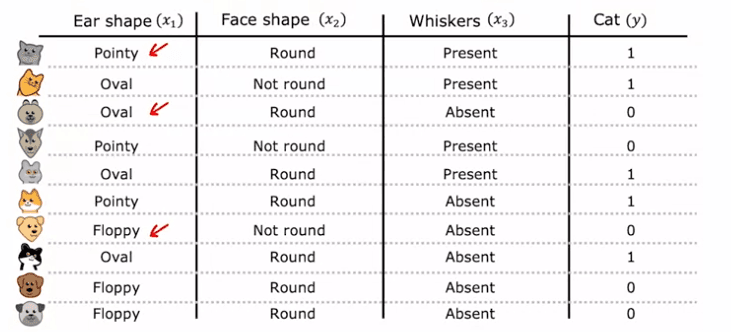
Nous allons utiliser le codage one-hot pour encoder les caractéristiques catégoriques. Elles seront les suivantes :

Forme de l'oreille : Pointue = 1, Molle = 0 Forme du visage : Ronde = 1, Pas ronde = 0 Moustaches : Présentes = 1, Absentes = 0 Par conséquent, nous avons deux ensembles : X_train : pour chaque exemple, ils contiennent 3 caractéristiques :

• Forme du visage (1 si ronde, 0 sinon)
• Forme de l'oreille (1 si pointue, 0 sinon)
• Moustaches (1 si présentes, 0 sinon)

y_train : si l'animal est un chat

• 1 si l'animal est un chat
• 0 sinon

 import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from utils import *

X_train = np.array([[1, 1, 1],
[0, 0, 1],
 [0, 1, 0],
 [1, 0, 1],
 [1, 1, 1],
 [1, 1, 0],
 [0, 0, 0],
 [1, 1, 0],
 [0, 1, 0],
 [0, 1, 0]])

y_train = np.array([1, 1, 0, 0, 1, 1, 0, 1, 0, 0])

#For instance, the first example
X_train[0]

Le résultat devrait être :

 tableau([1, 1, 1])

La première instance a une forme d'oreille pointue, une forme de visage circulaire et est équipée de moustaches.

Concernant les nœuds, nous calculons le gain d'information pour chaque caractéristique, puis divisons le nœud sur la base de la caractéristique ayant le plus grand gain d'information. Cela est réalisé en évaluant l'entropie du nœud par rapport à l'entropie pondérée des deux nœuds de division résultants.

Il est important de noter que le nœud racine englobe tous les animaux de notre jeu de données, avec 𝑝𝑛𝑜𝑑𝑒1 représentant la proportion de classe positive (chats) dans le nœud racine.

𝑝𝑛𝑜𝑑𝑒1=5/10=0,5

Ceci est la formule à mettre en place :

𝐻(𝑃𝑛𝑜𝑑𝑒1) = −𝑃𝑛𝑜𝑑𝑒1 log2(𝑃𝑛𝑜𝑑𝑒1) − (1 − 𝑃𝑛𝑜𝑑𝑒1) log2(1 − 𝑃𝑛𝑜𝑑𝑒1)

 def entropy(p):
    if p == 0 or p == 1:
        return 0
    else:
        return -p * np.log2(p) - (1- p)*np.log2(1 - p)
    
print(entropy(0.5))

Pour clarifier, calculons le gain d'information en scindant le nœud pour chacune des caractéristiques. Pour ce faire, nous allons écrire certaines fonctions.

 def split_indices(X, index_feature):
    """Donné un jeu de données et une caractéristique d'index, retournez deux listes pour les deux nœuds scindés, le nœud gauche comporte les animaux qui ont
    cette caractéristique = 1 et le nœud droit ceux qui ont la caractéristique = 0
    index feature = 0 => forme d'oreille
    index feature = 1 => forme de visage
    index feature = 2 => moustaches
    """
    left_indices = []
    right_indices = []
    for i,x in enumerate(X):
        if x[index_feature] == 1:
            left_indices.append(i)
        else:
            right_indices.append(i)
    return left_indices, right_indices
    
split_indices(X_train, 0)

Le résultat devrait être :

([0, 3, 4, 5, 7], [1, 2, 6, 8, 9])

Maintenant, nous devons créer une autre fonction pour calculer l'entropie pondérée dans les nœuds divisés. Comme discuté précédemment, nous devons déterminer :

• 𝑤gauche et 𝑤droit, la proportion d'animaux dans chaque nœud.
• 𝑝gauche et 𝑝droit, la proportion de chats dans chaque division.

Il est crucial de faire la distinction entre ces deux définitions. Pour donner un exemple, si nous divisons le nœud racine sur la base de la caractéristique d'index 0 (Forme de l'oreille), le nœud gauche contiendra les animaux 0, 3, 4, 5 et 7. Les valeurs suivantes s'appliqueraient alors :

• 𝑤gauche = 5/10 = 0,5
• 𝑝gauche = 4/5 = 0,8
• 𝑤droit = 5/10 = 0,5
• 𝑝droit = 1/5 = 0,2

 def weighted_entropy(X,y,left_indices,right_indices):
    """
    This function takes the splitted dataset, the indices we chose to split and returns the weighted entropy.
    """
    w_left = len(left_indices)/len(X)
    w_right = len(right_indices)/len(X)
    p_left = sum(y[left_indices])/len(left_indices)
    p_right = sum(y[right_indices])/len(right_indices)
    
    weighted_entropy = w_left * entropy(p_left) + w_right * entropy(p_right)
    return weighted_entropy
    
left_indices, right_indices = split_indices(X_train, 0)
weighted_entropy(X_train, y_train, left_indices, right_indices)

Result : 

0.7219280948873623

Ainsi, l'entropie pondérée dans les deux nœuds divisés est de 0,72. Pour calculer le gain d'information, nous soustractons cette valeur de l'entropie dans le nœud que nous avons sélectionné pour diviser (dans ce cas, le nœud racine).

 def information_Gain(X, y, left_indices, right_indices):
    """
    Ici, X a les éléments dans le nœud et y est leurs classes respectives
    """
    p_node = sum(y)/len(y)
    h_node = entropy(p_node)
    w_entropy = weighted_entropy(X,y,left_indices,right_indices)
    return h_node - w_entropy
    
information_Gain(X_train, y_train, left_indices, right_indices)

Resultat: 0.2780719051126377

Maintenant, calculons le gain d'information si nous divisons le nœud racine pour chaque caractéristique :

 for i, feature_name in enumerate(['Ear Shape', 'Face Shape', 'Whiskers']):
    left_indices, right_indices = split_indices(X_train, i)
    i_gain = information_gain(X_train, y_train, left_indices, right_indices)
    print(f"Feature: {feature_name}, information gain if we split the root node using this feature: {i_gain:.2f}")
    
Result:

Feature: Ear Shape, information gain if we split the root node using this feature: 0.28
Feature: Face Shape, information gain if we split the root node using this feature: 0.03
Feature: Whiskers, information gain if we split the root node using this feature: 0.12

Ainsi, la meilleure caractéristique pour effectuer la division est la forme de l'oreille. Le code ci-dessous montre l'action de la division. Il n'est pas nécessaire de comprendre en profondeur ce bloc de code.

 tree = []
build_tree_recursive(X_train, y_train, [0,1,2,3,4,5,6,7,8,9], "Root", max_depth=1, current_depth=0, tree = tree)
generate_tree_viz([0,1,2,3,4,5,6,7,8,9], y_train, tree)

Result:

 Depth 0, Root: Split on feature: 0
 - Left leaf node with indices [0, 3, 4, 5, 7]
 - Right leaf node with indices [1, 2, 6, 8, 9]

Le processus est itératif, ce qui signifie que nous répétons ces calculs pour chaque nœud jusqu'à ce qu'une condition d'arrêt soit remplie, telle que:

• Si la profondeur de l'arbre après la division dépasse une limite spécifiée
• Si le nœud résultant ne contient que des instances d'une seule classe
• Si le gain d'information à partir de la division est inférieur à un certain seuil.

L'arbre final ressemblerait au diagramme montré.

 tree = []
build_tree_recursive(X_train, y_train, [0,1,2,3,4,5,6,7,8,9], "Root", max_depth=2, current_depth=0, tree = tree)
generate_tree_viz([0,1,2,3,4,5,6,7,8,9], y_train, tree)

Result: 

 Depth 0, Root: Split on feature: 0
- Depth 1, Left: Split on feature: 1
  -- Left leaf node with indices [0, 4, 5, 7]
  -- Right leaf node with indices [3]
- Depth 1, Right: Split on feature: 2
  -- Left leaf node with indices [1]
  -- Right leaf node with indices [2, 6, 8, 9]

Les arbres d'ensembles

L'un des inconvénients de l'utilisation d'un seul arbre de décision est sa vulnérabilité aux petits changements dans les données. Pour surmonter ce défaut et rendre le modèle plus robuste, un ensemble d'arbres peut être utilisé. Un ensemble d'arbres signifie la création de plusieurs arbres de décision au lieu d'un seul.

Par exemple, si un seul arbre de décision est utilisé pour classer les chats et les non-chats, de petits changements dans les données peuvent entraîner la génération d'un arbre complètement différent. Cette absence de robustesse est la raison pour laquelle les ensembles d'arbres sont souvent plus précis que les arbres de décision uniques.

Pour classer un nouvel exemple de test, l'ensemble d'arbres est utilisé en exécutant l'exemple de test à travers chaque arbre et en prenant un vote majoritaire sur les prédictions faites par chaque arbre. La prédiction finale est celle qui reçoit la majorité des votes. Cette approche rend l'algorithme dans son ensemble moins sensible aux prédictions faites par un seul arbre et, par conséquent, plus robuste.

Nous allons explorer la technique d'échantillonnage avec remplacement, qui est une méthode clé utilisée pour construire l'ensemble d'arbres.

Sampling

L'échantillonnage avec remplacement est une technique utilisée pour construire un ensemble d'arbres en apprentissage automatique. Il consiste à créer plusieurs ensembles d'entraînement légèrement différents à partir de l'ensemble d'entraînement original. Cela se fait en sélectionnant au hasard des exemples de l'ensemble original et en les ajoutant à un nouvel ensemble, puis en remettant l'exemple sélectionné dans l'ensemble original et en répétant le processus jusqu'à ce que le nouvel ensemble ait le nombre d'exemples souhaité. Certains exemples de l'ensemble original peuvent être répétés dans le nouvel ensemble et certains peuvent ne pas être inclus du tout. Ce processus permet de créer de nouveaux ensembles d'entraînement similaires mais différents de l'ensemble original, ce qui est important pour construire un ensemble d'arbres.

L'algorithme Random forest

Dans cet section, nous allons discuter de l'algorithme Random Forest, un puissant algorithme d'ensemble d'arbres qui surpasse un seul arbre de décision. L'algorithme Random Forest est créé en construisant plusieurs arbres de décision sur différents ensembles d'entraînement générés à l'aide d'une technique appelée "échantillonnage avec remplacement". Pour un ensemble d'entraînement de taille M, l'algorithme génère B nouveaux ensembles d'entraînement en sélectionnant aléatoirement M exemples de l'ensemble original, avec remplacement. Chaque nouvel ensemble d'entraînement est utilisé pour former un arbre de décision, ce qui conduit à un total de B arbres de décision. La prédiction finale est effectuée en faisant voter chaque arbre sur la réponse correcte. Le nombre d'arbres, B, est généralement d'environ 100, mais des valeurs allant de 64 à 228 sont également courantes. Le fait de définir B à une valeur plus élevée n'affecte pas significativement les performances au-delà d'un certain point.

Pour améliorer encore les performances de l'algorithme, une modification est effectuée pour randomiser le choix de la fonctionnalité à chaque nœud. Au lieu de sélectionner la fonctionnalité avec le plus grand gain d'information parmi toutes les fonctionnalités disponibles, un sous-ensemble aléatoire de K (moins que N) fonctionnalités est choisi et la fonctionnalité avec le plus grand gain d'information de ce sous-ensemble est sélectionnée. Cette modification aboutit à la création de l'algorithme Random Forest, qui est plus robuste et précis qu'un seul arbre de décision.

L'algorithme Random Forest explore des petits changements à l'ensemble d'entraînement à travers la procédure d'échantillonnage avec remplacement, en moyennant sur tous ces changements. Cela rend moins probable qu'un changement apporté à l'ensemble d'entraînement ait un impact significatif sur la sortie globale de l'algorithme.

En conclusion, l'algorithme Random Forest est une technique d'apprentissage automatique efficace et robuste. Bien qu'il soit dépassé par un autre algorithme appelé Boosted Decision Trees, c'est encore un outil utile pour les ingénieurs en apprentissage automatique.

XGBoost

XGBoost Dans cette section, nous allons discuter de XGBoost, la mise en œuvre la plus couramment utilisée d'ensembles d'arbres de décision. XGBoost est une implémentation rapide et efficace en open source des arbres boostés, qui est une modification de l'algorithme d'arbre de décision. Le boost se concentre sur les exemples que les arbres de décision précédents de l'ensemble ont mal classés, permettant à l'algorithme d'apprendre plus rapidement.

Pour implémenter le boost, l'algorithme examine les arbres de décision formés jusqu'à présent et détermine les exemples qui sont encore mal classés. À chaque itération, une plus grande probabilité est donnée à la sélection d'exemples sur lesquels l'ensemble ne se comporte toujours pas bien, en concentrant l'attention de l'arbre de décision suivant de l'ensemble. Les détails mathématiques sur la façon d'augmenter la probabilité sont complexes, mais l'implémentation open source de XGBoost s'en occupe.

XGBoost a également une régularisation intégrée pour éviter le surapprentissage, ce qui en fait un algorithme très compétitif dans les compétitions d'apprentissage automatique. Au lieu d'utiliser un échantillonnage avec remplacement, XGBoost attribue des poids différents à différents exemples d'apprentissage, ce qui le rend encore plus efficace. Pour utiliser XGBoost, il suffit d'importer la bibliothèque et d'initialiser un modèle en tant que classificateur ou régressif XGBoost.

En conclusion, XGBoost est un algorithme puissant et largement utilisé pour les ensembles d'arbres de décision. Son implémentation open source est efficace et facile à utiliser, et il a été couronné de succès dans de nombreuses compétitions d'apprentissage automatique et applications commerciales.

Quand utiliser un arbre de décision ?

En choisissant entre les arbres de décision et les réseaux de neurones en tant qu'algorithmes d'apprentissage automatique, il est important de prendre en compte le type de données avec lesquelles vous travaillez et les exigences spécifiques de votre tâche.

Les arbres de décision et les ensembles d'arbres sont un type d'algorithme d'apprentissage supervisé qui conviennent bien aux données tabulaires ou structurées, telles que les données stockées au format de tableur. Ils utilisent une structure en arbre pour effectuer des prévisions en fonction des valeurs des caractéristiques des données. Les arbres de décision sont rapides à entraîner et peuvent être interprétables, ce qui signifie que vous pouvez comprendre comment le modèle prend des décisions, surtout pour les petits arbres avec seulement quelques dizaines de nœuds.

Cependant, les arbres de décision ne sont pas aussi efficaces lorsqu'ils travaillent avec des données non structurées, telles que des images, des vidéos, des sons ou du texte. D'un autre côté, les réseaux de neurones sont un type de réseau neuronal artificiel qui peuvent gérer tous les types de données, y compris les données structurées, non structurées et mixtes. Les réseaux de neurones sont généralement plus puissants et peuvent atteindre de meilleures performances sur des tâches complexes, mais ils peuvent être plus lents à entraîner, surtout pour les réseaux importants. De plus, les réseaux de neurones peuvent bénéficier du transfert d'apprentissage, où un pré-entraînement sur un ensemble de données plus important peut améliorer les performances du modèle sur une tâche plus petite et liée.

En conclusion, le choix entre les arbres de décision et les réseaux de neurones dépendra du type de données avec lesquelles vous travaillez et des exigences spécifiques de votre tâche. Bien que les arbres de décision soient rapides à entraîner et interprétables, ils ne sont pas aussi efficaces sur les données non structurées. Les réseaux de neurones sont plus puissants et peuvent gérer tous les types de données, mais ils peuvent être plus lents à entraîner. Les deux algorithmes ont leurs forces et leurs faiblesses, et le choix adéquat dépendra de la tâche spécifique en question.