Les Neurones

Comment peut-on recréer nos neurones par une machine ? D'abord, nous devons comprendre ce qu'est un neurone ?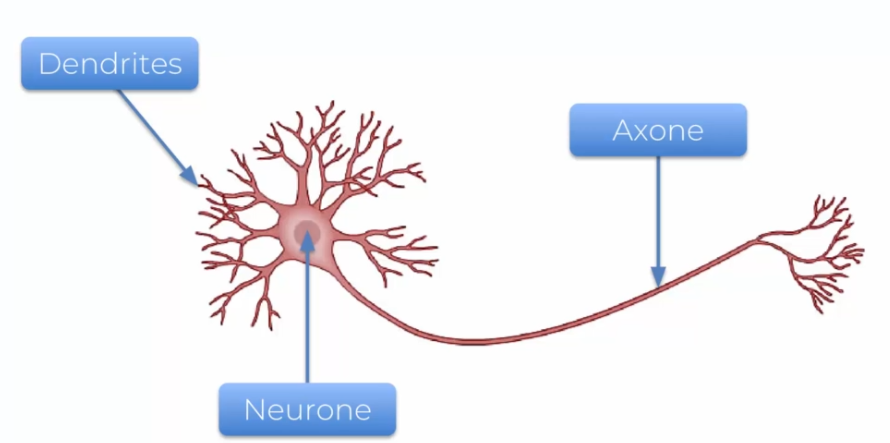

• Les Dendrites: elles servent à un neurone à recevoir les informations
• Les Axones: elles servent à envoyer les informations aux autres neurones

Vous l'aurez compris, les neurones ont besoin d'être plusieurs pour fonctionner correctement. Ainsi les Dentrites et Axones permettent au cerveau humain d'interagir. Mais alors comment peut-on le représenter ?

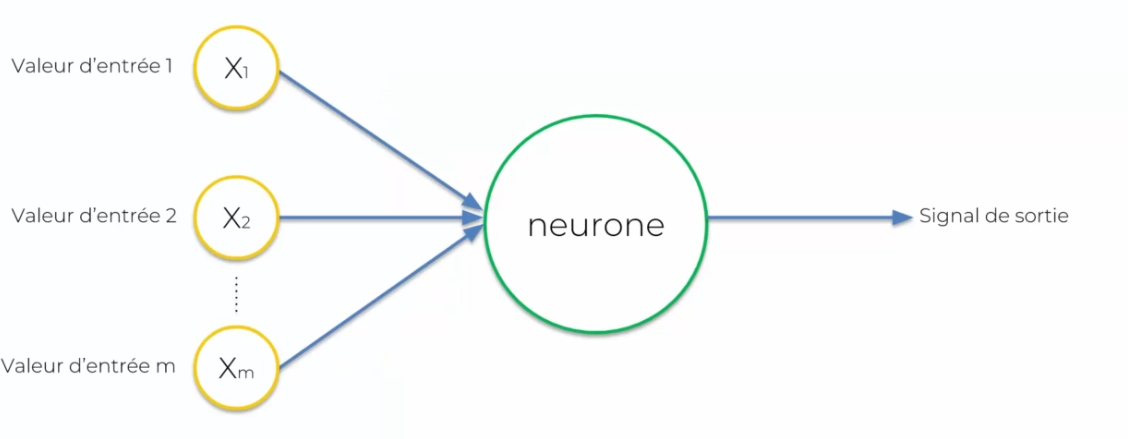
On ne parle plus de dendrites ou axones, mais de valeur d'entrée et de signal de sortie.

• Les entrées seront représentées en jaune
• Le neurone sera représenté en vert

Chacune des entrées sera représentée par un neurone ou des données que l'on donnera en entrée. Le neurone fera les traitements de ces données pour en ressortir des décisions : la valeur de sortie (ou signal). Il est important de standardiser nos valeurs d'entrées : on retire la moyenne divisée par l'écart type ou en mettant les variables sur une variable de 0 à 1, nous reviendrons plus tard sur cette standardisation. Nous devons aussi parler de la connexion entre les valeurs d'entrée et le neurone : le poids. Ce poids doit être continuellement ajusté de sorte que chaque donnée en entrée, pour que le neurone lors de ces calcules puisse prendre en compte les données en sortie.

La fonction d'activation

La fonction d'activation est dans le neurone pour créer une valeur de sortie du neurone. Il en existe plusieurs :

La fonction Seuil

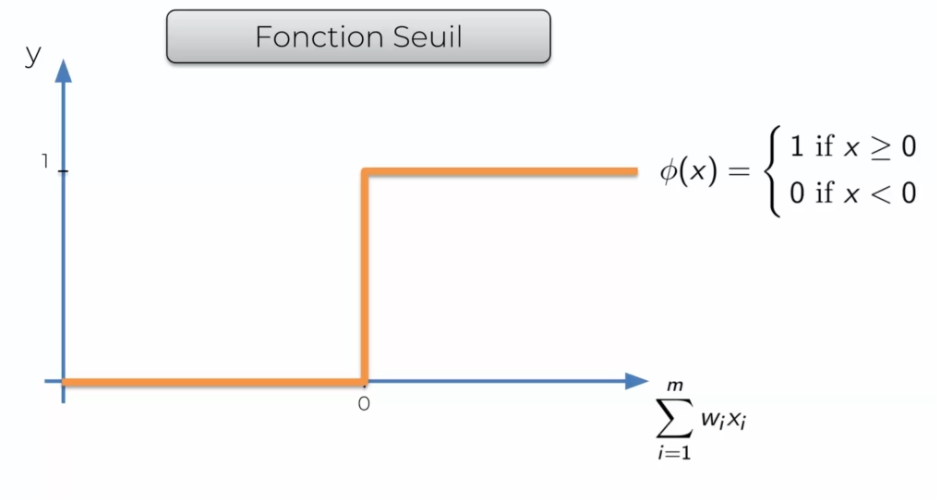
Elle est très simple, en gros elle va renvoyer 0 si le signal d'entrée est négatif et 1 s'il est possible ou null.

La fonction Sigmoïde

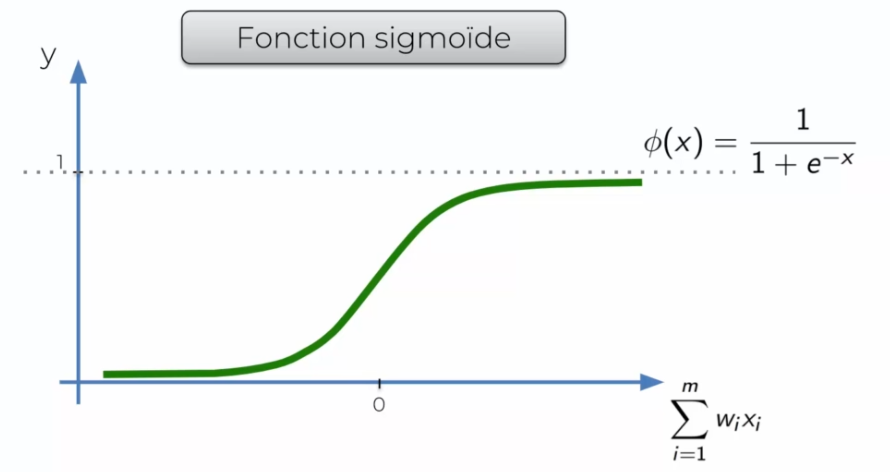
Elle est très ressemblante à la fonction de Seuil, mais est plus lisse. On arrive lentement à 1 et non plus directement. On l'utilise souvent dans la dernière couche, car elle ressort une probabilité.

La fonction Redresseur

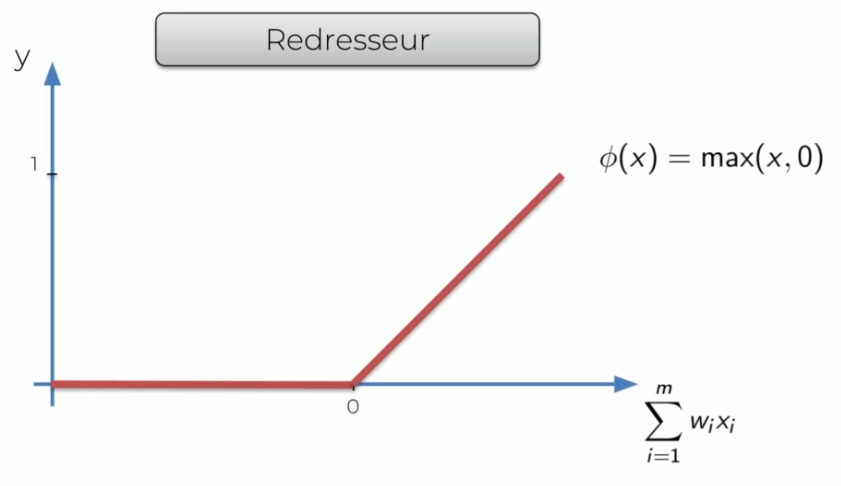
C'est l'une des fonctions les plus populaires, si X est inférieur à 0 elle va couper le signal sinon elle va juste renvoyer le signal.

La tangente hyperbolique (tanh)

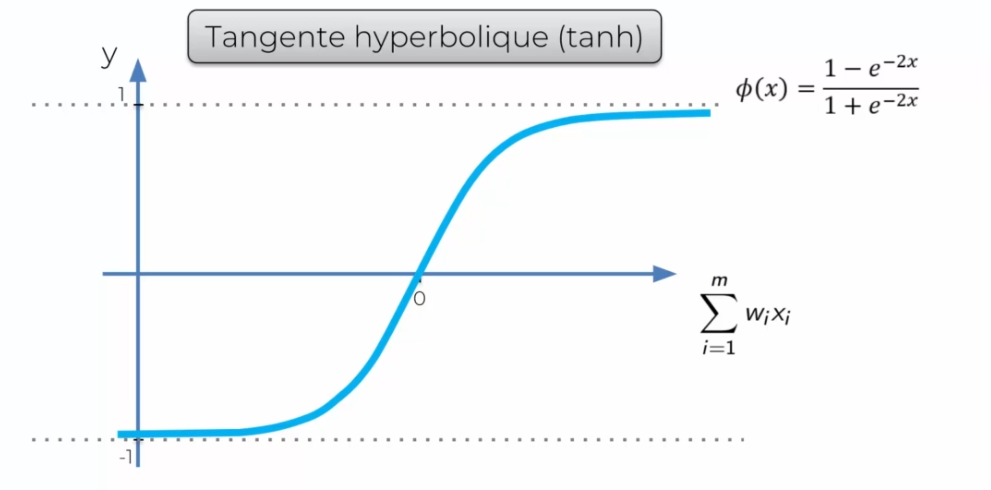
On l'utilise souvent quand on n’a pas une probabilité à ressortir.

La fonction d'activation la plus adaptée ?

Dans le cas suivant :

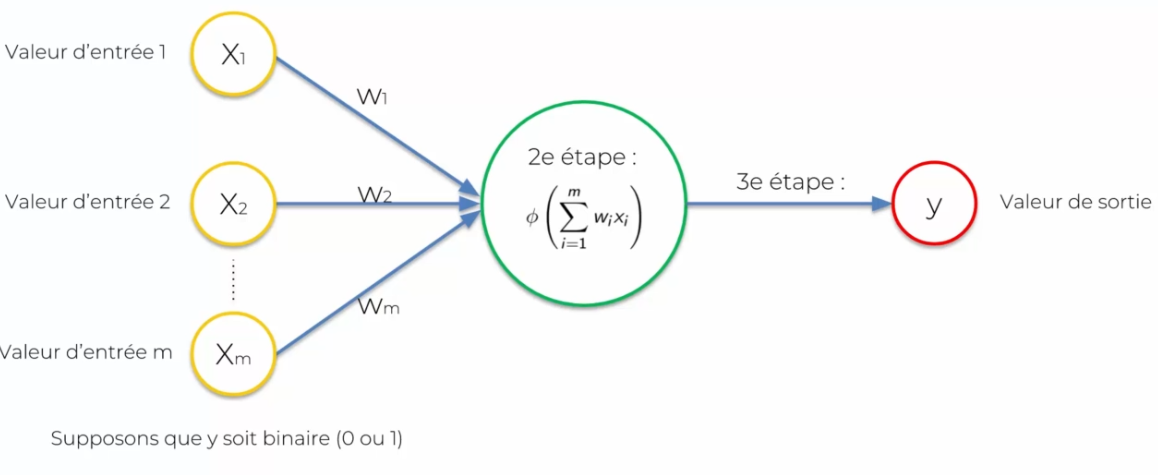
Nous supposons que la réponse soit binaire (0 ou 1) :

• Fonction d'activation de seuil : elle retournera soit 0 ou 1
• Fonction d'activation sigmoide : elle ressort une sorte de probabilité et l'on peut donc ensuite décider d'une règle

Passons sur un cas plus compliqué :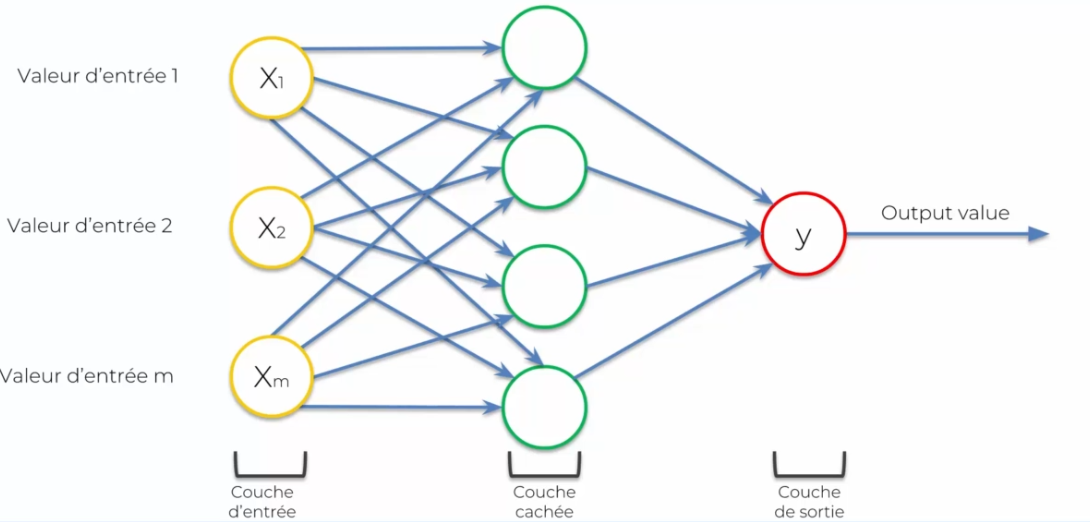

On voit que l'on plus de neurones, de manière généralement on utilisera :

• La fonction redresseur: elle permettra selon X, s'il est élevé on laisse passer, sinon on bloque Pour ensuite sur Y on appliquera :
• La fonction sigmoide: qui permettra d'appliquer une probabilité

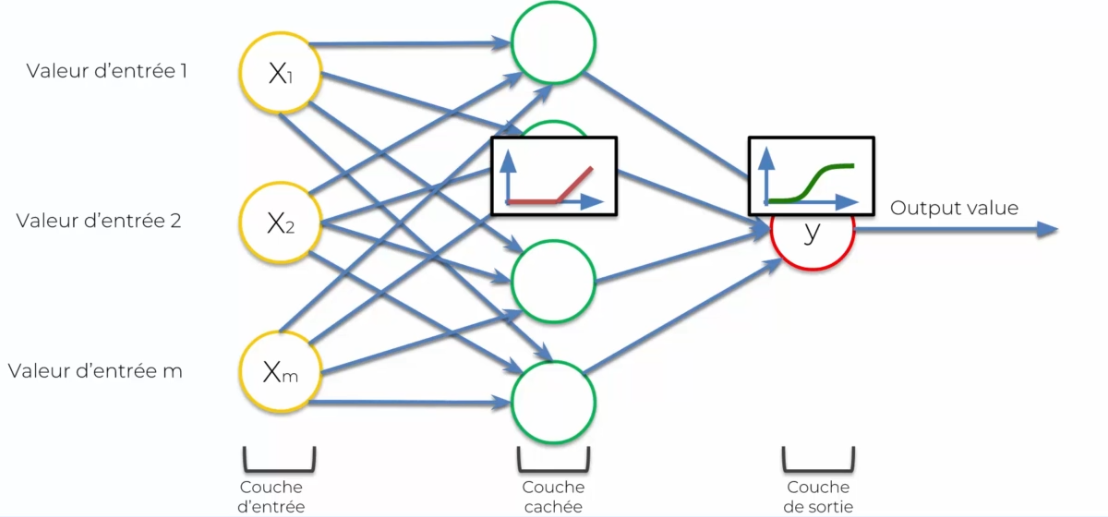
Le fonctionnement d'un réseau

Imaginons que l'on veut vendre une maison, on se pose dans un premier temps :

• Quel sera le prix de vente de cette maison ?

On suppose que notre réseau de neurones est entrainé (les poids sur les synapses sont définis). On aura plusieurs variables d'entrées :

• Surface (m2)
• Nombre de chambres (X2)
• Distance du centre (km)
• Âge

On a besoin d'ajouter des couches cachées : toutes les synapses sont connectées à un neurone, et parfois elles auront un poids différent de 0. Mais comment cela est possible que certains poids soient à 0 ? Car on va différencier les entrées et affecter à chaque neurone une spécialisation. Ainsi pour un neurone X, seules certaines synapses sont pertinentes, alors que les autres non. C'est là qu'entre en jeu la couche cachée qui permet de spécialiser les données en entrées, en fonction d'un domaine précis, et rejetées (valeur à 0) dont elle n'a plus besoin.

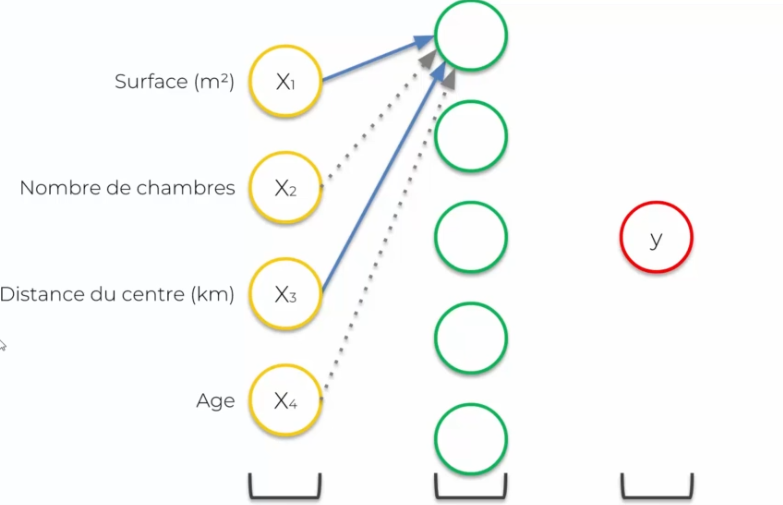
Les combinaisons deviennent donc importantes pour un domaine précis, car il permettra à un neurone précis d'être spécialisé dans un domaine X et donc de ressortir des données plus précises. Ainsi le réseau de neurones prendra des décisions en fonction des données en entrée.

Ainsi notre couche cachée passera les données directement à Y (couche de sortie) qui permettra de faire ressortir un prix de vente.

L"entrainement d'un réseau

Si l'on reprend le réseau de neurone précédent :

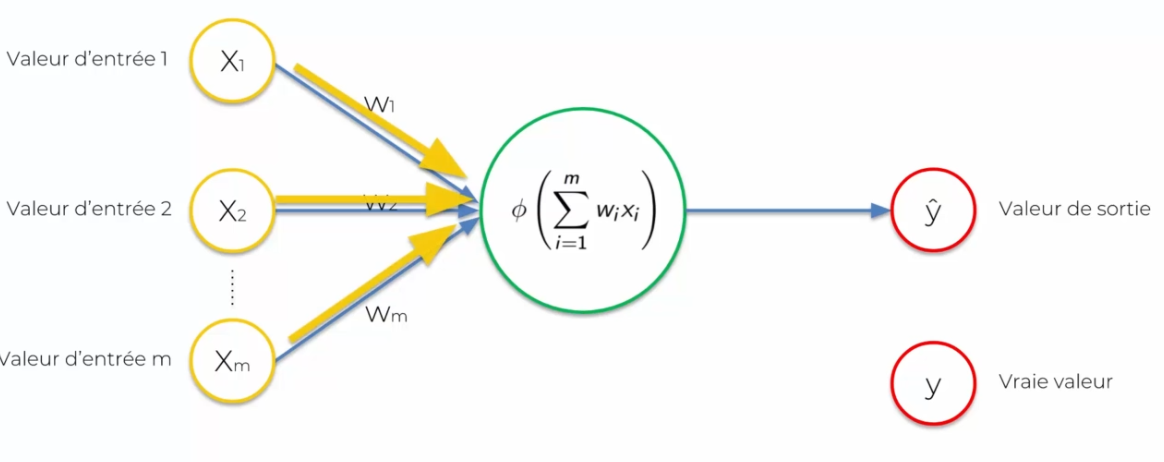
On remarque que l'on a changé y en sortie par ^y, cela vient du fait que cette valeur sera perçue comme une prédiction, alors qu'Y sera la vraie valeur.

• Vraie valeur signifie que c'est une valeur attendue lors de l'entrainement
• Prédiction signifie que c'est le résultat obtenu par notre réseau de neurones

Pour alors savoir si notre valeur est bonne ou non, on va la comparer avec la vraie valeur. On applique alors une fonction de cout :

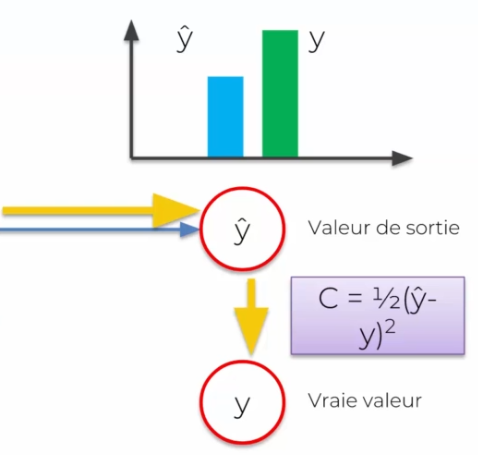
Notre objectif est de minimiser la fonction de cout au maximum. Pour cela, après chaque cout, il est important de mettre à jour les fonctions de poids de chaque synapse. Alors pourquoi sur les synapses ? Car ils sont les seuls que l'on peut mettre à jour. Chaque fonction d'activations n'aura pas un impact direct.

Cet ajustement permettra de savoir le cout de chaque synapse, l'adapter et donc réduire la fonction de cout finale pour réduire l'écart en ^Y et Y. Une fois que le réseau est proche de la vraie valeur, on considère l'entrainement terminé et le réseau apte à commencer.

Attention: il est rare que le cout soit égal à 0 !

Mais comment cela se passe avec plusieurs lignes ?

Le fait d'entrainer un réseau de neurones sur plusieurs lignes, plusieurs données, s'appelle une époque. Comment cela fonctionne :

• On passe chaque ligne dans le même réseau de neurones
• Au fur et à mesure des passages de lignes, on obtient plusieurs ^Y pour chaque ligne
• On calcule alors la valeur de cout pour tous les ^Y.
• On fait ensuite la somme de tous les couts pour chaque individu
• On propage cette information dans le réseau de neurones et l'on met à jour le poids par individu

On appelle ce processus global de gauche à droite et l'on met à jour les poids : la retropropagation.

L'algorithme du gradient

Précedement nous avons parlé des fonctions de couts, dans notre exemple nous avons utilisé une simple fonction de couts. La technique de brut force dit, que pour un poid la meilleur valeur est définie:

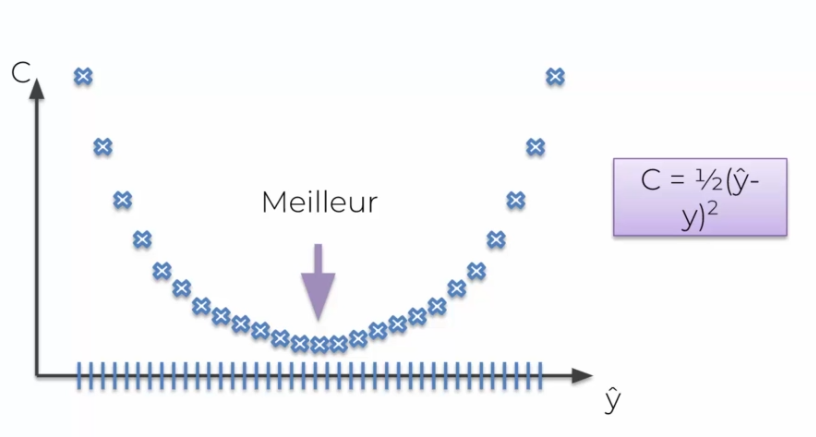
OK cela marche très bien pour un poids, mais lorsque l'on a plusieurs poids, on est touché par le fléau de la dimension. Mais comment faire pour minimiser une fonction de couts ? C'est-à-dire pour plein de fonctions de poids ?

Supposons que l'on essaie 1000 valeurs par poids, ce qui fait énormément de combinaisons finales. Il est actuellement impossible de le calculer, avec un système de brut force, par le meilleur ordinateur du monde.

Pour ce faire, nous avons besoin de l'algorithme du gradient. On fait des tests en positif et négatifs (certaines itérations) pour optimiser le réseau de neurones, au lieu de tout tester un par un. On fait des itérations jusqu'à trouver la meilleure valeur. Ainsi on solutionne énormément de soucis de calcul et on arrive en seulement quelques itérations à la solution optimale.

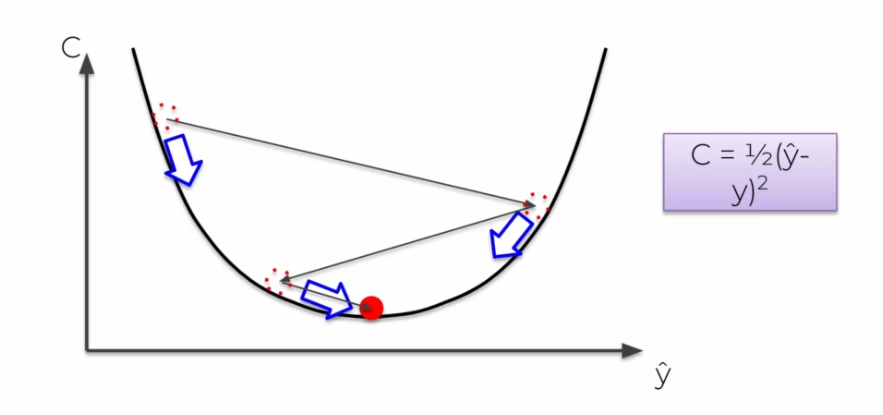
L'algorithme du gradient stochastique

Il existe un souci à l'algorithme du gradient, nous avons besoin d'une courbe dite convexe pour quelle fonctionne. Dans le cas contraire, on aura alors un minimum local dans certains cas qui ne sera pas un minimum global.

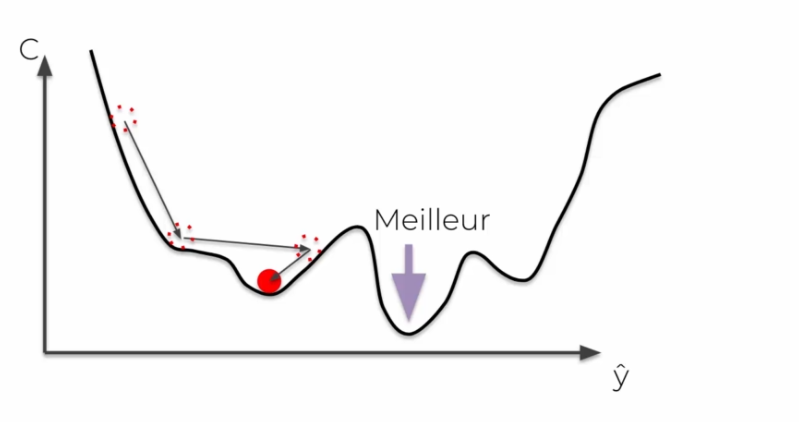
Dans le cas stochastique, on ajoute le cout directement ligne par ligne, ainsi au lieu de faire une somme finale des couts, à chaque itération les poids sont mis à jour. On évite alors de tomber sur des minimums globaux, il évite une fluctuation. Il sera aussi + rapide, et sera moins déterministe que le gradient par lot.

Résumons l'entrainement

• Étape 1 : initialisation des poids avec des valeurs proches du 0 (mais pas 0)
• Étape 2 : Envoi la première observation dans la couche d'entrée, avec une variable par neurone
• Étape 3 : Propagation avant ( de gauche à droite ) : Les neurones sont activés par dépendance au poids qui leur est attribuée. Propagez les activations jusqu'à obtenir la prédiction ^Y
• Étape 4 : On compare la prédiction avec la vraie valeur et on mesure l'erreur par une fonction de coût
• Étape 5: Retropropagation (de droite à gauche) : l'erreur se repropage dans le réseau, on met à jour les poids selon leur responsabilité dans l'erreur.
• Étape 6 : On répète les étapes 1 à 5
• Étape 7 : Quand toutes les données sont passées dans l'ANN, ça fait une époque. On refait alors plus d'époques. On améliore alors le réseau de neurones.

Régression et Classification

Régression simple

Prenons comme exemple : Y (variable dépendante) est le salaire d'un employé, qu'elle est la donnée (variable indépendante ou X1) qui fait varier cet Y. ainsi

• Y : est le salaire
• X1 : l'âge de l'employé, celui qui fait monter son salaire
• B1: le coefficient de X1, cela montre comment X affecte Y
• B0 : c'est une constante

On collecte plusieurs données en fonction des années des individus. Prenons les exemples suivants :

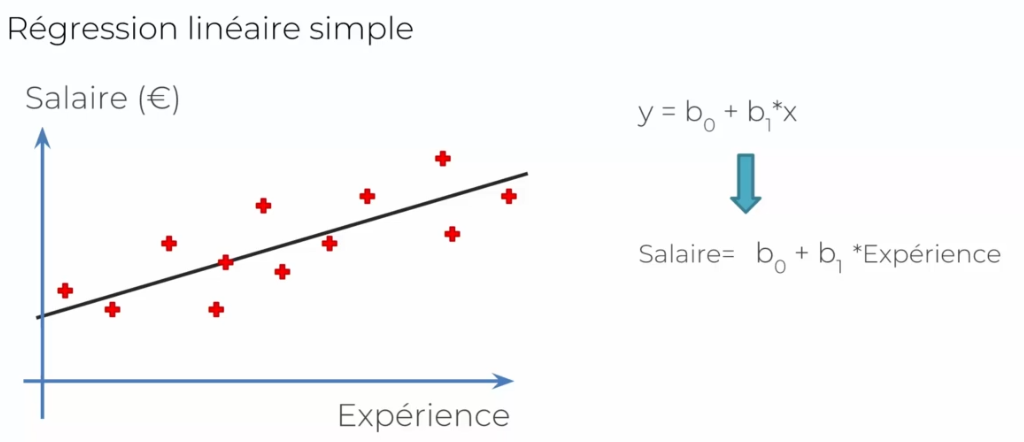
On a donc une droite dans le graphe qui caractérise notre norme que l'on cherche. Dans le cas actuel, on trace simplement une droite le plus au milieu possible. Regardons-le du côté de ^Y (prédiction) et de la vraie valeur :

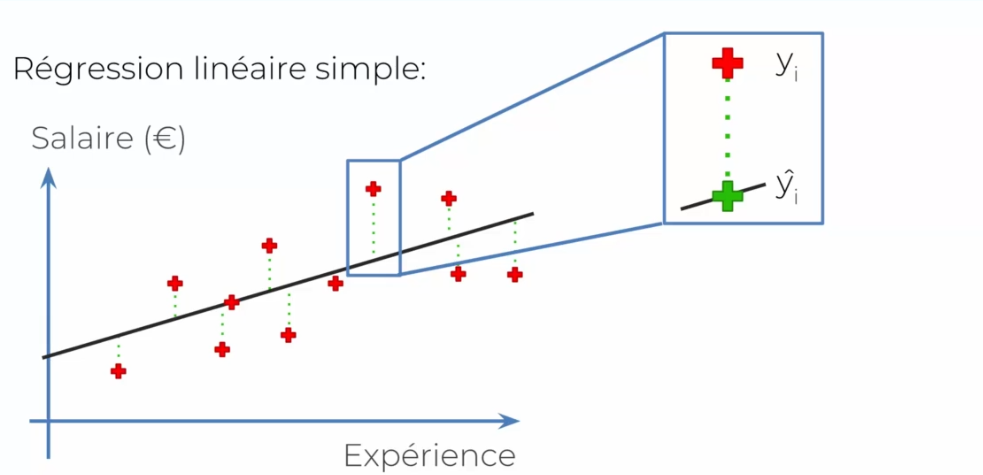
Dans le cas présent, tracer une droite risque d'être complexe. On aura jamais une réponse dite pertinente par une droite tracée au milieu :

Régression multiple

La méthode est la même, seulement la formule change :

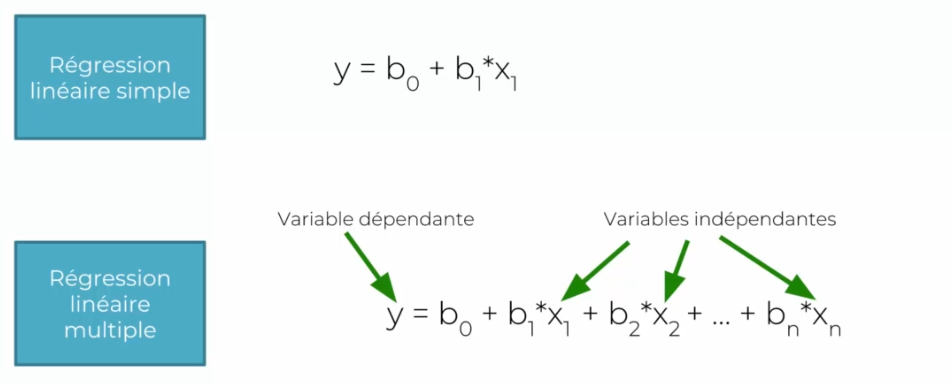
Régression logistique

Supposons qu'une entreprise envoie des emails à des clients et via cet email le client achète ou pas l'offre émise :

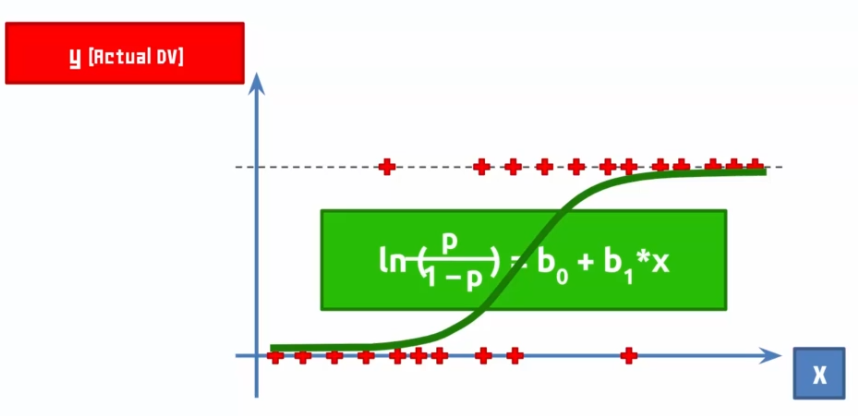
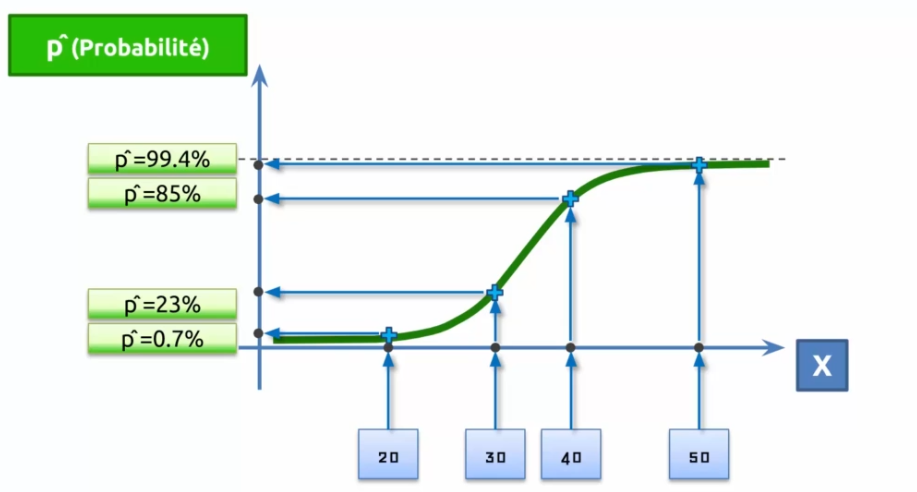
Ainsi on trace une courbe qui tente à minimiser les erreurs, cette courbe est notre modèle ! Si l'on parle de probabilité en axe Y, on dira que plus la courbe est proche de Y, plus il est probable que notre prédiction soit vraie.

Entrainer un réseau de neurones

1. Initialiser les poids avec des valeurs proches du 0 (mais différent de 0)
2. Envoyer la première observation dans la couche d'entrée, avec une variable par neurone
3. Propagation avant (de gauche à droite): Les neurones sont activés d'une manière dépendant, des poids qui leur sont attribués. Propagez les activations jusqu'à obtenir la prédiction y.
4. Comparer la prédiction avec la vraie valeur et mesurer l'erreur avec la fonction de cout
5. Propagation arrière (de droite à gauche): L'erreur se repropage dans le réseau. Mettre à jour les poids selon leur responsabilité dans l'erreur. Le taux d'apprentissage détermine de combien on ajuste les poids.
6. Répéter les étapes 1 à 5 et ajuster les poids après chaque observation (apprentissage renforcé) ou répéter étapes 1à5 et ajuster les poids après un lot d'observations (apprentissage par lot)
7. Quand tout le jeu de données est passé à travers l'ANN, on crée alors une époque. On refait plus d'une époque.

Évaluer un réseau de neurones

Lorsque l'on évalue plusieurs fois un réseau de neurones, on remarque que le pourcentage de réussite varie. Cela vient du juste milieu entre le biais et la variance :

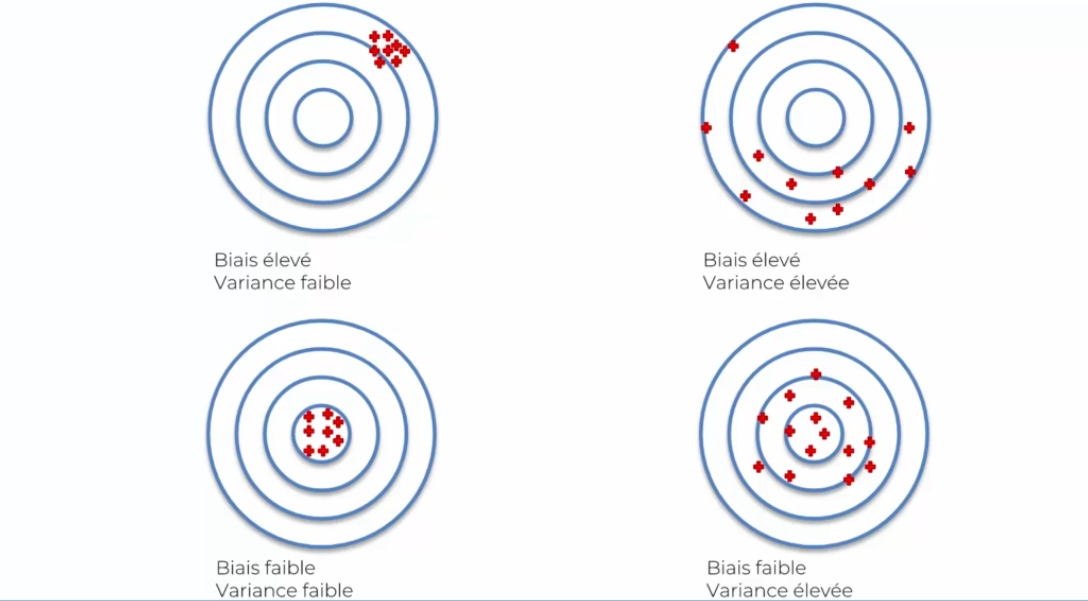
Une bonne manière d'évaluer un modèle est de l'évaluer en regardant les résultats via les tests et les résultats émis. Mais ce n'est pas la meilleure, car on aura ce souci de variance importante. On va donc devoir trouver une autre solution : le K-fold cross validation !

• On va prendre notre jeu de données que l'on ne divisera pas en données d'entrainement et de test
• On va diviser ces données en 10 parties qui représenteront notre jeu de données !
• À chaque itération, on prendra 9 parties pour notre entrainement et 1 pour notre test
• Ainsi à chaque itération les données changent et on a des jeux de données constamment différentes

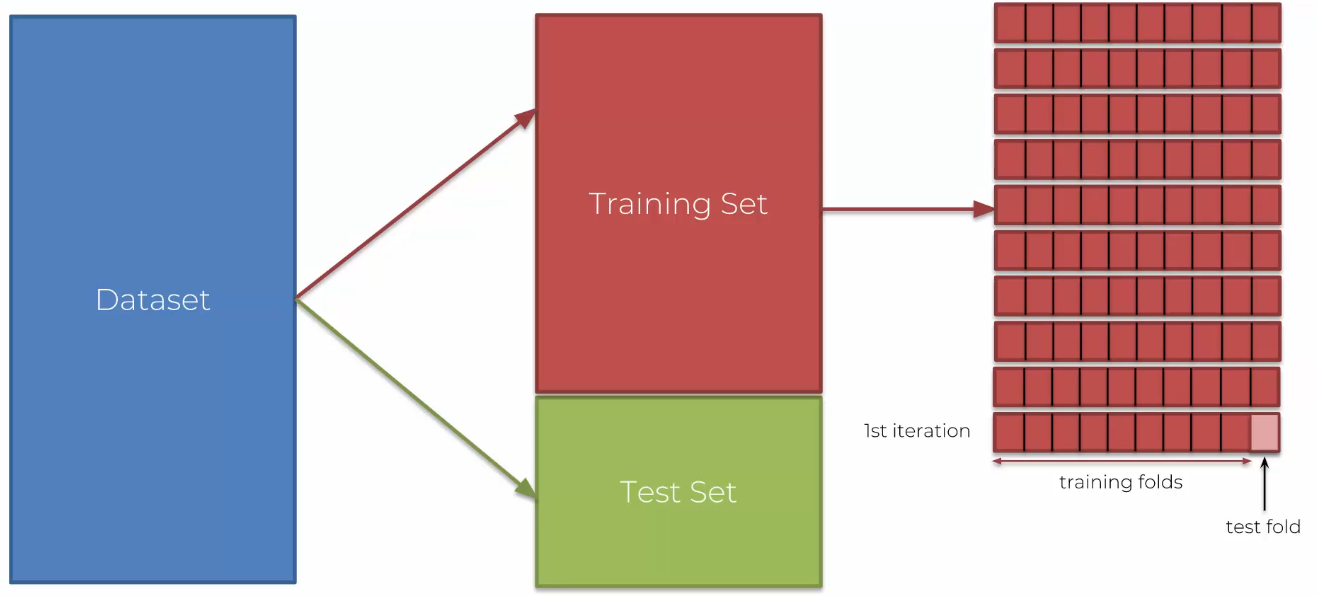
• On aura donc 10 valeurs pour la précision, mais aussi : des valeurs + précises, une idée de l'écart type de la valeur (toute proche de la moyenne). On saura alors si on est proche de la variance, l'objectif étant d'avoir une variance faible et un biais faible (précision).

Une chose qui est importante à comprendre est qu'un réseau de neurones peut être en surapprentissage. L'une des manières de résoudre ce souci est d'utiliser : classifier.add(Dropout(0.1)) qui permet d'ajouter une variable de chance où un neurone peut être retiré afin d'ajouter plus de complexité et donc éviter qu'un neurone s'habitude trop à des résultats.

Ajuster un réseau de neurones

Lors de la création d'un réseau, bien souvent on pense que le premier réseau créé est le bon. Mais un réseau peut toujours être amélioré en lui changeant et testant des paramètres. Comme :

• Ajouter ou retirer des neurones
• Tester d'autres fonctions d'activation Pour ce faire une solution existe : Grid search. Cet algorithme permet de tester plusieurs possibilités des paramètres, pour ensuite sortir la meilleure des comparaisons.