Introduction

La détection d'anomalies est une technique d'apprentissage automatique utilisée pour identifier des événements inhabituels ou anormaux dans un ensemble de données d'événements normaux qui ne sont pas étiquetés. L'algorithme apprend à détecter les anomalies en analysant un ensemble de fonctionnalités dans les données et en levant un drapeau rouge si le nouvel événement semble différent des précédents. Par exemple, la détection d'anomalies peut être utilisée pour détecter les défauts dans les moteurs d'avion après leur fabrication, afin d'éviter des défaillances potentielles qui peuvent avoir des conséquences négatives.

Pour illustrer le fonctionnement de la détection d'anomalies, considérons un ensemble de données de moteurs d'avion avec deux fonctionnalités : la chaleur générée (x1) et l'intensité des vibrations (x2). Lorsqu'un nouveau moteur d'avion est produit, l'algorithme calcule les valeurs de x1 et x2 pour le nouveau moteur et les représente graphiquement aux côtés des moteurs précédents. Si le nouveau moteur se situe dans la plage de valeurs vues auparavant, l'algorithme le considère comme normal et ne lève pas de drapeau. Cependant, si le nouveau moteur a une signature de chaleur et de vibration significativement différente, l'algorithme l'identifie comme une anomalie et recommande une inspection supplémentaire.

La méthode la plus courante pour effectuer la détection d'anomalies est l'estimation de densité, où l'algorithme construit un modèle de la distribution de probabilité des fonctionnalités dans l'ensemble de données. L'algorithme apprend à reconnaître les régions de données ayant une probabilité plus élevée ou plus faible et utilise cette information pour identifier les anomalies. Lorsqu'un nouvel événement est rencontré, l'algorithme calcule sa probabilité en fonction du modèle et la compare à une petite valeur seuil (epsilon). Si la probabilité est inférieure à epsilon, l'algorithme lève un drapeau pour une anomalie.

La détection d'anomalies est utilisée dans diverses applications, telles que la détection de fraudes, la fabrication et la surveillance informatique. Dans la détection de fraudes, l'algorithme peut être utilisé pour identifier des modèles inhabituels dans l'activité de l'utilisateur, tels que la fréquence de connexion inhabituelle ou le volume de transactions, qui peuvent indiquer un comportement frauduleux. Dans la fabrication, l'algorithme peut être utilisé pour identifier des pièces anormales, telles que des cartes de circuits imprimés ou des smartphones défectueux, afin d'éviter d'expédier des produits défectueux aux clients. Dans la surveillance informatique, l'algorithme peut identifier des comportements anormaux dans une machine, tels qu'une utilisation élevée de la mémoire ou de la charge CPU, qui peuvent indiquer une défaillance ou une violation de sécurité.

La détection d'anomalies est un outil puissant pour identifier des événements inhabituels dans un ensemble de données d'événements normaux, et elle est largement utilisée dans de nombreuses industries. Bien que l'algorithme ne soit pas souvent discuté, il est une partie essentielle de la boîte à outils de l'apprentissage automatique pour détecter les anomalies et améliorer le contrôle de la qualité.

Gaussian

La détection d'anomalies est une technique couramment utilisée dans l'analyse de données pour identifier les instances inhabituelles ou anormales dans un ensemble de données. La première étape de ce processus consiste à modéliser la distribution des données, et la distribution gaussienne (également appelée distribution normale) est un choix populaire à cet égard. En fait, la courbe en forme de cloche que vous avez peut-être entendue parler fait référence à la distribution gaussienne.

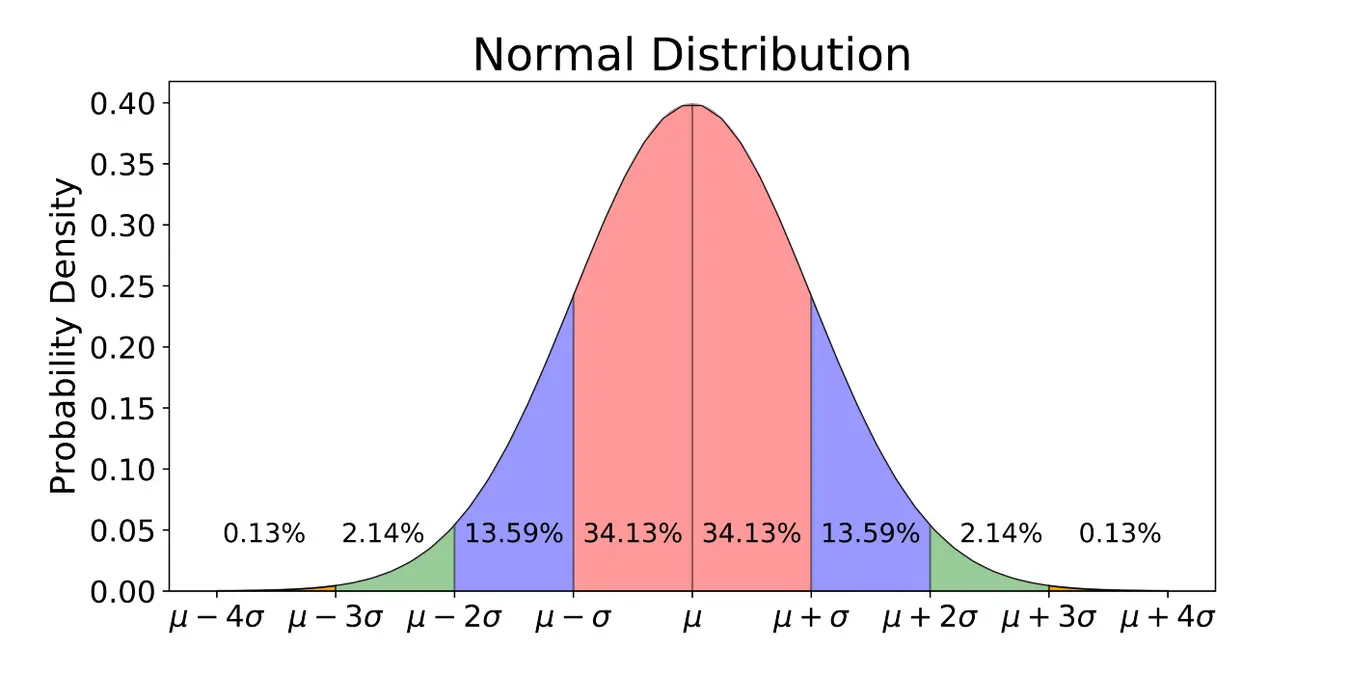
Lorsque l'on modélise les données en utilisant la distribution gaussienne, on suppose que les données suivent une distribution de probabilité décrite par une courbe en forme de cloche. Le centre de cette courbe, appelé paramètre de moyenne µ, représente la valeur la plus probable des données. L'écart-type de la courbe, indiqué par Sigma, décrit la dispersion des données autour de la moyenne. La courbe est mathématiquement représentée par la fonction de densité de probabilité (PDF) :

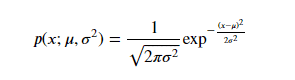
Pour appliquer la détection d'anomalies en utilisant la distribution gaussienne, nous devons estimer les valeurs de µ et Sigma qui décrivent le mieux les données. Nous le faisons en utilisant la méthode d'estimation du maximum de vraisemblance, où µ est estimé comme la moyenne des exemples d'entraînement et Sigma est estimé comme la moyenne de la différence au carré entre les exemples d'entraînement et la valeur estimée de µ.:

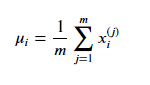
Une fois que nous avons estimé ces paramètres, nous pouvons utiliser la PDF pour calculer la probabilité qu'une nouvelle instance soit un point de données normal ou anormal.

En pratique, les ensembles de données ont généralement plusieurs caractéristiques, et nous devons étendre la distribution gaussienne pour gérer ce cas. Pour ce faire, nous supposons que chaque caractéristique suit une distribution gaussienne avec sa propre moyenne et son propre écart-type. Nous pouvons ensuite combiner ces distributions pour former une distribution gaussienne multivariée qui modélise la probabilité conjointe de toutes les caractéristiques. La PDF pour une distribution gaussienne multivariée est donnée par :

p(x) = (1 / ((2 * pi)^(n/2) * det(Sigma)^0.5)) * exp(-0.5 * (x - µ)' * inv(Sigma) * (x - µ)),

où n est le nombre de caractéristiques, µ est un vecteur de moyennes, Sigma est une matrice de covariance, et inv(Sigma) est l'inverse de Sigma :

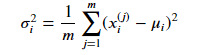
En résumé, la distribution gaussienne est un outil utile pour modéliser la distribution de données dans la détection d'anomalies. En estimant la moyenne et l'écart-type de la distribution, nous pouvons identifier les instances anormales dans un ensemble de données. La distribution gaussienne multivariée étend ce concept aux ensembles de données avec plusieurs caractéristiques, nous permettant de modéliser la probabilité conjointe de toutes les caractéristiques.

Algorithme

Pour construire un algorithme de détection d'anomalies, la première étape consiste à sélectionner les caractéristiques xi qui pourraient être indicatives d'exemples anormaux. Nous estimons ensuite les paramètres µ1 à µn et Sigma²1 à Sigma²n pour les n caractéristiques de notre ensemble de données en utilisant la méthode d'estimation du maximum de vraisemblance.

Le modèle de p(x), la probabilité de tout vecteur de caractéristiques donné, est alors calculé comme le produit de la probabilité de chaque caractéristique individuelle en utilisant la distribution Gaussienne. Si nous avons n caractéristiques, alors le produit de la probabilité de chaque caractéristique peut être écrit comme le produit de j = 1 à n de p(xj) avec les paramètres µj et Sigma²j.

Une fois que nous avons estimé ces paramètres, nous pouvons calculer p(x) pour un nouvel exemple x et le comparer à une valeur de seuil prédéfinie epsilon. Si p(x) est inférieur à epsilon, nous signalons l'exemple comme une anomalie.

L'intuition derrière cet algorithme est qu'il a tendance à signaler un exemple comme anormal si une ou plusieurs caractéristiques sont très grandes ou très petites par rapport à ce qu'il a vu dans l'ensemble de formation. Cela se fait en ajustant une distribution Gaussienne pour chaque caractéristique xj et en vérifiant si la probabilité de la caractéristique individuelle est faible.

Pour choisir le paramètre epsilon, nous utilisons généralement un ensemble de validation et sélectionnons la valeur qui nous donne le meilleur compromis entre les faux positifs et les faux négatifs.

La détection d'anomalies en utilisant la distribution Gaussienne est un outil utile pour identifier les instances anormales dans un ensemble de données. En estimant la moyenne et l'écart-type de la distribution pour chaque caractéristique individuelle, nous pouvons signaler des exemples qui sont statistiquement différents de l'ensemble de formation.

Développer et évaluer un système

Dans le développement d'un système, la capacité de l'évaluer au fur et à mesure de son avancement peut grandement faciliter la prise de décisions et l'amélioration du système. Cela est particulièrement vrai dans le développement d'algorithmes d'apprentissage. Par exemple, lors du développement d'un algorithme d'apprentissage, il peut être nécessaire de prendre des décisions sur la sélection de fonctionnalités ou le choix de valeurs pour des paramètres tels que epsilon. S'il existe un moyen d'évaluer l'algorithme pendant le développement, tel que par une évaluation de nombres réels, le processus de prise de décision devient beaucoup plus simple. L'évaluation de nombres réels implique la capacité de changer rapidement l'algorithme et de calculer un nombre qui indique si le changement a rendu l'algorithme meilleur ou pire.

La détection d'anomalies est un exemple d'application où l'évaluation de nombres réels est particulièrement utile. Bien que nous ayons principalement parlé de données non étiquetées, il est possible d'incorporer des données étiquetées dans le processus de détection d'anomalies. En utilisant un petit nombre d'exemples anormaux étiquetés, on peut créer un ensemble de validation croisée qui peut être utilisé pour évaluer l'algorithme. L'ensemble de validation croisée comprend à la fois des exemples normaux et anormaux, et l'algorithme est entraîné sur un ensemble séparé d'exemples normaux.

Par exemple, considérons la détection d'anomalies dans les moteurs d'avion. Supposons que nous avons collecté des données de 10 000 bons moteurs et de 20 moteurs anormaux. Nous pouvons diviser ces données en un ensemble d'entraînement, un ensemble de validation croisée et un ensemble de test. L'ensemble d'entraînement comprend 6 000 bons moteurs, et l'ensemble de validation croisée comprend 2 000 bons moteurs et 10 moteurs anormaux. L'ensemble de test comprend 2 000 bons moteurs et 10 moteurs anormaux.

L'algorithme est entraîné sur l'ensemble d'entraînement en ajustant les distributions gaussiennes aux exemples normaux. L'ensemble de validation croisée est ensuite utilisé pour régler le paramètre epsilon et évaluer la capacité de l'algorithme à identifier correctement les moteurs anormaux. L'algorithme est ensuite évalué sur l'ensemble de test pour déterminer sa performance.

Lors de l'évaluation de l'algorithme, une évaluation de nombres réels est effectuée en calculant p(x), la probabilité qu'un exemple donné x soit normal, et en la comparant à une valeur choisie d'epsilon. Si p(x) est inférieur à epsilon, l'exemple est identifié comme anormal. L'évaluation est généralement réalisée en utilisant des métriques telles que la précision, le rappel, le score F1 ou la précision de classification, en particulier lorsque la distribution d'exemples positifs et négatifs est fortement déséquilibrée.

Bien que des données étiquetées puissent être utilisées dans la détection d'anomalies, il s'agit toujours principalement d'un algorithme d'apprentissage non supervisé. Cependant, l'intégration d'exemples étiquetés dans le processus d'évaluation peut grandement faciliter le développement de l'algorithme. Malgré cela, il peut être tentant d'utiliser un algorithme d'apprentissage supervisé lorsque des exemples étiquetés sont disponibles. Cependant, les algorithmes d'apprentissage non supervisés sont toujours préférés car ils ne nécessitent pas de jeu de données étiquetées pour l'entraînement, ce qui peut être difficile à obtenir pour certaines applications.

Quelles features utilisées

En apprentissage automatique, la sélection de fonctionnalités est l'un des aspects essentiels pour construire des modèles efficaces. En particulier, le choix du bon ensemble de fonctionnalités est crucial pour la détection d'anomalies, où le modèle apprend uniquement à partir de données non étiquetées. Dans cet article de blog, nous explorerons quelques astuces pratiques pour la sélection de fonctionnalités dans la détection d'anomalies.

L'importance des fonctionnalités gaussiennes

Une façon de s'assurer que vos fonctionnalités sont adaptées à la détection d'anomalies est de veiller à ce qu'elles soient approximativement gaussiennes. Les fonctionnalités gaussiennes ont l'avantage d'être symétriques et unimodales, ce qui les rend plus faciles à modéliser à l'aide de distributions de probabilité comme la distribution normale. En revanche, les fonctionnalités non gaussiennes peuvent être plus difficiles à modéliser et peuvent nécessiter des transformations complexes pour être utilisées de manière appropriée dans un modèle.

Prenons l'exemple d'une fonctionnalité X. Pour vérifier si elle est gaussienne, nous pouvons tracer un histogramme de X en utilisant la commande Python plt.hist(X). Si l'histogramme ressemble à une courbe en forme de cloche symétrique, la fonctionnalité est probablement gaussienne. Cependant, si l'histogramme n'est pas symétrique, la fonctionnalité est non gaussienne et nécessite une transformation.

Transformation de fonctionnalités non gaussiennes

L'une des façons les plus courantes de transformer des fonctionnalités non gaussiennes consiste à prendre le logarithme de la fonctionnalité. Cette transformation est utile pour les fonctionnalités qui ont une longue queue vers des valeurs plus élevées, ce qui les rend non gaussiennes. En appliquant le logarithme, nous pouvons comprimer la queue et rendre la fonctionnalité plus symétrique.

Une autre façon de transformer des fonctionnalités non gaussiennes consiste à les élever à une puissance fractionnaire. Par exemple, nous pouvons prendre la racine carrée d'une fonctionnalité X en utilisant la commande Python np.sqrt(X) pour créer une nouvelle fonctionnalité. Cette transformation est utile pour les fonctionnalités qui ont une longue queue vers des valeurs plus basses.

Prenons l'exemple d'une fonctionnalité non gaussienne X1 qui a une longue queue vers des valeurs plus élevées. Pour transformer X1, nous pouvons appliquer la transformation logarithmique en utilisant la commande Python np.log(X1). Nous pouvons ensuite tracer l'histogramme de la fonctionnalité transformée en utilisant plt.hist(np.log(X1)). Si l'histogramme ressemble plus à une distribution gaussienne, nous pouvons utiliser la fonctionnalité transformée dans notre modèle au lieu de la fonctionnalité d'origine.

De même, prenons un autre exemple de fonctionnalité non gaussienne, X2, qui présente une longue queue vers des valeurs inférieures. Pour transformer X2, nous pouvons prendre sa racine carrée en utilisant la commande Python np.sqrt(X2). Nous pouvons ensuite tracer l'histogramme de la fonctionnalité transformée en utilisant plt.hist(np.sqrt(X2)). Si l'histogramme semble plus gaussien, nous pouvons utiliser la fonctionnalité transformée dans notre modèle plutôt que la fonctionnalité originale.

Exploration de différentes transformations

En pratique, il peut être nécessaire d'essayer plusieurs transformations différentes pour trouver celle qui convient le mieux à nos données. Par exemple, nous pouvons essayer différentes valeurs de la puissance fractionnelle pour une fonctionnalité ou différentes valeurs de base pour les transformations logarithmiques.

Pour explorer différentes transformations, nous pouvons tracer l'histogramme de chaque fonctionnalité transformée en utilisant plt.hist(fonctionnalité transformée), où fonctionnalité transformée est le résultat de l'application d'une transformation spécifique à la fonctionnalité originale. En visualisant les histogrammes, nous pouvons sélectionner la transformation qui produit la fonctionnalité la plus gaussienne.

Réalisation d'une analyse d'erreur

Même avec des fonctionnalités gaussiennes, les modèles de détection d'anomalies ne détectent pas toujours les anomalies avec précision. Dans de tels cas, il est utile de réaliser une analyse d'erreur pour identifier les types d'anomalies que le modèle ne parvient pas à détecter. En fonction des résultats de l'analyse d'erreur, nous pouvons générer de nouvelles fonctionnalités pour distinguer les exemples normaux des exemples anormaux.

Par exemple, supposons que nous construisions un système de détection d'anomalies pour surveiller les ordinateurs dans un centre de données. Nous pourrions commencer par des fonctionnalités telles que l'utilisation de la mémoire, les accès au disque par seconde, la charge du processeur et le volume du trafic réseau. Si le modèle ne parvient pas à détecter certaines anomalies, nous pouvons créer de nouvelles fonctionnalités en combinant les anciennes ou en en introduisant de nouvelles. Par exemple, nous pouvons calculer le rapport entre la charge du processeur et le volume de trafic réseau, ou le carré de la charge du processeur divisé par le volume de trafic réseau. En procédant ainsi, nous pouvons créer une nouvelle fonctionnalité qui est plus sensible à des types spécifiques d'anomalies.

Une fois que nous avons créé de nouvelles fonctionnalités, nous devons mettre à jour notre modèle de détection d'anomalies en y incorporant les nouvelles fonctionnalités. Nous pouvons ensuite évaluer les performances du modèle mis à jour en comparant ses prédictions avec les anomalies réelles de notre ensemble de données. Cela nous aidera à déterminer si les nouvelles fonctionnalités ont amélioré les performances de notre modèle.

En conclusion, le choix attentif des caractéristiques est crucial pour la construction d'un système efficace de détection d'anomalies. Il est particulièrement important de veiller à ce que les caractéristiques soient approximativement gaussiennes, car cela peut améliorer considérablement les performances du modèle. Si le modèle ne détecte pas les anomalies avec précision, nous pouvons effectuer une analyse des erreurs pour identifier les types d'anomalies qui ne sont pas détectées et créer de nouvelles caractéristiques pour combler ces lacunes. En affinant de manière itérative les caractéristiques et le modèle, nous pouvons construire un système de détection d'anomalies robuste et précis.