Introduction au fonctions d'activations

Lorsque l'on construit des réseaux de neurones, il est courant d'utiliser la fonction d'activation sigmoïde dans tous les nœuds des couches cachées et de la couche de sortie. Cependant, l'utilisation de différentes fonctions d'activation peut rendre un réseau de neurones beaucoup plus performant. Dans cet article, nous allons discuter de la façon d'utiliser différentes fonctions d'activation et de leur impact sur les performances d'un réseau de neurones.

Les fonctions d'activation

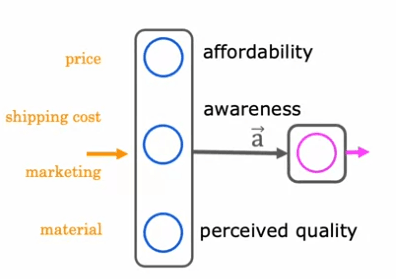
Prenons un exemple de prédiction des articles les plus vendus en fonction de facteurs tels que le prix, les coûts d'expédition, la publicité et la matière. Cet exemple suppose que la sensibilisation au produit est binaire - soit les gens sont conscients, soit ils ne le sont pas. Cependant, il est possible que le degré de sensibilisation ne soit pas binaire et puisse être un nombre non négatif.

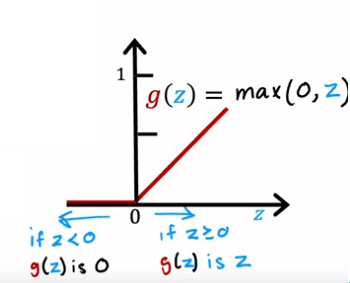
Pour résoudre ce problème, nous pouvons utiliser une fonction d'activation différente qui permet une plus large gamme de valeurs. Une fonction d'activation très courante utilisée dans les réseaux de neurones est la fonction d'activation linéaire rectifiée (ReLU), qui est définie comme g(z) = max (0, z). Cette fonction est utile car elle permet des valeurs non négatives et peut mieux modéliser la sensibilisation en tant que variable continue.

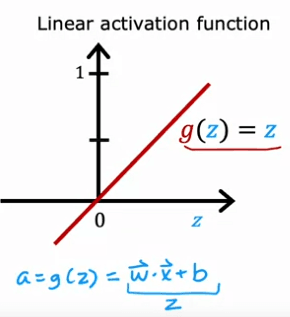
Une autre fonction d'activation couramment utilisée est la fonction d'activation linéaire, qui est définie comme g(z) = z. Bien que cette fonction n'introduise aucune non-linéarité, elle peut être utile dans certaines situations.

Quelles conclusion pouvons nous en tirer ?

En conclusion, le choix de la fonction d'activation peut avoir un impact significatif sur les performances d'un réseau de neurones. La fonction sigmoïde, ReLU et la fonction d'activation linéaire sont certaines des fonctions les plus couramment utilisées dans l'apprentissage profond. Il est important de tester différentes fonctions d'activation pour trouver celle qui convient le mieux à votre problème spécifique. De plus, comprendre les mathématiques derrière ces fonctions et l'impact sur le réseau de neurones peut vous aider à prendre de meilleures décisions lors de la conception d'un réseau de neurones.

Comment choisir ?

En ce qui concerne la fonction d'activation de la couche de sortie, il est important de considérer le type de problème que vous essayez de résoudre. Par exemple, si vous travaillez sur un problème de classification binaire où l'étiquette cible est soit zéro soit un, la fonction d'activation sigmoïde est souvent le choix le plus naturel. Cela est dû au fait que le réseau neuronal apprend à prédire la probabilité que l'étiquette soit égale à un, similaire à la régression logistique.

D'un autre côté, si vous résolvez un problème de régression, comme prévoir la variation du cours de l'action de demain, une fonction d'activation linéaire peut être un meilleur choix. Cela est dû au fait que la sortie du réseau neuronal peut prendre des valeurs positives ou négatives.

Pour les couches cachées, le choix le plus courant de fonction d'activation est la fonction d'activation linéaire rectifiée (ReLU). C'est parce que la fonction ReLU est plus rapide à calculer et s'est avérée efficace dans de nombreuses situations. De plus, la fonction ReLU devient plate uniquement dans une partie du graphique, tandis que la fonction d'activation sigmoïde devient plate à deux endroits, ce qui peut ralentir le processus d'apprentissage.

Le choix de la fonction d'activation peut avoir un impact significatif sur les performances d'un réseau neuronal. Il est important de tester différentes fonctions d'activation pour trouver la meilleure pour votre problème spécifique. Comprendre les mathématiques derrière ces fonctions et leur impact sur le réseau neuronal peut également vous aider à prendre de meilleures décisions lors de la conception d'un réseau neuronal.

Pourquoi avons nous besoin de ces fonctions

Les réseaux de neurones sont des modèles d'apprentissage automatique puissants qui sont utilisés pour résoudre une variété de problèmes, tels que la classification d'images, le traitement du langage naturel et la prédiction de la demande. Cependant, pour que le réseau neuronal fonctionne efficacement, il doit avoir des fonctions d'activation en place. Une fonction d'activation est une fonction mathématique qui est appliquée à la sortie d'un neurone, ce qui aide à introduire une non-linéarité dans le modèle.

L'une des raisons les plus importantes d'utiliser des fonctions d'activation est qu'en l'absence de celles-ci, un réseau neuronal ne serait plus différent d'un modèle de régression linéaire. Cela est dû à la fonction d'activation linéaire, qui est représentée par l'équation g(z) = z, qui n'introduit pas de non-linéarité dans le modèle.

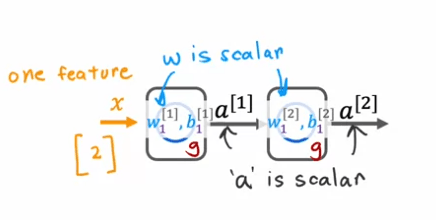
Pour illustrer cela, considérons un exemple simple d'un réseau neuronal avec une unité cachée et une unité de sortie. L'entrée x est un nombre, et l'unité cachée a des paramètres w1 et b1 qui produisent a1, qui est également un nombre. L'unité de sortie a des paramètres w2 et b2 et produit a2, qui est la sortie finale du réseau neuronal.

Si nous utilisions la fonction d'activation linéaire partout dans ce réseau neuronal, le calcul de a1 serait représenté par l'équation a1 = g(w1x + b1), mais étant donné que g(z) = z, cela est équivalent à w1x + b1. De manière similaire, le calcul de a2 serait représenté par l'équation a2 = g(w2a1 + b2), ce qui se simplifie en w2w1x + w2b1 + b2.

Si nous simplifions cela encore plus, nous pouvons voir que a2 est simplement une fonction linéaire de l'entrée x, ce qui signifie que ce réseau neuronal n'est pas différent d'un modèle de régression linéaire. C'est pourquoi avoir plusieurs couches dans un réseau neuronal ne permet pas au réseau neuronal de calculer des caractéristiques plus complexes ou d'apprendre quelque chose de plus complexe qu'une fonction linéaire.

En général, si nous utilisions une fonction d'activation linéaire pour toutes les couches cachées et utilisions également une fonction d'activation linéaire pour la couche de sortie, alors la sortie a4 peut être exprimée comme une fonction linéaire des caractéristiques d'entrée x plus b. En alternative, si nous utilisions une fonction d'activation linéaire pour toutes les couches cachées, mais utilisions une fonction d'activation logistique pour la couche de sortie, alors le modèle devient équivalent à la régression logistique.

En conclusion, les fonctions d'activation sont cruciales pour les réseaux de neurones car elles introduisent une non-linéarité dans le modèle, ce qui est nécessaire pour que le réseau neuronal puisse apprendre des caractéristiques plus complexes. En pratique, la fonction d'activation ReLU est couramment utilisée dans les couches cachées, ce qui fonctionne bien dans la plupart des cas.

Multiclass

La classification multiclasse est un type de problème de classification où il y a plus de deux étiquettes de sortie possibles. Cela signifie qu'au lieu d'avoir seulement deux options, comme zéro ou un, il peut y avoir plusieurs classes à choisir.

Par exemple, dans un problème de classification de chiffres manuscrits, nous pourrions vouloir reconnaître tous les 10 chiffres au lieu de seulement 0 et 1. Ou en diagnostic médical, nous pourrions vouloir classer les patients avec l'un des trois ou cinq différentes maladies possibles. Cela serait également un problème de classification multiclasse.

Dans un problème de classification multiclasse, la variable de sortie y ne peut prendre qu'un petit nombre de catégories discrètes, mais maintenant y peut prendre plus de deux valeurs possibles.

En opposition aux problèmes de classification binaires, où nous aurions un jeu de données avec des caractéristiques x1 et x2, dans les problèmes de classification multiclasse, nous aurions un jeu de données qui ressemble à cela avec plusieurs classes représentées par des symboles différents. Au lieu d'estimer la probabilité de y égal à 1, nous voudrions estimer la probabilité de y égal à l'un des classes possibles.

Softmax

L'algorithme de régression Softmax est une généralisation de la régression logistique, qui est un algorithme de classification binaire dans des contextes de classification multiclasse. En régression logistique, la variable de sortie y peut prendre deux valeurs de sortie possibles, soit zéro ou un. L'algorithme calcule d'abord z = w.produit de x + b, puis calcule a = g(z), qui est une fonction sigmoïde appliquée à z. Cela est interprété comme l'estimation de la régression logistique de la probabilité que y soit égal à 1 donné les caractéristiques d'entrée x.

Pour généraliser cela à la régression softmax, nous utiliserons un exemple concret où y peut prendre quatre sorties possibles, c'est-à-dire 1, 2, 3 ou 4. La régression softmax calculera z1 = w1.produit de x + b1, z2 = w2.produit de x + b2, et ainsi de suite pour z3 et z4. Ici, w1, w2, w3, w4 ainsi que b1, b2, b3, b4 sont les paramètres de la régression softmax.

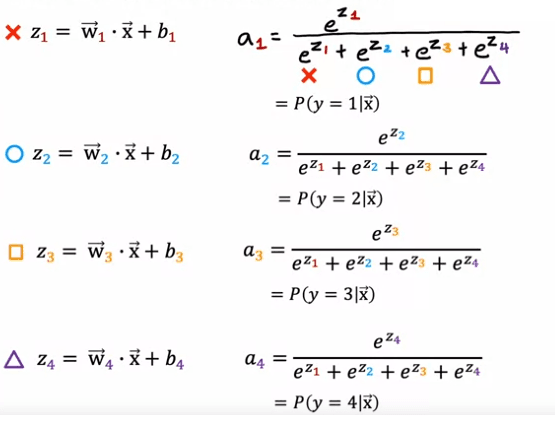
La formule pour la régression softmax est la suivante: a1 = e^z1/ (e^z1 + e^z2 + e^z3 + e^z4), et cela sera interprété comme l'estimation de l'algorithme de la probabilité que y soit égal à 1 donné les caractéristiques d'entrée x. De manière similaire, a2 = e^z2 / (e^z1 + e^z2 + e^z3 + e^z4) sera l'estimation de la probabilité que y soit égal à 2 donné les caractéristiques d'entrée x. De manière similaire, a3 et a4 seront calculés comme e^z3 / (e^z1 + e^z2 + e^z3 + e^z4) et e^z4 / (e^z1 + e^z2 + e^z3 + e^z4) respectivement.

Il est important de noter que la somme de tous les a1, a2, a3, a4 sera égale à 1, car ils représentent les probabilités de y prenant les valeurs 1, 2, 3 ou 4 respectivement.

Dans le cas général, où y peut prendre n valeurs possibles, les formules pour la régression softmax peuvent s'exprimer comme suit: ai = e^zi / (e^z1 + e^z2 + ... + e^zn) pour i = 1, 2, 3, ..., n.

En résumé, la régression softmax est un algorithme de classification multiclasse qui estime la probabilité de la variable de sortie y prenant différentes valeurs donné les caractéristiques d'entrée x. Il a des paramètres w1 à wn et b1 à bn, et si des choix appropriés pour ces paramètres peuvent être appris, il peut prédire les chances de y étant 1, 2, 3, ..., n donné un ensemble de caractéristiques d'entrée x.

Il est important de noter que la somme de tous les a1, a2, a3, a4 sera égale à 1, car ils représentent les probabilités de y prenant les valeurs 1, 2, 3 ou 4 respectivement.

Dans le cas général, où y peut prendre n valeurs possibles, les formules pour la régression softmax peuvent s'exprimer comme suit: ai = e^zi / (e^z1 + e^z2 + ... + e^zn) pour i = 1, 2, 3, ..., n.

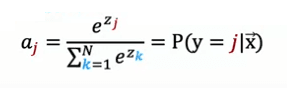
En résumé, la régression softmax est un algorithme de classification multiclasse qui estime la probabilité de la variable de sortie y prenant différentes valeurs donné les caractéristiques d'entrée x. Il a des paramètres w1 à wn et b1 à bn, et si des choix appropriés pour ces paramètres peuvent être appris, il peut prédire les chances de y étant 1, 2, 3, ..., n donné un ensemble de caractéristiques d'entrée x.

Comment l'appliquer

Pour construire un réseau de neurones capable de réaliser une classification multiclasse, nous allons utiliser le modèle de régression Softmax et l'intégrer dans la couche de sortie du réseau de neurones.

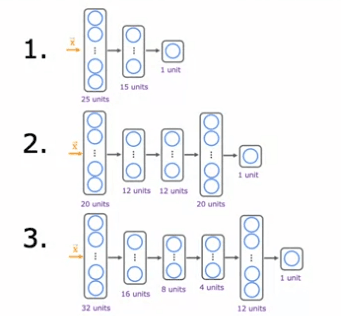
Auparavant, lorsque nous faisions la reconnaissance d'écriture manuscrite avec seulement deux classes, nous avons utilisé un réseau de neurones avec cette architecture. Si nous voulons maintenant faire une classification des chiffres manuscrits avec 10 classes, tous les chiffres de zéro à neuf, nous allons changer ce réseau de neurones pour avoir 10 unités de sortie. Et cette nouvelle couche de sortie sera une couche de sortie Softmax. Il arrive donc parfois que nous disions que ce réseau de neurones a une sortie Softmax ou que cette couche supérieure est une couche Softmax.

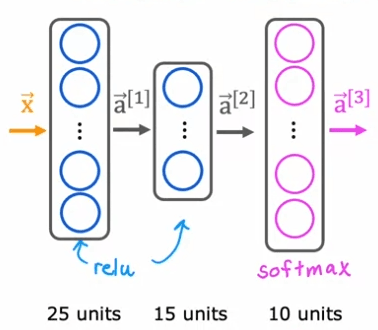
La façon dont la propagation avant fonctionne dans ce réseau de neurones est donnée par une entrée X, A1 est calculé exactement de la même manière qu'avant. Et puis A2, les activations pour la deuxième couche cachée sont également calculées de la même manière qu'avant. Et nous devons maintenant calculer les activations pour cette couche de sortie, qui est A3. Si vous avez 10 classes de sortie, nous allons calculer Z1, Z2 à Z10 en utilisant ces expressions. C'est donc en réalité très similaire à ce que nous avions précédemment pour la formule que vous utilisez pour calculer Z. Z1 est W1.produit avec A2, les activations de la couche précédente plus b1, et ainsi de suite pour Z1 à Z10. Ensuite, A1 est égal à e à Z1 divisé par e à Z1 plus jusqu'à e à Z10. Et c'est notre estimation de la probabilité que y soit égal à 1. Et de manière similaire pour A2 et de manière similaire jusqu'à A10.

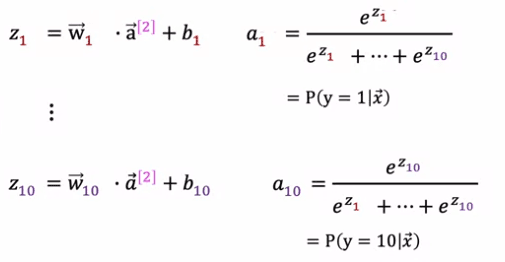
Il est important de noter que la somme de tous les a1, a2, a3, a4 sera égale à 1, car ils représentent les probabilités de y prenant les valeurs 1, 2, 3 ou 4 respectivement.

La couche Softmax sera parfois également appelée la fonction d'activation Softmax, elle est un peu inhabituelle à un égard par rapport aux autres fonctions d'activation que nous avons vues jusqu'à présent, comme sigma, radiale et linéaire, c'est que lorsque nous regardons les fonctions d'activation sigmoïde ou valeur ou linéaire, a1 était une fonction de Z1 et a2 était une fonction de Z2 et seulement Z2. En d'autres termes, pour obtenir les valeurs d'activation, nous pourrions appliquer la fonction d'activation g, qu'il s'agisse de sigmoïde ou rarement ou autre chose élément par élément à Z1 et Z2 et ainsi de suite pour obtenir a1 et a2 et a3 et a4. Mais avec la fonction d'activation Softmax, remarquez que a1 est une fonction de Z1 et Z2 et Z3 jusqu'à Z10. Ainsi, chacune de ces valeurs d'activation dépend de toutes les valeurs de Z.

Enfin, voyons comment vous pourriez le mettre en œuvre dans TensorFlow. Comme avant, il y a trois étapes pour spécifier et entraîner le modèle. La première étape consiste à dire à TensorFlow de chaîner séquentiellement trois couches. La première couche est ces 25 unités avec la fonction d'activation relu. La seconde couche est 15 unités de fonction d'activation relu. Et puis la troisième couche, car il y a maintenant 10 unités de sortie, vous voulez sortir a1 à a10, il y a donc maintenant 10 unités de sortie. Et nous dirons à TensorFlow d'utiliser la fonction d'activation Softmax.

 model = Sequential(
    [
        Dense(25, activation='relu', name = 'layer1'),
        Dense(15, activation='relu', name = 'layer2'),
        Dense(10, activation='softmax', name = 'layer3')
    ], name = "my_model"
)

Et la fonction coût sera la perte croisée d'entropie. La seconde étape consiste à entraîner le modèle à l'aide des données d'entraînement, et la dernière étape est d'évaluer les performances du modèle sur les données de test.

 model.compile(
    loss=SparseCategoricalCrossentropy())
)

model.fit(X,Y,epochs=100)

En résumé, pour construire un réseau neuronal qui peut effectuer une classification multi-classe, nous pouvons prendre le modèle de régression Softmax et le mettre dans la couche de sortie d'un réseau neuronal. La propagation avant fonctionne en calculant les activations pour la couche de sortie en utilisant la fonction d'activation Softmax. Cela nous donne des estimations de la probabilité de la variable de sortie y prenant des valeurs différentes en fonction des caractéristiques d'entrée x. La couche Softmax est unique en ce que chaque valeur d'activation dépend de toutes les valeurs de Z. Il peut être implémenté dans TensorFlow en spécifiant et en formant le modèle en utilisant les couches et la fonction d'activation appropriées.

Amélioration possible

Dans cette section, nous allons explorer l'importance de la stabilité numérique lors de la mise en œuvre d'algorithmes d'apprentissage automatique, en particulier dans le contexte de la régression logistique et de la régression softmax.

Tout d'abord, considérons un exemple de la façon dont les erreurs d'arrondissement numérique peuvent se produire dans les calculs. Lors du calcul de la valeur 2/10 000, nous avons deux options:

• Option 1: set x = 2/10,000.
• Option 2: set x =(1 + 1/10,000) -(1 -1/10,000).

Lorsque nous imprimons les résultats de ces options, nous pouvons voir que la deuxième option a une petite quantité d'erreur d'arrondissement. Cela est dû au fait que l'ordinateur a une quantité limitée de mémoire pour stocker chaque nombre, connu sous le nom de nombre à virgule flottante. Selon la façon dont nous décidons de calculer la valeur 2/10 000, le résultat peut avoir plus ou moins d'erreur d'arrondissement numérique.

Maintenant, examinons comment ces idées s'appliquent à la régression logistique. Dans la régression logistique, nous calculons la fonction de perte pour un exemple donné en calculant tout d'abord l'activation de sortie, a, qui est g (z) ou 1/(1 + e ^-z). Ensuite, nous calculons la perte en utilisant cette expression.

Dans l'implémentation traditionnelle, nous calculons a comme une valeur intermédiaire puis nous l'utilisons pour calculer la perte. Cependant, il s'avère que en spécifiant directement la fonction de perte (c'est-à-dire sans calculer a comme une valeur intermédiaire), TensorFlow peut réarranger les termes et calculer la fonction de perte de manière plus numériquement précise. Cela est réalisé en définissant la couche de sortie pour utiliser une fonction d'activation linéaire et en incluant à la fois la fonction d'activation et la perte de l'entropie croisée dans la spécification de la fonction de perte. Le code pour cette implémentation est montré ci-dessous:

 model.compile(loss=SparseCategoricalCrossEntropy(from_logits=True))

Bien que cette implémentation puisse être moins lisible, elle entraîne moins d'erreurs d'arrondi numérique. Dans le cas de la régression logistique, ces implémentations fonctionnent correctement, mais les erreurs d'arrondi numérique peuvent devenir pires lorsqu'il s'agit de softmax.

Pour améliorer la précision de notre implémentation de softmax, nous pouvons utiliser la même approche que celle que nous avons utilisée pour la régression logistique. Au lieu de calculer les activations en tant que termes intermédiaires séparés, nous pouvons spécifier directement la fonction de perte en fonction des valeurs de sortie.

Cela donne à TensorFlow la flexibilité de réarranger les termes et de calculer la fonction de perte de manière plus numériquement précise. Le code pour cela est montré comme suit: dans la couche de sortie, nous la définissons pour utiliser une fonction d'activation linéaire et le calcul de la perte est ensuite capturé dans la fonction de perte, où nous avons le paramètre "from_logits=True". Cette implémentation peut être moins lisible, mais elle entraîne moins d'erreurs d'arrondi numérique et devrait être utilisée pour des calculs plus précis dans TensorFlow.

Il est important de noter que en utilisant cette approche, nous avons modifié le réseau neuronal pour utiliser une fonction d'activation linéaire plutôt qu'une fonction d'activation softmax. Cela signifie que la couche finale du réseau neuronal ne produit plus de probabilités, mais plutôt z_1 à z_10. Dans le cas de la régression logistique, nous devons également changer le code pour prendre la valeur de sortie et la mapper à travers la fonction

Le problème avec la classification multi-label

Lorsqu'il s'agit de construire un réseau neuronal pour la classification d'images, il y a deux principaux types de problèmes à considérer: la classification multi-classes et la classification multi-étiquettes.

Dans un problème de classification multi-classes, il y a une seule étiquette associée à chaque image d'entrée. Par exemple, dans un problème de classification de chiffres manuscrits, l'étiquette cible (Y) est un seul nombre, même si ce nombre peut prendre 10 valeurs différentes possibles.

D'autre part, dans un problème de classification multi-étiquettes, il peut y avoir plusieurs étiquettes associées à chaque image d'entrée.

Par exemple, dans une application de voiture autonome, lorsqu'une photo de ce qui se trouve devant la voiture est donnée, nous pouvons poser des questions comme: "Y a-t-il une voiture ou au moins une voiture? Y a-t-il un bus? Y a-t-il un piéton ou y a-t-il des piétons? " Dans ce cas, l'étiquette cible (Y) est un vecteur de trois nombres, correspondant à la présence ou non de voitures, de bus ou de piétons dans l'image.

Une façon de construire un réseau neuronal pour la classification multi-étiquettes est de le traiter comme trois problèmes d'apprentissage automatique séparés.

Par exemple, nous pourrions construire un réseau neuronal pour décider s'il y a des voitures, un deuxième pour détecter les bus et un troisième pour détecter les piétons. Cependant, une autre façon de le faire est de former un seul réseau neuronal pour détecter simultanément les trois éléments: voitures, bus et piétons.

Pour cela, notre architecture de réseau neuronal aurait une couche d'entrée, suivie d'une ou plusieurs couches cachées et une couche de sortie finale avec plusieurs nœuds. Comme nous résolvons trois problèmes de classification binaire, nous pouvons utiliser une fonction d'activation sigmoïde pour chacun de ces nœuds de sortie. La sortie finale du réseau serait un vecteur de trois nombres.

L'algorithme d'Adam

Adam signifie Estimation de Moment Adaptatif et c'est un algorithme d'optimisation populaire utilisé dans l'apprentissage profond. Contrairement aux algorithmes d'optimisation traditionnels qui utilisent un taux d'apprentissage global unique, Adam utilise des taux d'apprentissage différents pour chaque paramètre individuel du modèle. Cela permet à l'algorithme de s'adapter au comportement spécifique de chaque paramètre.

L'intuition derrière l'algorithme Adam est que si un paramètre semble continuer à se déplacer dans la même direction, le taux d'apprentissage pour ce paramètre doit être augmenté pour aller plus vite dans cette direction. Inversement, si un paramètre continue à osciller d'avant en arrière, le taux d'apprentissage pour ce paramètre doit être réduit pour éviter qu'il ne continue à osciller.

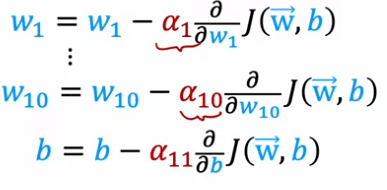
Les détails de la façon dont Adam adapte le taux d'apprentissage pour chaque paramètre sont un peu compliqués, mais il est implémenté en code en utilisant l'optimiseur tf.keras.optimizers.Adam. L'algorithme d'optimisation Adam a besoin d'un taux d'apprentissage initial par défaut, et dans cet exemple, il est défini à 10^-3. Cependant, lors de l'utilisation de l'algorithme Adam en pratique, il est judicieux d'essayer différentes valeurs pour le taux d'apprentissage initial pour voir lequel donne les meilleures performances.

Comparé à l'algorithme de descente de gradient original, l'algorithme Adam est plus robuste face au choix exact du taux d'apprentissage et fonctionne généralement beaucoup plus rapidement. Il est devenu un standard de facto dans la façon dont les praticiens entraînent leurs réseaux de neurones et si vous devez décider quel algorithme d'optimisation utiliser, le choix sûr serait d'utiliser l'algorithme d'optimisation Adam.

Convolutional layer

Dans cet article, nous allons examiner un type différent de couche dans les réseaux de neurones appelé couche de convolution. Ce type de couche est utilisé dans certaines applications car il peut accélérer le calcul et faire en sorte qu'un réseau de neurones nécessite moins de données d'entraînement ou soit moins sujet à l' surapprentissage.

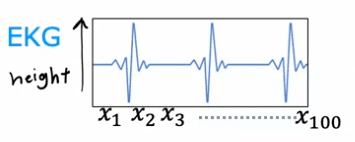
Une couche de convolution est une couche où chaque neurone ne regarde qu'une région de l'image d'entrée, plutôt que tous les pixels. Cela peut être illustré avec un exemple de classification des signaux EKG. Dans cet exemple, la première unité cachée dans une couche de convolution ne regarderait qu'une petite fenêtre du signal EKG, comme X1 à X20. La seconde unité regarderait une fenêtre différente, comme X11 à X30, etc. Il s'agit d'une couche de convolution car ces unités dans cette couche ne regardent qu'une fenêtre limitée de l'entrée.

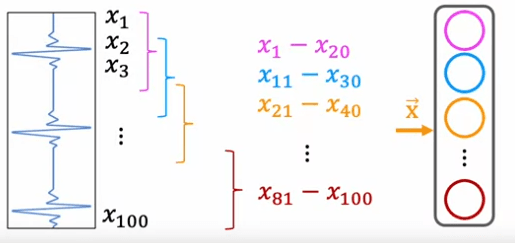
Il est important de noter que la prochaine couche peut également être une couche de convolution. Dans la seconde couche cachée, la première unité peut ne regarder que les cinq premières activations de la couche précédente, la seconde unité peut regarder un autre cinq nombres, et la troisième et dernière unité cachée de cette couche ne regardera qu'un certain ensemble d'activations. Enfin, ces activations sont entrées dans une unité sigmoïde qui regarde toutes ces valeurs afin de faire une classification binaire concernant la présence ou l'absence de maladie cardiaque.

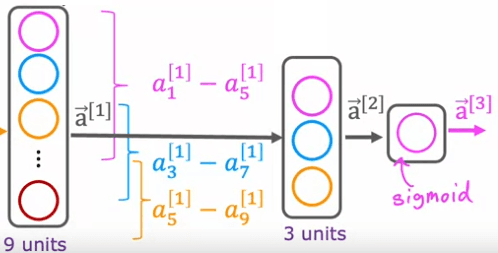
Dans cet exemple, le réseau de neurones a une première couche cachée qui est une couche de convolution, une deuxième couche cachée qui est également une couche de convolution, et une couche de sortie qui est une couche sigmoïde. Il y a de nombreux choix architecturaux lors de l'utilisation de couches de convolution, tels que la taille de la fenêtre d'entrées que doit regarder un neurone unique et le nombre de neurones que la couche doit avoir. En choisissant ces paramètres architecturaux efficacement, vous pouvez créer de nouvelles versions de réseaux de neurones qui peuvent être encore plus efficaces que les couches denses pour certaines applications.

En résumé, les couches de convolution et les réseaux de neurones convolutionnels sont un type différent de couche.

Evaluer un modèle

Apprendre à prédire les prix de l'immobilier en fonction de la taille peut être une tâche difficile. Pour faciliter cela, un modèle peut être entraîné pour prédire les prix de l'immobilier en fonction de la taille x. Un exemple de ceci est un polynôme de quatrième degré, qui inclut des caractéristiques telles que :

x1	Size
x2	Numbers of bedrooms
x3	Numbers of floors
x4	Age of home in years

Ce modèle peut bien s'adapter aux données d'entraînement, mais il peut ne pas généraliser bien aux nouveaux exemples qui ne font pas partie de l'ensemble d'entraînement.

Lors de la prédiction des prix, il peut être difficile de savoir si un modèle fonctionne bien, surtout lorsqu'il y a plus d'une ou deux caractéristiques. Une technique qui peut être utilisée pour évaluer les performances d'un modèle consiste à diviser l'ensemble d'entraînement en deux sous-ensembles : un ensemble d'entraînement et un ensemble de test. Les paramètres du modèle peuvent être entraînés sur l'ensemble d'entraînement et ensuite testés sur l'ensemble de test.

Par exemple pour un dataset de 10 exemples :

Size	Prices
2104	400
1600	330
2400	369
1416	232
3000	540
1985	300
1534	315
1427	199
1380	212
1494	243

Apprendre à prédire les prix de l'immobilier en fonction de la taille peut être une tâche difficile. Pour vous aider, un modèle peut être formé pour prédire les prix de l'immobilier en fonction de la taille x. Un exemple de ceci est un polynôme du quatrième ordre, qui inclut des caractéristiques telles que:

Ce modèle peut s'adapter bien aux données d'entraînement, mais il peut ne pas généraliser bien aux nouveaux exemples qui ne sont pas dans l'ensemble d'entraînement.

Lors de la prédiction des prix, il peut être difficile de dire si un modèle fonctionne bien, surtout lorsqu'il y a plus d'une ou deux caractéristiques. Une technique qui peut être utilisée pour évaluer les performances d'un modèle est de diviser l'ensemble d'entraînement en deux sous-ensembles: un ensemble d'entraînement et un ensemble de test. Les paramètres du modèle peuvent être formés sur l'ensemble d'entraînement et ensuite testés sur l'ensemble de test.

Il peut être divisé en un ensemble d'entraînement de 70% des données et un ensemble de test de 30% des données. Dans cet exemple, l'ensemble d'entraînement aurait sept exemples et l'ensemble de test aurait trois exemples.

mtrain = no.d'exemples d'entraînement = 7 mtest = ensemble de test = 3

Pour entraîner un modèle en utilisant la régression linéaire avec une erreur de carrée coût, les paramètres peuvent être ajustés en minimisant la fonction de coût, qui inclut un terme de régularisation. Les performances du modèle peuvent ensuite être évaluées en calculant l'erreur moyenne sur l'ensemble de test, également connue sous le nom de J test de w,b. Cela est fait en calculant l'erreur de carrée sur chaque exemple de test et en la moyennant sur le nombre d'exemples de test.

Dans les problèmes de classification, J train et J test peuvent être définis de manière légèrement différente. Au lieu d'utiliser la perte logistique pour calculer l'erreur de test et l'erreur d'entraînement, une méthode plus couramment utilisée est de mesurer la fraction de l'ensemble de test et de l'ensemble d'entraînement que l'algorithme a mal classifiée. Par exemple, dans un problème de classification de chiffres manuscrits 0 ou 1, J test serait la fraction de l'ensemble de test où 0 a été classifié comme 1 ou 1 a été classifié comme 0. De manière similaire, J train serait la fraction de l'ensemble d'entraînement qui a été mal classifiée.

Il est important de noter que le taux d'erreur de test est toujours supérieur au taux d'erreur d'entraînement. C'est parce que le modèle est entraîné à s'adapter aux données d'entraînement le mieux possible, et il se comportera toujours mieux sur les données sur lesquelles il a été entraîné que sur de nouvelles données non vues.

En conclusion, en divisant un jeu de données en un jeu d'entraînement et un jeu de test, et en calculant à la fois J tests et J train, nous pouvons évaluer de manière systématique comment fonctionne l'algorithme d'apprentissage. Cette procédure permet de mesurer les performances sur le jeu de test et sur le jeu d'entraînement, et peut être utilisée comme une étape pour choisir automatiquement le modèle approprié pour une application donnée de l'apprentissage automatique. C'est une étape cruciale dans l'évaluation et l'amélioration des performances des modèles d'apprentissage automatique.

Model selection

Il est important de noter que l'erreur d'entraînement d'un modèle d'apprentissage automatique n'est pas toujours un bon indicateur de la façon dont il se comportera sur de nouveaux exemples non vus. Dans cet article, nous explorerons comment l'utilisation d'un jeu de test peut nous aider à choisir un modèle pour une application d'apprentissage automatique donnée.

Imaginons un scénario où nous essayons de adapter une fonction pour prédire les prix de l'immobilier à l'aide d'un modèle linéaire, tel qu'un polynôme du premier ordre. Nous adaptons ce modèle à notre ensemble d'entraînement et obtenons les paramètres w et b. Nous pouvons alors calculer l'erreur du jeu de test, J_test, pour estimer à quel point le modèle généralisera bien aux nouvelles données.

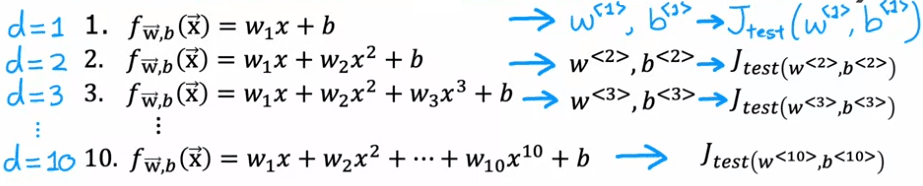
Maintenant, disons que nous envisageons également de adapter un polynôme du second ordre et un polynôme du troisième ordre, et que nous continuons ce processus jusqu'à un polynôme du dixième ordre. Nous obtiendrons J_test pour chacun de ces modèles, ce qui nous donnera une idée de la performance de chacun. Une procédure que nous pourrions essayer est de regarder tous ces J_tests et de voir lequel donne la valeur la plus basse. Par exemple, si nous constatons que J_test pour le polynôme de cinquième degré (d = 5) se révèle être le plus bas, nous pourrions décider de choisir ce modèle pour notre application.

the cross-validation

Cependant, cette procédure est défectueuse. L'utilisation du jeu de test pour choisir le paramètre d (dans ce cas, le degré du polynôme) peut entraîner une estimation trop optimiste de l'erreur de généralisation. Pour éviter ce problème, nous pouvons modifier la procédure d'entraînement et de test en divisant nos données en trois sous-ensembles : l'ensemble d'entraînement, l'ensemble de validation croisée et l'ensemble de test.

Size	Prices
2104	400
1600	330
2400	369
1416	232
3000	540
1985	300
1534	315
1427	199
1380	212
1494	243

Par exemple, nous pourrions utiliser 60% de nos données pour l'ensemble d'entraînement, 20% pour l'ensemble de validation croisée et les 20% restants pour l'ensemble de test. Nous pouvons ensuite utiliser l'ensemble de validation croisée pour choisir le meilleur modèle et rapporter l'erreur de l'ensemble de test comme une estimation de la performance du modèle sur de nouvelles données. En utilisant cette procédure modifiée, nous pouvons éviter le problème de choisir un modèle qui ne peut pas bien fonctionner sur de nouvelles données.

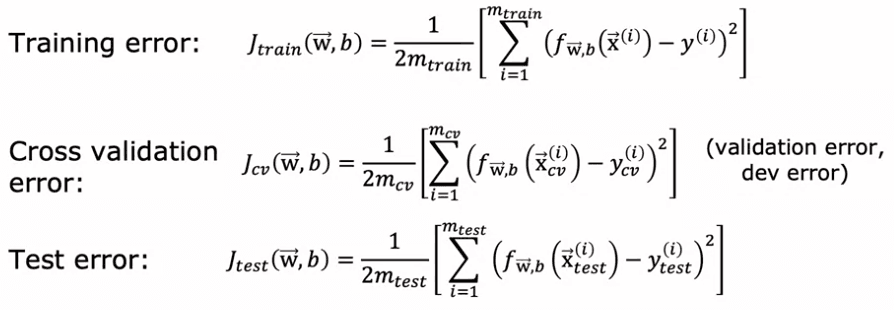
La façon dont nous allons modifier la procédure est de ne pas diviser vos données en deux sous-ensembles uniquement, l'ensemble d'entraînement et l'ensemble de test, mais de les diviser en trois sous-ensembles différents, que nous appellerons l'ensemble d'entraînement, l'ensemble de validation croisée et l'ensemble de test. En utilisant notre exemple précédent de ces 10 exemples d'entraînement, nous pourrions les diviser en mettant 60 pour cent des données dans l'ensemble d'entraînement et la notation que nous utiliserons pour la partie de l'ensemble d'entraînement sera la même que précédemment, sauf que maintenant M train, le nombre d'exemples d'entraînement sera de six et nous pourrions mettre 20 pour cent des données dans l'ensemble de validation croisée et une notation que je vais utiliser est x_cv of one, y_cv of one pour le premier exemple de validation croisée. Donc cv signifie validation croisée, jusqu'à x_cv de m_cv et y_cv de m_cv. Où ici, m_cv égal 2 dans cet exemple, est le nombre d'exemples de validation croisée. Enfin, nous avons l'ensemble de test, comme d'habitude, donc x1 à x m tests et y1 à y m tests. L'ensemble de test sera de la même taille que l'ensemble de validation croisée, soit 20 pour cent des données totales.

Maintenant, avec ce nouveau découpage en trois de nos données, nous pouvons utiliser l'ensemble d'entraînement pour ajuster notre modèle et l'ensemble de validation croisée pour choisir le meilleur modèle. En d'autres termes, nous pouvons utiliser l'ensemble de validation croisée pour choisir la meilleure valeur de d, le degré du polynôme. Nous pouvons essayer de faire l'ajustement d'un polynôme de premier ordre et obtenir J_cv^1, puis essayer de faire l'ajustement d'un polynôme de deuxième ordre et obtenir J_cv^2, et ainsi de suite, jusqu'à un polynôme de dixième ordre, et obtenir J_cv^10. A partir de ces valeurs, nous pouvons choisir la valeur de d qui nous donne le plus petit J_cv. Disons que nous choisissons d=5, alors nous pouvons utiliser l'ensemble de test pour obtenir une estimation de l'erreur de généralisation, J_test^5. Cette estimation de l'erreur de généralisation est moins susceptible d'être trop optimiste car nous n'avons pas utilisé l'ensemble de test pour choisir la valeur de d.

En résumé, en utilisant un découpage en trois de nos données avec un ensemble d'entraînement, un ensemble de validation croisée et un ensemble de test, nous pouvons choisir le meilleur modèle sans biaiser notre estimation de l'erreur de généralisation. L'ensemble d'entraînement est utilisé pour ajuster le modèle, l'ensemble de validation croisée est utilisé pour choisir le meilleur modèle et l'ensemble de test est utilisé pour estimer l'erreur de généralisation. C'est une manière plus robuste de sélectionner un modèle pour les applications d'apprentissage automatique.